
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение уравнений и неравенств графическим способом
Пример 1. Графически решить уравнение: 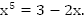
Решение:
Построим графики функций 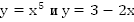 (Рис. 1).
(Рис. 1).
Графиком функции 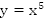 является парабола, проходящая через точки
является парабола, проходящая через точки 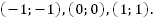
График функции 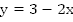 – прямая, построим её по таблице.
– прямая, построим её по таблице.
| 
| |
|
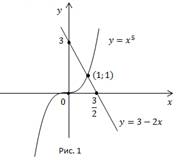
Графики пересекаются в точке 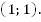 Других точек пересечения нет, т. к. функция
Других точек пересечения нет, т. к. функция 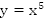 монотонно возрастает, функция
монотонно возрастает, функция 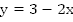 монотонно убывает, а, значит, их точка пересечения является единственной.
монотонно убывает, а, значит, их точка пересечения является единственной.
Ответ: 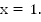
Пример 2. Решить неравенство
a. 
b. 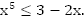
Решение:
a. Чтобы выполнялось неравенство, график функции 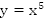 должен располагаться над прямой
должен располагаться над прямой 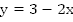 (Рис. 1). Это выполняется при
(Рис. 1). Это выполняется при 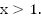
b. В этом случае, наоборот, парабола 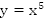 должна находиться под прямой. Это выполняется при
должна находиться под прямой. Это выполняется при 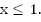
Ответ:
a. 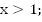
b. 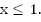
Пример 3. Решить неравенство 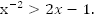 Мы знаем х -2=
Мы знаем х -2= 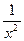
Решение: Построим графики функций 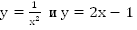 (Рис. 2).
(Рис. 2).
Для этого составим таблицы у= 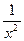
| х | -2 | -1 | - ½ | -1/3 |
| у | ¼ |
| х | ½ | 1/3 | |||
| у | 4 | ¼ |
у=2х-1
| х | ||
| у | -1 |
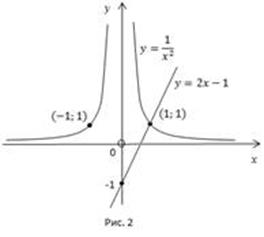
Найдем корень уравнения 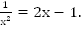 При
При 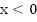 нет решений. При
нет решений. При 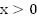 существует одно решение
существует одно решение 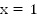 .
.
Чтобы выполнялось неравенство 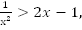 гипербола
гипербола 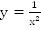 должна располагаться над прямой
должна располагаться над прямой 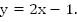 Это выполняется при
Это выполняется при 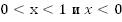 .
.
Ответ: 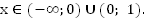
Пример 4. Решить графически неравенство:
a. 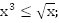
b. 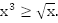
Решение.
Область определения: 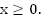
Построим графики функций 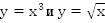 для
для 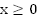 (Рис. 3).
(Рис. 3).
у=х3
| х | ½ | |||
| у | 1/8 |
y= 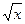
| х | ||||
| у |
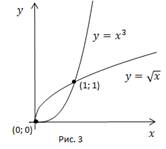
a. График функции  должен располагаться под графиком
должен располагаться под графиком 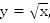 это выполняется при
это выполняется при 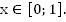
b. График функции  расположен над графиком
расположен над графиком 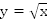 при
при 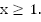 Но т. к. в условии имеем нестрогий знак, важно не потерять изолированный корень
Но т. к. в условии имеем нестрогий знак, важно не потерять изолированный корень 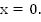
Ответ:
a. 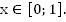
b. 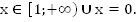
Решить уравнение
(1/2)x=x+3
1. Составим таблицы и построим графики показательной и линейной функций y=(1/2)x и y=x+3.
Составим таблицу и построим график показательной функции y=(1/2)x
.
| х | -3 | -2 | -1 | ||||
| у | ½ | ¼ | 1/8 |
Составим таблицу и построим график линейной функции y=x+3.
| х | ||
| у |
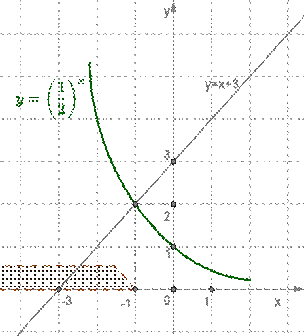
х=-1
Решите неравенство графическим способом:
х2 – х – 2 ≥ 0.
РЕШЕНИЕ:
Представим такое неравенство в виде
х2 ≥ х + 2.
В одной и той же системе координат построим графики функций
у1 = х2 (парабола)
| х | -3 | -2 | -1 | ||||
| у |
у2 = х + 2 (прямая линия).
| х | ||
| у |
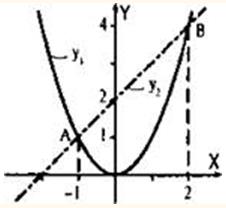
Найдём абсциссы точек пересечения этих графиков. Приравняем правые части функций и получим уравнение:
х2 = х + 2
или
х2 – х – 2 = 0.
Корни этого квадратного уравнения
х1 = –1 и х2 = 2.
Поэтому такие графики пересекаются в двух точках А и В,
абсциссы которых, соответственно, равны
х1 = –1 и х2 = 2.
Неравенству
х2 ≥ х + 2
или
у1 ≥ у2
удовлетворяют те значения х, при которых значения первой функции больше или равны значениям второй функции, то есть при которых график первой функции расположен выше или на уровне второй функции. Из рисунка видно, что такими значениями являются все числа из промежутков
х1 ≤ –1 и х2 ≥ 2.
Этот способ оказывается более полезным при решении сложных неравенств (кубических неравенств, неравенств с модулем и так далее).
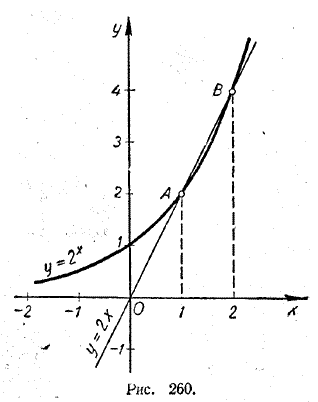
Решить уравнение
2х = 2х.
На одном и том же чертеже (рис. 260) построим графики двух функций: у = 2х и у = 2х. Эти графики пересекаются в двух точках: А с абсциссой 1 и В с абсциссой 2. Поэтому данное уравнение имеет два корня: х = 1 и х =2.
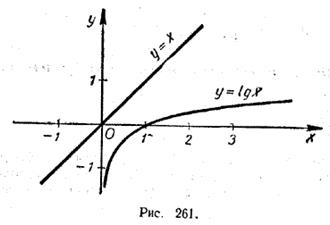
Пример 2. Решить уравнение
lg х = х.
Графики функций y = lg х и y = x (рис. 261) не пересекаются друг с другом. Поэтому данное уравнение не имеет корней.
у=lgx x> 0
| х | 
| ||
| у | =1 |
y = x
| х | ||
| у |
Решений нет
Решите самостоятельно:
а) 2х = х + 2; в) 2х = x2; д) log2 x = x/2;
б) 3х > 3х; г) log2 x< x-1; е) log2 (х + 3) 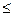 3 — х
3 — х
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|