
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
10 класс Алгебра Дата_07.02.22_
10 класс Алгебра Дата_07. 02. 22_
" Логарифмическая функция, её свойства и график "
1. Посмотрите видео https: //www. youtube. com/watch? v=6YjsFYcPusc
2. Запишите определение и свойства логарифмической функции.
3. Разберите примеры.
Выполните домашнее задание: §18, №318(1, 2), 325(1, 2), 327(1), 328(1, 3).
Запомните! Функцию 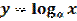 , где
, где 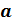 — заданное число,
— заданное число, 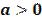 и
и 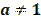 , называют логарифмической.
, называют логарифмической.
Основные свойства логарифмической функции.
1. Область определения логарифмической функции — множество всех положительных чисел.
2. Множество значений логарифмической функции — множество  всех действительных чисел.
всех действительных чисел.
3. Логарифмическая функция не является ограниченной.
4. Логарифмическая функция 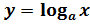 является возрастающей на промежутке
является возрастающей на промежутке 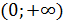 , если
, если 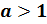 , и убывающей, если
, и убывающей, если 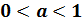 .
.
Хотелось бы отметить, что справедливыми будут и обратные утверждения:
если 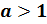 и
и 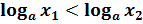 , где
, где 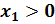 ,
, 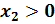 , то
, то 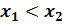 ;
;
если 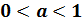 и
и 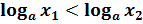 , где
, где 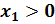 ,
, 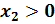 , то
, то 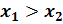 .
.
5. Если 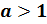 , то функция
, то функция 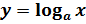 принимает положительные значения при
принимает положительные значения при 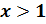 , отрицательные при
, отрицательные при 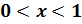 .
.
Если 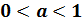 , то функция
, то функция 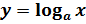 принимает положительные значения при
принимает положительные значения при 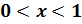 , отрицательные при
, отрицательные при 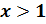 .
.
Как же будет выглядеть график такой функции?
Итак, давайте построим графики функций 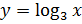 (здесь
(здесь  ) и
) и 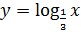 (здесь
(здесь 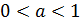 ).
).
Для этого, как обычно, найдём сначала координаты некоторых точек графика и заполним таблицу значений функций.

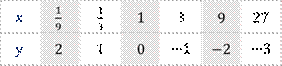
Отметим эти точки на координатной плоскости и соединим их.

Получившиеся кривые являются графиками функций 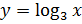 и
и 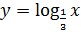 .
.
Заметим, что значение равное 0 логарифмическая функция принимает в точке 1. Это следует из того, что 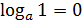 при любом
при любом 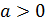 , так как
, так как 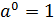 .
.
Ось О 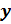 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции 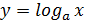 .
.
При решении уравнений часто используется следующая теорема:
Теорема: если 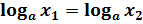 , где
, где 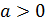 ,
,  ,
, 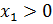 ,
, 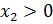 , то
, то 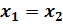 .
.
Логарифмическая функция 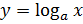 и показательная функция
и показательная функция 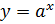 , где
, где 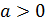 и
и  взаимно обратны.
взаимно обратны.
А теперь давайте приступим к практической части нашего урока.


|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|