
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Неопределенный интеграл. Подробные примеры решений
На данном уроке мы начнём изучение темы Неопределенный интеграл, а также подробно разберем примеры решений простейших (и не совсем) интегралов.
В этой связи нам потребуются следующие методические материалы: Таблица производных и Таблица интегралов. Справочные пособия можно открыть, закачать или распечатать на странице Математические формулы и таблицы.
В чем сложность изучения неопределенных интегралов? Если в производных имеют место строго 5 правил дифференцирования, таблица производных и довольно четкий алгоритм действий, то в интегралах всё иначе. Существуют десятки способов и приемов интегрирования.
Коль скоро способов решения существует очень много, то, с чего же начать изучение неопределенных интегралов чайнику? В интегральном исчислении существуют, на мой взгляд, три столпа или своеобразная «ось», вокруг которой вращается всё остальное. В первую очередь следует хорошо разобраться в простейших интегралах. Потом нужно детально проработать урок Метод замены в неопределенном интеграле. Может быть, даже самая важная статья из всех статей, посвященных интегралам. И, в-третьих, обязательно следует ознакомиться с методом интегрирования по частям, поскольку с помощью него интегрируется обширный класс функций.
Знания и навыки по неопределенному интегралу потребуются в дальнейшей учебе, в частности, при изучении определенного интеграла, несобственных интегралов, дифференциальных уравнений. Необходимость взять интеграл возникает даже в теории вероятностей. Чем больше интегралов различных типов вы прорешаете, тем легче будет дальнейшая жизнь.
Итак, начинаем с простого. Посмотрим на таблицу интегралов. Как и в производных, мы замечаем несколько правил интегрирования и таблицу интегралов от некоторых элементарных функций. Нетрудно заметить, что любой табличный интеграл (да и вообще любой неопределенный интеграл) имеет вид:
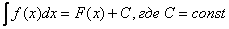
Сразу разбираемся в обозначениях и терминах:
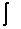 – значок интеграла.
– значок интеграла.
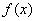 – подынтегральная функция (пишется с буквой «ы»).
– подынтегральная функция (пишется с буквой «ы»).
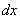 – значок дифференциала. При записи интеграла и в ходе решения важно не терять данный значок. Заметный недочет будет.
– значок дифференциала. При записи интеграла и в ходе решения важно не терять данный значок. Заметный недочет будет.
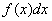 – подынтегральное выражение или «начинка» интеграла.
– подынтегральное выражение или «начинка» интеграла.
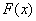 – первообразная функция.
– первообразная функция.
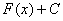 – множество первообразных функций. Не нужно сильно загружаться терминами, самое важное, что в любом неопределенном интеграле к ответу приплюсовывается константа
– множество первообразных функций. Не нужно сильно загружаться терминами, самое важное, что в любом неопределенном интеграле к ответу приплюсовывается константа 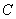 .
.
Решить интеграл – это значит найти определенную функцию 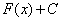 , пользуясь некоторыми правилами, приемами и таблицей.
, пользуясь некоторыми правилами, приемами и таблицей.
Еще раз посмотрим на запись:

Посмотрим в таблицу интегралов.
Что происходит? Левые части 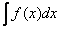 у нас превращаются в другие функции:
у нас превращаются в другие функции: 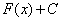 .
.
Упростим наше определение.
Решить неопределенный интеграл 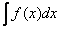 – это значит ПРЕВРАТИТЬ его в определенную функцию
– это значит ПРЕВРАТИТЬ его в определенную функцию 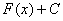 , пользуясь некоторыми правилами, приемами и таблицей.
, пользуясь некоторыми правилами, приемами и таблицей.
Возьмем, например, табличный интеграл  . Что произошло?
. Что произошло? 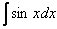 превратился в функцию
превратился в функцию 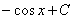 .
.
Как и в случае с производными, для того, чтобы научиться находить интегралы, не обязательно быть в курсе, что такое интеграл, первообразная функция с теоретической точки зрения. Достаточно просто осуществлять превращения по некоторым формальным правилам. Так, в случае  совсем не обязательно понимать, почему интеграл
совсем не обязательно понимать, почему интеграл 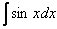 превращается именно в
превращается именно в 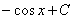
Так как дифференцирование и интегрирование – противоположные операции, то для любой первообразной, которая найдена правильно, справедливо следующее:
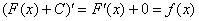
Иными словами, если продифференцировать правильный ответ, то обязательно должна получиться исходная подынтегральная функция.
Вернемся к тому же табличному интегралу  .
.
Убедимся в справедливости данной формулы. Берем производную от правой части:
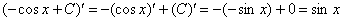 – исходная подынтегральная функция.
– исходная подынтегральная функция.
Вот, кстати, стало понятнее, почему к функции 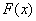 всегда приписывается константа
всегда приписывается константа 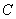 . При дифференцировании константа всегда превращается в ноль.
. При дифференцировании константа всегда превращается в ноль.
Решить неопределенный интеграл – это значит найти множество всех первообразных, а не какую-то одну функцию. В рассматриваемом табличном примере  ,
, 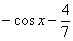 ,
, 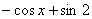 ,
, 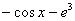 и т. д. – все эти функции являются решением интеграла
и т. д. – все эти функции являются решением интеграла 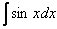 . Решений бесконечно много, поэтому записывают коротко:
. Решений бесконечно много, поэтому записывают коротко: 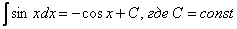
Таким образом, любой неопределенный интеграл достаточно легко проверить (в отличие от производных, где хорошую проверку можно осуществить разве что с помощью математических программ). Это некоторая компенсация за большое количество интегралов разных видов.
Переходим к рассмотрению конкретных примеров. Начнем, как и при изучении производной,
с двух правил интегрирования, которые также называют свойствами линейности неопределенного интеграла:
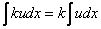 – постоянный множитель можно (и нужно) вынести за знак интеграла.
– постоянный множитель можно (и нужно) вынести за знак интеграла.
 – интеграл от алгебраической суммы двух функций равен алгебраической сумме двух интегралов от каждой функции в отдельности. Данное свойство справедливо для любого количества слагаемых.
– интеграл от алгебраической суммы двух функций равен алгебраической сумме двух интегралов от каждой функции в отдельности. Данное свойство справедливо для любого количества слагаемых.
Как видите, правила, в принципе, такие же, как и для производных.
Пример 1
Найти неопределенный интеграл. Выполнить проверку.
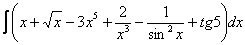
Решение: Удобнее переписать его на бумагу.

(1) Применяем правило  . Не забываем записать значок дифференциала
. Не забываем записать значок дифференциала 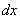 под каждым интегралом. Почему под каждым?
под каждым интегралом. Почему под каждым? 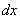 – это полноценный множитель, если расписывать решение совсем детально, то первый шаг следует записать так:
– это полноценный множитель, если расписывать решение совсем детально, то первый шаг следует записать так:

(2) Согласно правилу 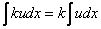 , выносим все константы за знаки интегралов. Обратите внимание, что в последнем слагаемом
, выносим все константы за знаки интегралов. Обратите внимание, что в последнем слагаемом 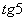 – это константа, её также выносим.
– это константа, её также выносим.
Кроме того, на данном шаге готовим корни и степени для интегрирования. Точно так же, как и при дифференцировании, корни надо представить в виде  . Корни и степени, которые располагаются в знаменателе – перенести вверх.
. Корни и степени, которые располагаются в знаменателе – перенести вверх.
(3) Все интегралы у нас табличные. Осуществляем превращение с помощью таблицы, используя формулы: 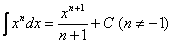 ,
, 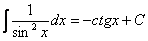 и
и  .
.
Особое внимание обращаю на формулу интегрирования степенной функции 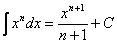 , она встречается очень часто, ее лучше запомнить. Следует отметить, что табличный интеграл
, она встречается очень часто, ее лучше запомнить. Следует отметить, что табличный интеграл  – частный случай этой же формулы:
– частный случай этой же формулы: 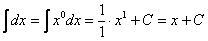 .
.
Константу 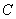 достаточно приплюсовать один раз в конце выражения (а не ставить их после каждого интеграла).
достаточно приплюсовать один раз в конце выражения (а не ставить их после каждого интеграла).
(4) Записываем полученный результат в более компактном виде, все степени вида  снова представляем в виде корней, степени с отрицательным показателем – сбрасываем обратно в знаменатель.
снова представляем в виде корней, степени с отрицательным показателем – сбрасываем обратно в знаменатель.
Проверка. Для того чтобы выполнить проверку нужно продифференцировать полученный ответ:
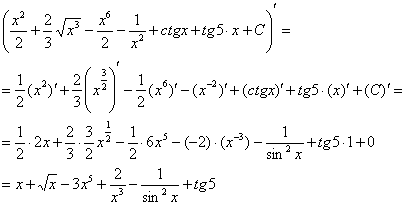
Получена исходная подынтегральная функция, значит, интеграл найден правильно. От чего плясали, к тому и вернулись. Знаете, очень хорошо, когда история с интегралом заканчивается именно так.
Время от времени встречается немного другой подход к проверке неопределенного интеграла, от ответа берется не производная, а дифференциал:
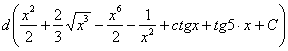
Кто с первого семестра понял, тот понял, но сейчас нам важны не теоретические тонкости, а важно то, что с этим дифференциалом дальше делать. Его необходимо раскрыть, и с формально-технической точки зрения – это почти то же самое, что найти производную. Дифференциал раскрывается следующим образом: значок 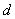 убираем, справа над скобкой ставим штрих, в конце выражения приписываем множитель
убираем, справа над скобкой ставим штрих, в конце выражения приписываем множитель 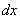 :
:
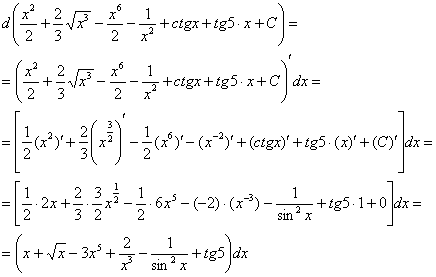
Получено исходное подынтегральное выражение, значит, интеграл найден правильно.
Второй способ проверки мне нравится меньше, так как приходится дополнительно рисовать большие скобки и тащить значок дифференциала 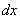 до конца проверки.
до конца проверки.
На самом деле я вообще мог умолчать о втором способе проверки. Дело не в способе, а в том, что мы научились раскрывать дифференциал. Еще раз.
Дифференциал раскрывается следующим образом:
1) значок 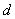 убираем;
убираем;
2) справа над скобкой ставим штрих (обозначение производной);
3) в конце выражения приписываем множитель 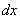 .
.
Например: 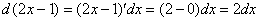
Пример 2
Найти неопределенный интеграл. Выполнить проверку.
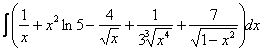
Пример 3
Найти неопределенный интеграл. Выполнить проверку.
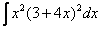
Решение: Анализируя интеграл, мы видим, что у нас произведение двух функций, да еще и возведение в степень целого выражения. К сожалению, на поприще интегральной битвы нет хороших и удобных формул для интегрирования произведения и частного  ,
,  .
.
А поэтому, когда дано произведение или частное, всегда имеет смысл посмотреть, а нельзя ли преобразовать подынтегральную функцию в сумму?
Рассматриваемый пример – тот случай, когда можно. Сначала я приведу полное решение, комментарии будут ниже.
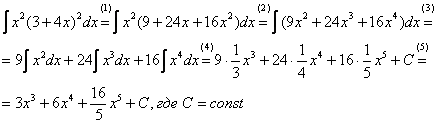
(1) Используем старую-добрую формулу квадрата суммы  , избавляясь от степени.
, избавляясь от степени.
(2) Вносим  в скобку, избавляясь от произведения.
в скобку, избавляясь от произведения.
(3) Используем свойства линейности интеграла (оба правила сразу).
(4) Превращаем интегралы по табличной формуле 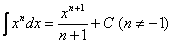 .
.
(5) Упрощаем ответ. Здесь следует обратить внимание на обыкновенную неправильную дробь 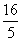 – она несократимая и в ответ входит именно в таком виде. Не нужно делить на калькуляторе
– она несократимая и в ответ входит именно в таком виде. Не нужно делить на калькуляторе 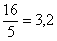 ! Не нужно представлять ее в виде
! Не нужно представлять ее в виде  !
!
Проверка:

Получена исходная подынтегральная функция, значит, интеграл найден правильно.
В ходе проверки функцию всегда желательно «упаковать» до первоначального вида, вынося в данном случае  за скобки и применяя формулу сокращенного умножения в обратном направлении:
за скобки и применяя формулу сокращенного умножения в обратном направлении: 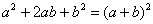
Пример 4
Найти неопределенный интеграл. Выполнить проверку.
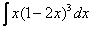
Пример 5
Найти неопределенный интеграл. Выполнить проверку.
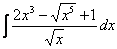
Пример 6
Найти неопределенный интеграл. Выполнить проверку.
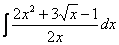
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|