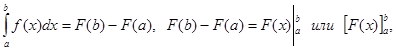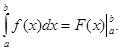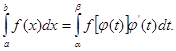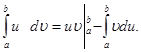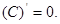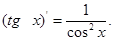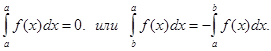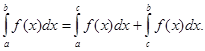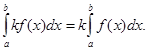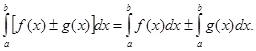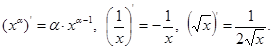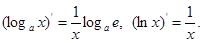- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Таблица основных интегралов:
Стр 1 из 2Следующая ⇒
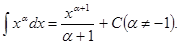
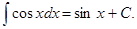
1. Производная неопр. интеграла равна подинтегральной функции; дифферинциал от неопр. интеграла равен подинтегр. выражению, т. е.
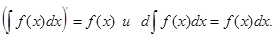
2. Неопр. интеграл от дифферинциала некоторой фун-ии равен сумме этой фун-ии и произвольной постоянной:
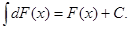
3. Постоянный множетель можно вынести из-под знака интеграла, т. е. если k=const¹ 0, то
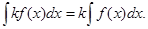
4. Неопр. интеграл от алгебраической суммы 2-х фун-ий равен алгебраической сумме интегралов от этих фун-ий в отдельности, т. е.
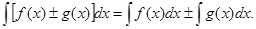
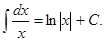
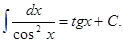
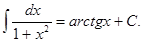
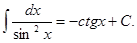
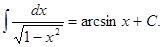
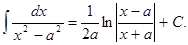

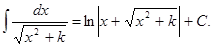
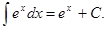
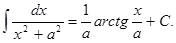
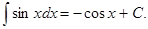

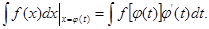
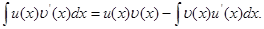 формула интегрирования по частям в неопределённом интеграле.
формула интегрирования по частям в неопределённом интеграле.