Пояснительная записка

к интерактивному плакату

« Мнемотическая схема для запоминания

тригонометрических формул и их взаимосвязей».

Тригонометрия – это такой раздел математики, в котором много формул. Некоторые студенты сразу «поднимают руки вверх», мол, «сдаюсь! » и «это мне непосильно».

Существует учительский фольклор «придумок» для запоминания этих формул, например «лошадиное правило» и т. п.

Данный плакат помогает осмыслить взаимосвязь всех формул, понять, как одно вытекает из другого. Работу с плакатом нужно начинать с первых уроков тригонометрии, постепенно открывая всё новые и новые блоки формул.

Показать, как можно за 1-5 минут заполнить бланк (прилагается), который представляет собой этот же плакат, но не заполненный.

Презентация состоит всего из двух слайдов, первый из них – титульный, а на втором нужно делать перерывы между щелчками мыши, потому что новые блоки появляются по щелчку лкм. Каждый блок формул нужно внимательно рассмотреть, выполнить вывод и т. д. Надеюсь что плакат будет вам полезен!

№ щелчка мыши	Изображение на слайде	Комментарии
1-3		Основные формулы – это главный «кирпичик» схемы. Первые три формулы – основное тригонометрическое тождество и определения тангенса и котангенса – надо выучить, а три остальные вытекают из первых. Объяснить взаимосвязь.
		Блок формул суммы (на жёлтом фоне»)- это краеугольный камень схемы, который вместе с «основными формулами» дают нам все формулы схемы. Называем этот блок «Сельскохозяйственные формулы». Почему сельскохозяйственные, станет понятно чуть позже. Для запоминания этих формул мы должны приложить максимум усилий. В качестве мнемотической подпорки используем следующие приговорки. -На что по звучанию похоже слово синус? -Сено. - Сено получают во время сенокоса. -Что делают на сенокосе? -Сено косят, косят сено. Это подсказка к тому, что при расписывании формул синусаалгебраической суммы, чередуем название функций: sin·cos? cos·sin, а знак? между произведениями совпадает со знаком между аргументами в скобках. И, вообще, для синуса со знаком проблем меньше, чем с косинусом. Для формул косинуса алгебраической суммы приговариваем: -На что по звучанию похоже слово косинус? -Косарь. -А что делает косарь? -Косит, косит – сел, сидит. Это подсказка к тому, что при расписывании формул косинусаалгебраической суммы, повторяем название функций: cos·cos ¿ sin·sin, а знак ¿ между произведениями противоположен знаку между аргументами в скобках. Для формул тангенса суммы особой приговорки нет, но помогают слова «Танец танго танцуем с каждым, подводим черту, и от целого мира (от единицы) весёлой парою отъединяемся». (вычитание от единицы)
5-7		В формулах суммы угол β заменим на α, получаем формулы двойного аргумента.
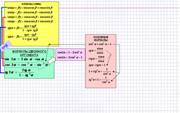
		Из формулы косинуса суммы совместно с основным тригонометрическим тождеством получаем две очень важные формулы.
		Показываем, как из предыдущих формул получаются формулы половинного аргумента.
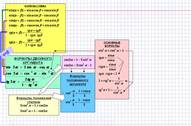
		И как из них же получаются формулы понижения степени.
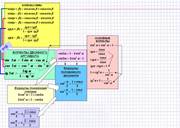
		Показываем, в каком ещё виде можно записать формулы половинного аргумента.
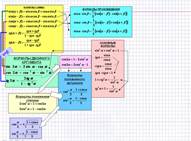
		Появляется новый блок формул: «формулы произведения». Объясняем, как получены эти формулы.
13-14		Формулы алгебраического сложения получаются из формул произведения, если мы их запишем «задом – наперёд» и переобозначим аргументы. Для суммы и разности тангенсов полезно заметить, что конструкция формулы согласована с определением тангенса: сверху - синус, снизу – косинус. Образ модели формулы – запомнить.
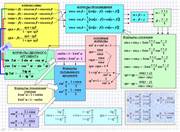
15-16		Последние два блока формул «подвальчик» рассматривают на дополнительных занятиях.