
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лабораторная работа по теме «Циклы с условием. Вложенные циклы»
Задание 1. Таблица значений функции. Составить таблицу значений функции  , для аргумента, изменяющегося на отрезке
, для аргумента, изменяющегося на отрезке 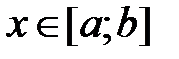 с постоянным шагом
с постоянным шагом 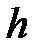 . Цикл с предусловием.
. Цикл с предусловием.
| № | Функция 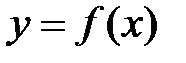
| Отрезок 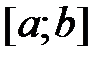
| Шаг, 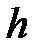
|
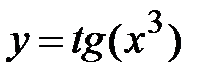
| 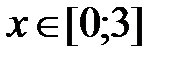
| 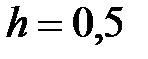
| |
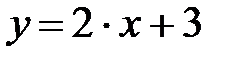
| 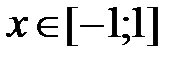
| 
| |
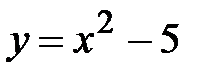
| 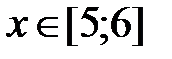
| 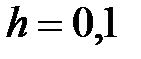
| |

| 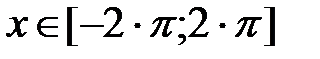
| 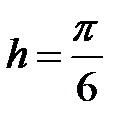
| |
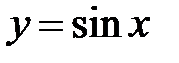
| 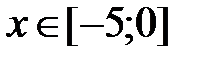
| 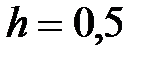
| |
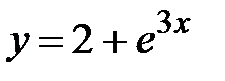
| 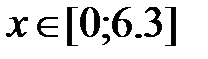
| 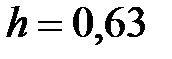
| |
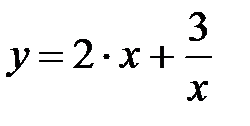
| 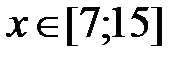
| 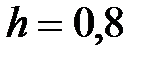
| |
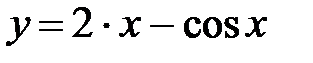
| 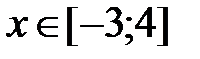
| 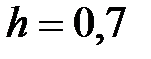
| |
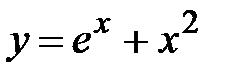
| 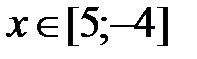
| 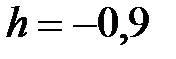
| |
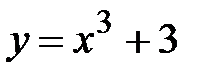
| 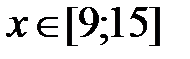
| 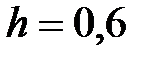
| |
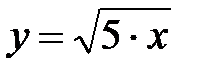
| 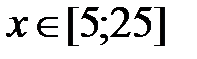
| 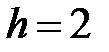
| |
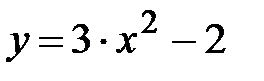
| 
| 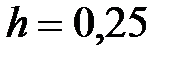
| |

| 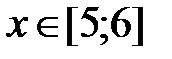
| 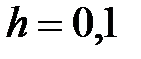
| |
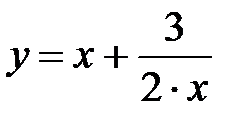
| 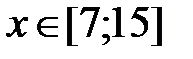
| 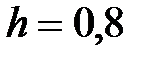
| |
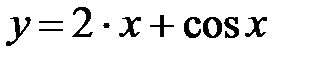
| 
| 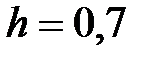
| |
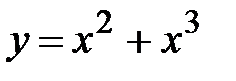
| 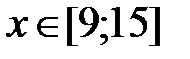
| 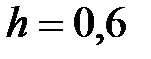
| |
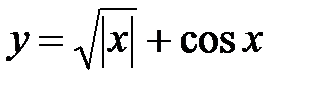
| 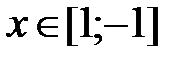
| 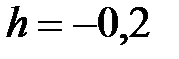
| |
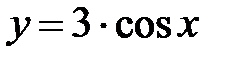
| 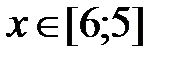
| 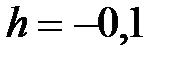
| |
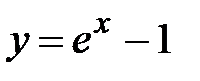
| 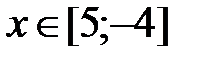
| 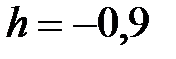
| |
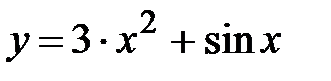
| 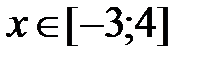
| 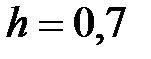
| |
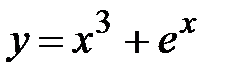
| 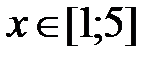
| 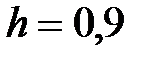
| |
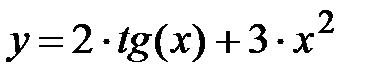
| 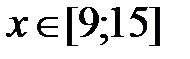
| 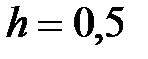
| |
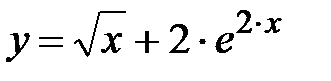
| 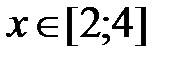
| 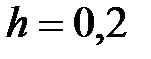
| |
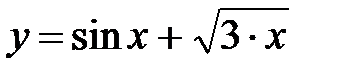
| 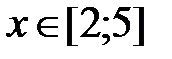
| 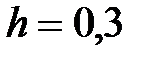
| |
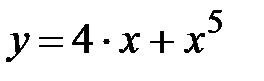
| 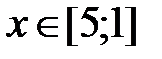
| 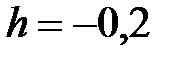
| |
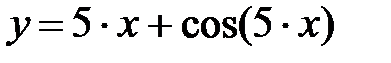
| 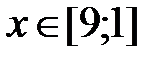
| 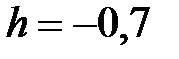
| |
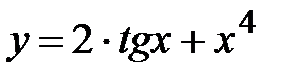
| 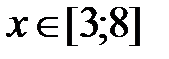
| 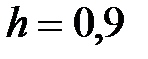
| |
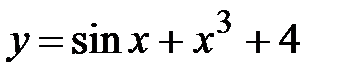
| 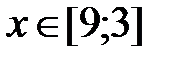
| 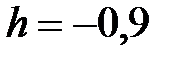
| |
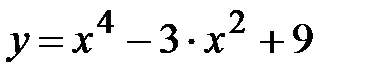
| 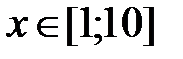
| 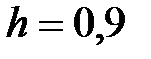
| |
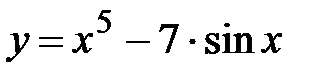
| 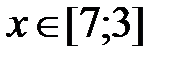
| 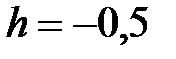
|
Задание 2. Составить программу на языке программирования Паскаль для построения таблицы значения функции на заданном отрезке. Цикл с постусловием
Вариант №1
y = 2x +3, x Є [-1; 1], h=0. 2
Вариант №2
y = x2 - 5, x Є [5; 6], h=0. 1
Вариант №3
f = cos(2x)+3, x Є [-2П; 2П], h= 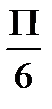
Вариант №4
y =sinx, x Є [-5; 0], h=0. 5
Вариант №5
y = 2 +e3x, x Є [0; 6. 3], h=0. 63
Вариант №6
y = 2x+ 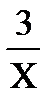 , x Є [7; 15], h=0. 8
, x Є [7; 15], h=0. 8
Вариант №7
y = 2x -cosx, x Є [-3; 4], h=0. 7
Вариант №8
y = ex +x2, x Є [5; -4], h=0. 9
Вариант №9
y = x3 +3, x Є [9; 15], h=0. 6
Вариант №10
y = 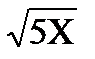 , x Є [5; 25], h=2
, x Є [5; 25], h=2
Вариант №11
y = 3x2 - 2, x Є [-5; 0], h=0. 25
Вариант №12
y = x3 +5x, x Є [5; 6], h=0. 1
Вариант №16
y = x + 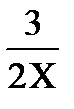 , x Є [7; 15], h=0. 8
, x Є [7; 15], h=0. 8
Вариант №17
f = 2x+cosx, x Є [-3; 4], h=0. 7
Вариант №18
y = ex - 1, x Є [5; -4], h=0. 9
Вариант №19
y = x2 +x3, x Є [9; 15], h=0. 6
Вариант №21
f = 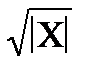 +cosx, x Є [1; -1], h= -0. 2
+cosx, x Є [1; -1], h= -0. 2
Вариант №22
f = 3cosx, x Є [6; 5], h= -0. 1
Задание № 3. Дан сходящийся бесконечный ряд с общим членом ряда  . Вычислить сумму
. Вычислить сумму 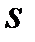 первых членов ряда, считая последним тот член ряда, абсолютное значение которого не превосходит величины
первых членов ряда, считая последним тот член ряда, абсолютное значение которого не превосходит величины 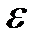 . Вывести значение
. Вывести значение 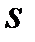 на экран.
на экран.
| № | Общий член ряда, 
| Сумма, 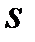
| Точность, 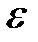
|
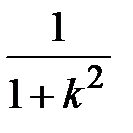
| 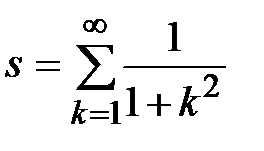
| 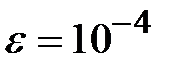
| |
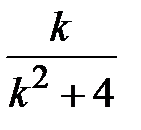
| 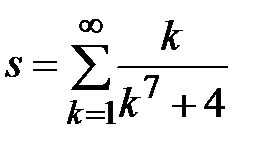
| 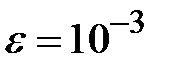
| |

| 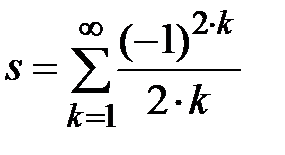
| 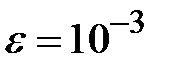
| |
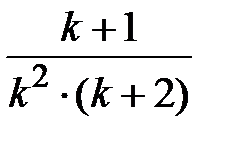
| 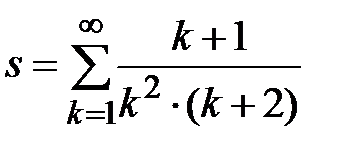
| 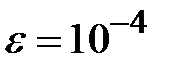
| |
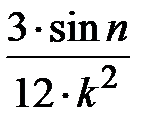
| 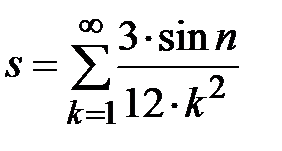
| 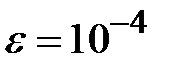
| |
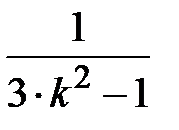
| 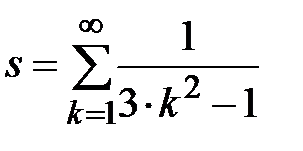
| 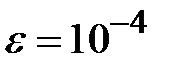
| |
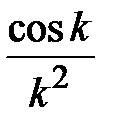
| 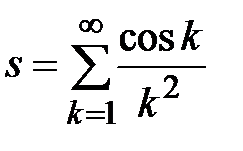
| 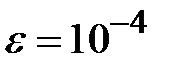
| |
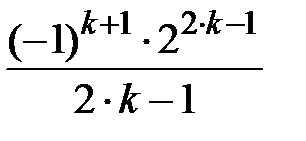
| 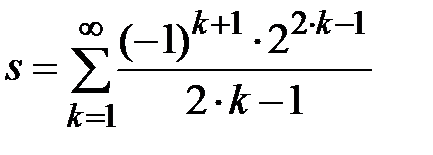
| 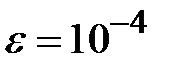
| |
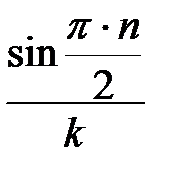
| 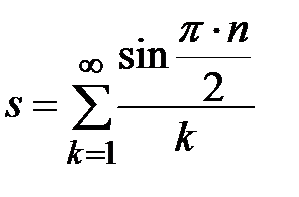
| 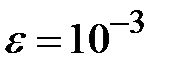
| |
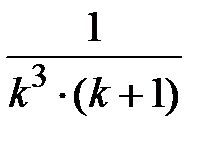
| 
| 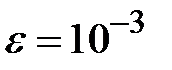
| |
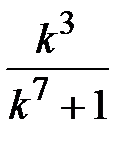
| 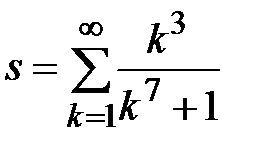
| 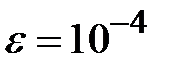
| |
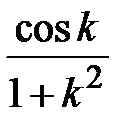
| 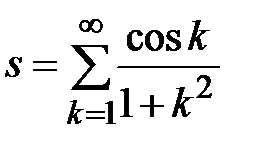
| 
| |
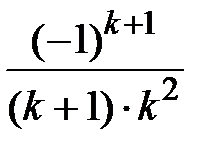
| 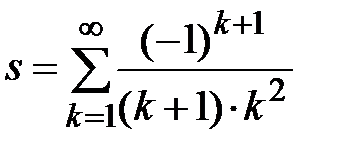
| 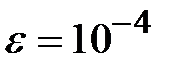
| |
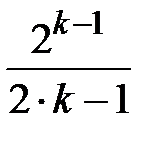
| 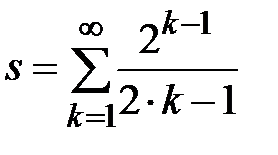
| 
| |
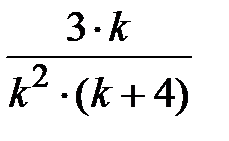
| 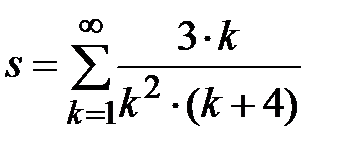
| 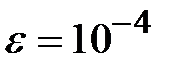
| |
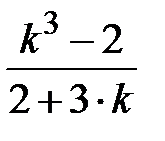
| 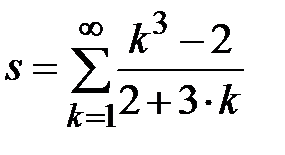
| 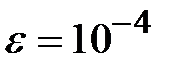
| |

| 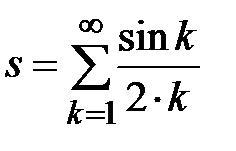
| 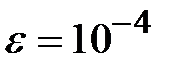
| |
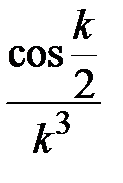
| 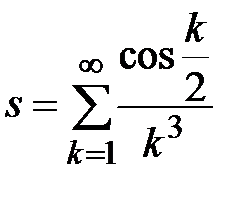
| 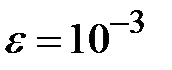
| |
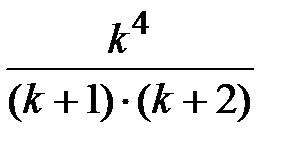
| 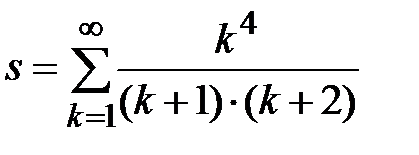
| 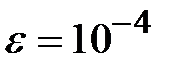
| |
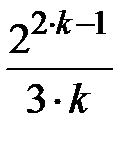
| 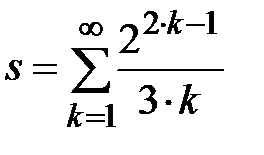
| 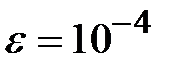
| |
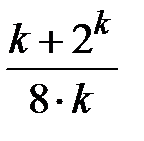
| 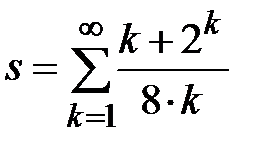
| 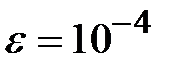
| |

| 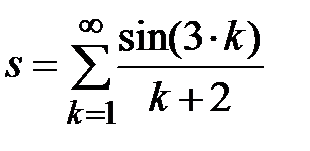
| 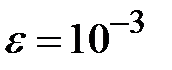
| |
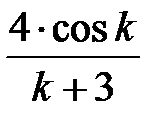
| 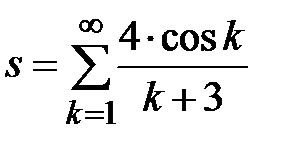
| 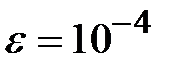
| |

| 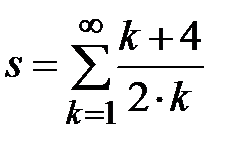
| 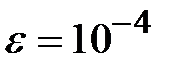
| |
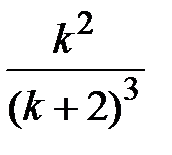
| 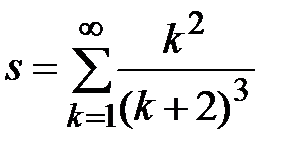
| 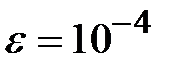
| |
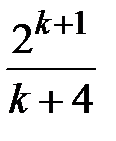
| 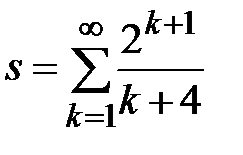
| 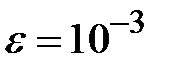
| |
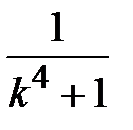
| 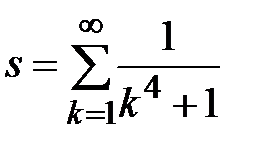
| 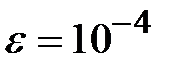
| |
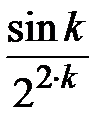
| 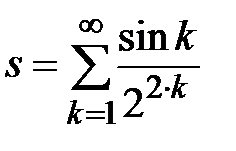
| 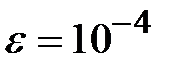
| |
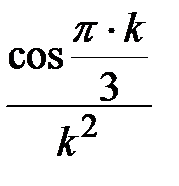
| 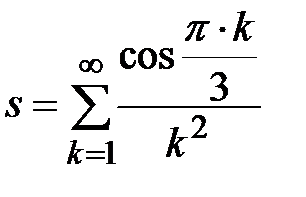
| 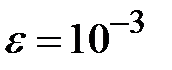
| |
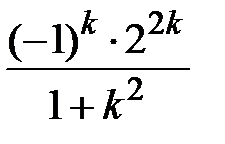
| 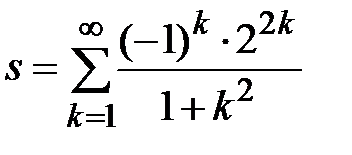
| 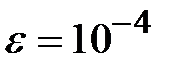
|
Задание № 4. Вычислить наименьшее значение функции 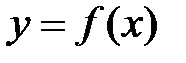 и наибольшее значение функции
и наибольшее значение функции 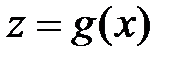 на отрезке
на отрезке 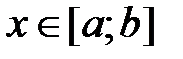 c шагом
c шагом 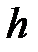 . Где
. Где 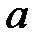 ,
, 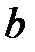 ,
, 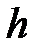 – вещественные числа,
– вещественные числа, 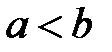 ,
,  .
.
| № | Функция 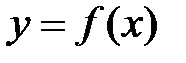
| Функция 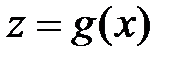
|
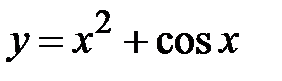
| 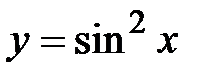
| |
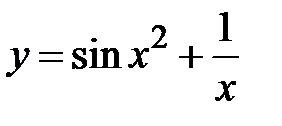
| 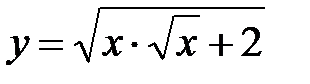
| |
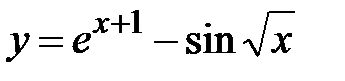
| 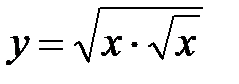
| |
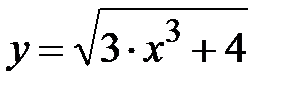
| 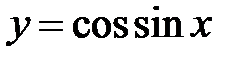
| |
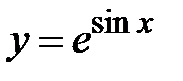
| 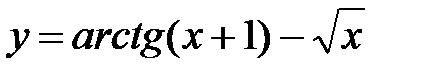
| |
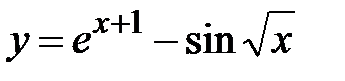
| 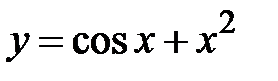
| |
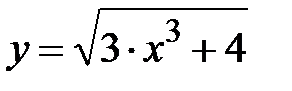
| 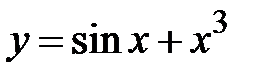
| |
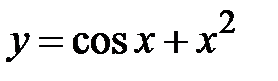
| 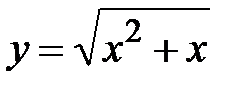
| |
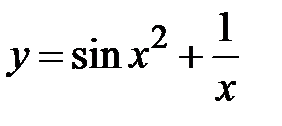
| 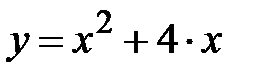
| |
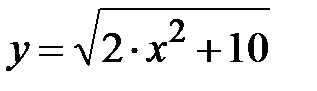
| 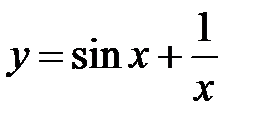
| |
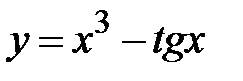
| 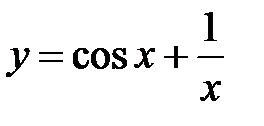
| |
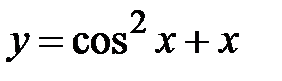
| 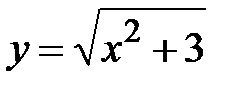
| |
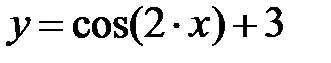
| 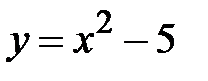
| |
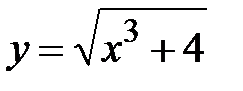
| 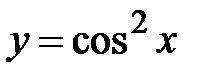
| |
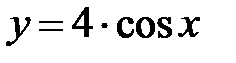
| 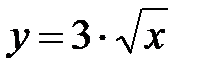
| |
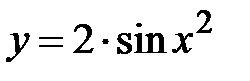
| 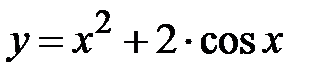
| |
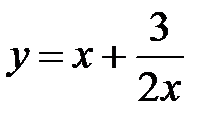
| 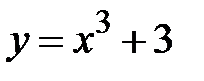
| |
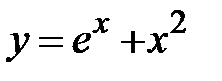
| 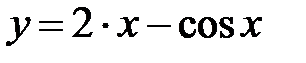
| |
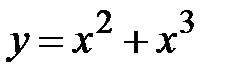
| 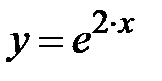
| |
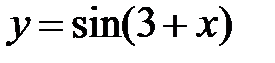
| 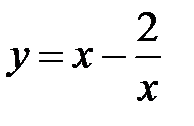
| |
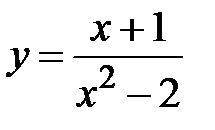
| 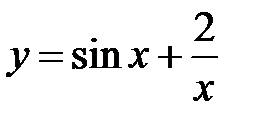
| |
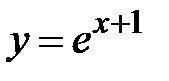
| 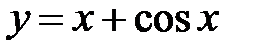
| |
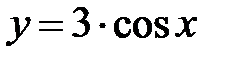
| 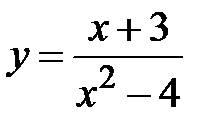
| |
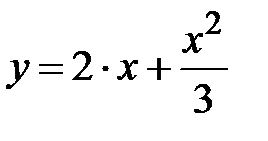
| 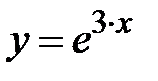 + x + x
| |
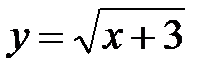
| 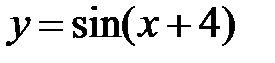
| |
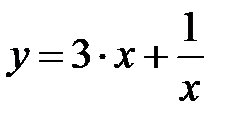
| 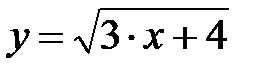
| |
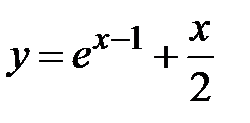
| 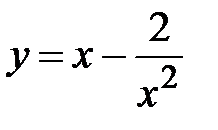
| |
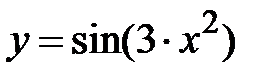
| 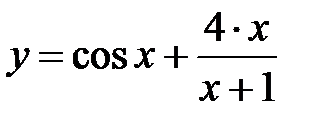
| |
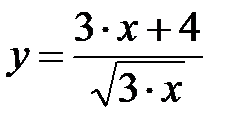
| 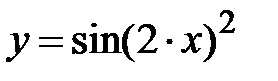
| |
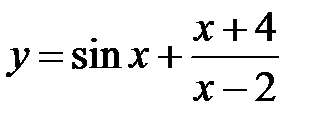
| 
|
Задание № 5. Составить программу на языке программирования Паскаль для нахождения минимального и максимального значений функции на заданном отрезке.
Вариант №1
1) Найти максимум функции f(x)= 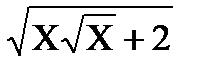 ; x Є [4; 5], h=0. 2.
; x Є [4; 5], h=0. 2.
2) Найти минимум функции f(x) = sinx2 + 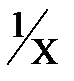 ; x Є [1; 4], h=0. 2.
; x Є [1; 4], h=0. 2.
Вариант №2
1) Найти максимум функции f(x)= 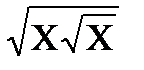 ; x Є [0; 4], h=0. 2.
; x Є [0; 4], h=0. 2.
2) Найти минимум функции f(x) = ex+1 - sin 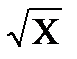 ; x Є [3; 7], h=0. 5.
; x Є [3; 7], h=0. 5.
Вариант №3
1) Найти максимум функции f(x)= 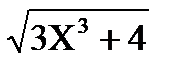 ; x Є [2; 3], h=0. 1.
; x Є [2; 3], h=0. 1.
2) Найти минимум функции f(x) = cossinx; x Є [0; 3], h=0. 3.
Вариант №4
1) Найти максимум функции f(x)=arctg(x+1) - 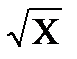 ; где x Є [0; 1], h=0. 1.
; где x Є [0; 1], h=0. 1.
2) Найти минимум функции f(x) = esinx; где x Є [-1; 3], h=0. 1.
Вариант №5
1) Найти максимум функции f(x)=cosx +x2; где x Є [0; 2], h=0. 2.
2) Найти минимум функции f(x) = ex+1 - sin 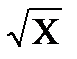 ; где x Є [3; 7], h=0. 5.
; где x Є [3; 7], h=0. 5.
Вариант №6
1) Найти максимум функции f(x)=sinx +x3; где x Є [0; 1], h=0. 3.
2) Найти минимум функции f(x) = 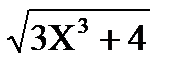 ; где x Є [2; 3], h=0. 1.
; где x Є [2; 3], h=0. 1.
Вариант №7
1) Найти максимум функции f(x)= 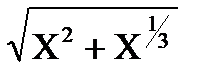 ; где x Є [0; 5], h=1.
; где x Є [0; 5], h=1.
2) Найти минимум функции f(x) = cosx + x2; где x Є [0; 2], h=0. 2.
Вариант №8
1) Найти максимум функции f(x)=x2 + 4x; где x Є [1; 3], h=0. 2.
2) Найти минимум функции f(x) = sinx2 + 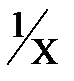 ; где x Є [1; 4], h=0. 3.
; где x Є [1; 4], h=0. 3.
Вариант №9
1) Найти максимум функции f(x)= sinx + 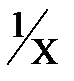 ; где x Є [2; 5], h=0. 1.
; где x Є [2; 5], h=0. 1.
2) Найти минимум функции f(x) = 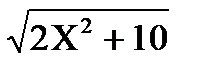 ; где x Є [-5; 5], h=1.
; где x Є [-5; 5], h=1.
Вариант №10
1) Найти максимум функции f(x)=sinx + 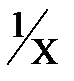 ; где x Є [2; 5], h=0. 5.
; где x Є [2; 5], h=0. 5.
2) Найти минимум функции f(x) = x3 - tgx; где x Є [2; 5], h=0. 1.
Вариант №11
1) Найти максимум функции f(x)= 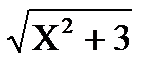 ; где x Є [-1; 1], h=0. 1.
; где x Є [-1; 1], h=0. 1.
2) Найти минимум функции f(x) = cos2x + x; где x Є [0; 2], h=0. 2.
Задание № 6. Составить таблицу значений функции  , для аргумента, изменяющегося на отрезке
, для аргумента, изменяющегося на отрезке 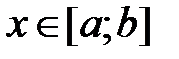 с постоянным шагом
с постоянным шагом 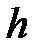 .
.
| № | Функция 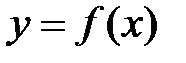
| Отрезок 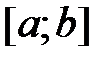
| Шаг, 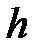
|
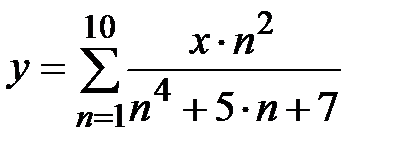
| 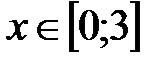
| 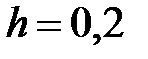
| |
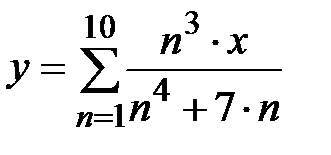
| 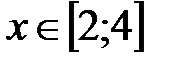
| 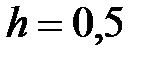
| |
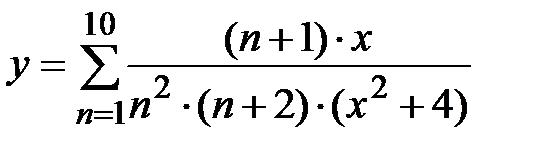
| 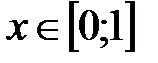
| 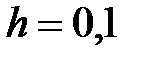
| |
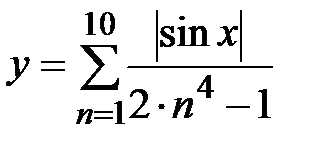
| 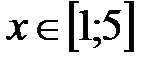
| 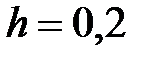
| |
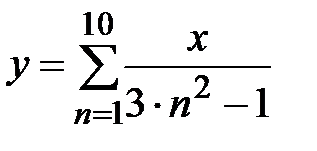
| 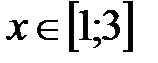
| 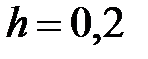
| |
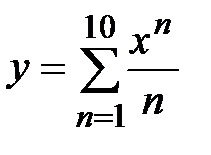
| 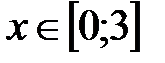
| 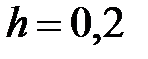
| |
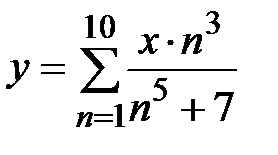
| 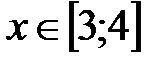
| 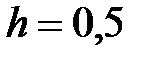
| |
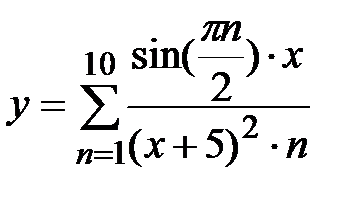
| 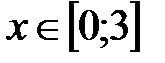
| 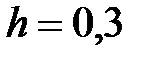
| |

| 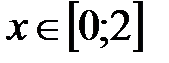
| 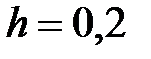
| |
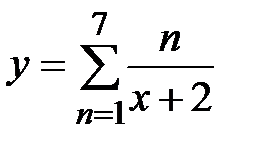
| 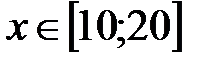
| 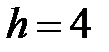
| |
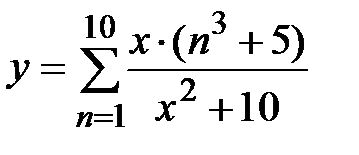
| 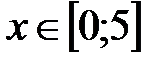
| 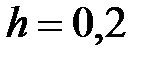
| |
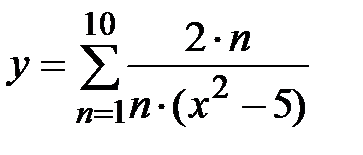
| 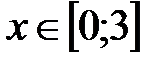
| 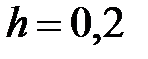
| |
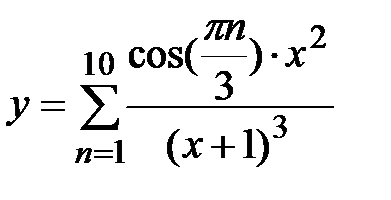
| 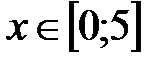
| 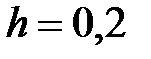
| |
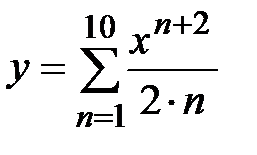
| 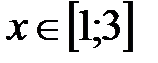
| 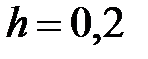
| |
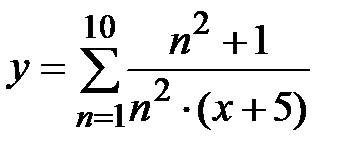
| 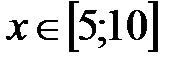
| 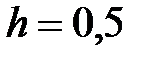
| |
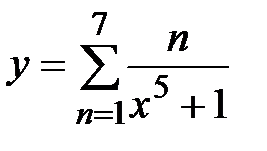
| 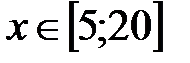
| 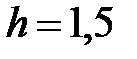
| |

| 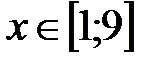
| 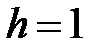
| |
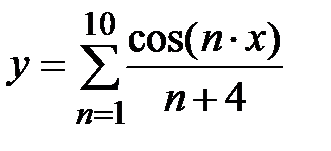
| 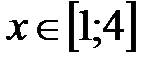
| 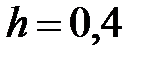
| |
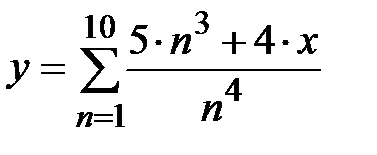
| 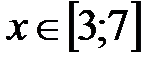
| 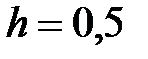
| |
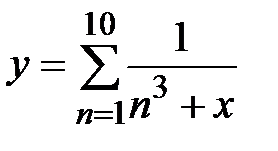
| 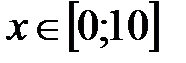
| 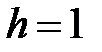
| |
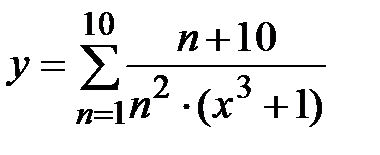
| 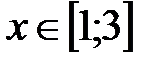
| 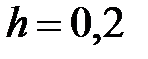
| |
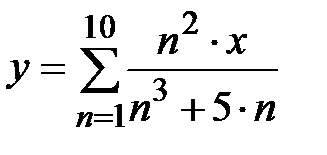
| 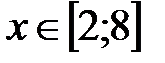
| 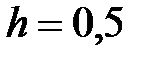
| |
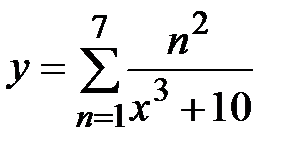
| 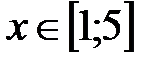
| 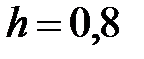
| |
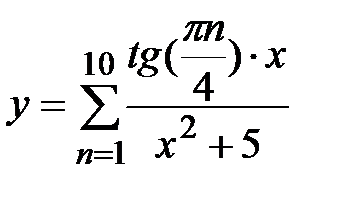
| 
| 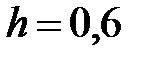
| |
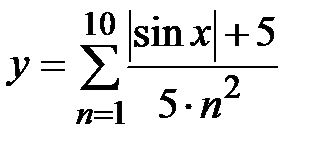
| 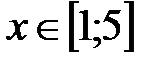
| 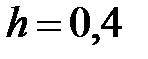
| |
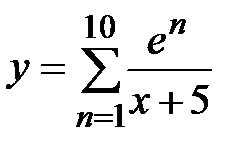
| 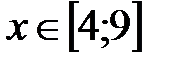
| 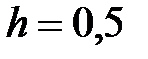
| |
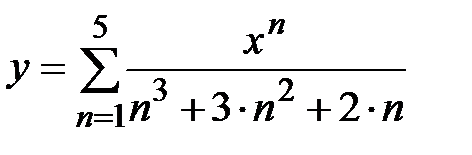
| 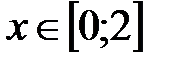
| 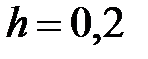
| |
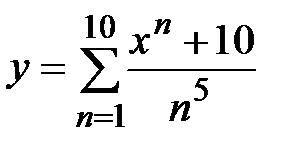
| 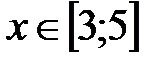
| 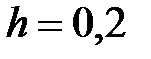
| |
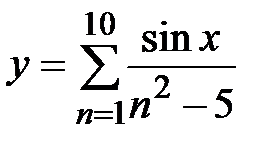
| 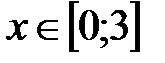
| 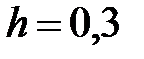
| |
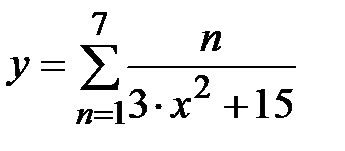
| 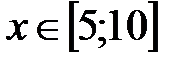
| 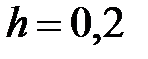
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|