Контакты

Случайная статья

Решение иррациональных уравнений и неравенств методом введения новой переменной.

Решение иррациональных уравнений и неравенств методом введения новой переменной.

При изучении темы « решение иррациональных уравнений и неравенств» целесообразно вводить способ введения новой переменной, который облегчает решения некоторых уравнений и неравенств.

Например: Уравнения и неравенства вида 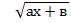= сх+d, 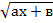> сх+d, 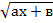< сх+d проще решать заменой переменной.

1. = х - 6

Пусть 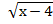=t, где t≥ 0, тогда х-4= 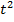, х=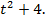

Данное уравнение примет вид: t = 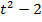, 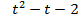=0, t=2; t=-1 ( не удовлетворяет условию t≥ 0), значит х=4+4; х=8

Ответ: 8

2. х-1

Пусть =t, где t≥ 0, тогда 3х-5= 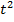; х = ;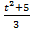

Данное неравенство примет вид: t< 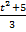; 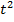-3t+2> 0; 0≤ t< 1 или t> 2.

0≤ < 1 или > 2

0≤ 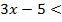1 3х-5 > 4

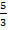≤ x< 2 х> 3

Ответ: [ ; 2); (3; ∞ )

3. + =7

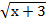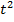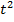Пусть = t, где t≥ 0, тогда х+3= , х= -3.

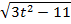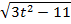Данное уравнение примет вид: t + =7; = 7-t

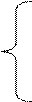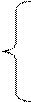0 ≤ t ≤ 7 0 ≤ t ≤ 7

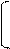; t=-10

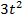-11=49-14t+ 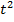, t=3

t=3, значит х=6

Ответ: 6.

4. 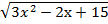+ 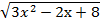=7

Пусть 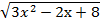=t, , где t≥ 0, тогда 3 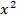-2х +8= 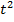, данное уравнение примет вид: 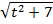+t=7, решая получившиеся иррациональное уравнение, находим значения х.

Для некоторых иррациональных уравнений целесообразно вводить две переменные.

Например: −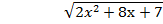

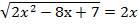
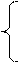Пусть 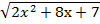= t, t≥ 0 =v, v≥ 0, тогда = ,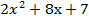

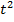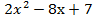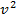= . Составим систему: 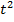− 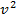=16х

t− v= 2x

Решая данную систему, находим значение x=0 или t=x+4.

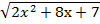= x+4, решая данное уравнение, находим его корни, х=3, х=-3

Ответ: -3; 3; 0.

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.