((x≤9) → (x·x<A))/\ ((y·y<A) → (y<12)) = 1

Задание 15 часть 1

Для какого наименьшего целого числа А формула

((x≤ 9) → (x·x< A))/\ ((y·y< A) → (y< 12))

тождественно истинна (то есть принимает значение 1 при любых целых неотрицательных значениях переменных x и y)?

Решение

((x≤ 9) → (x·x< A))/\ ((y·y< A) → (y< 12)) = 1

x≤ 9 -> x = 9

x·x< A

9*9 < A

81 < A = 82

Ответ: 82.

Еще пример подобного задания

Для какого наибольшего целого числа А формула

((x ≤ 9) → (x⋅ x ≤ A)) ⋀ ((y⋅ y ≤ A) → (y ≤ 9))

тождественно истинна, то есть принимает значение 1 при любых целых неотрицательных x и y?

Решение:

В формуле имеется операция ^ - конъюнкция (логическое умножение), при нём в результате получится истинна если только все выражения будут истинными.

((x ≤ 9) → (x⋅ x ≤ A)) = 1

((y⋅ y ≤ A) → (y ≤ 9)) = 1

Рассмотрим скобки раздельно, избавимся от → - импликации (логическое следование).

A→ B = AvB => (x > 9) v (x² ≤ A) между скобками получилась операция дизъюнкция (логическая сумма), при данной операции истинна будет, если хотя бы одно из выражений истинно.

При x> 9 [ (x > 9) v (x² ≤ A) ] – уже будет истинным, но при x[0; 9] (диапазон от 0 потому что в условии сказано: при любых целых неотрицательных x и y) выражение в первой скобки станет ложным и возникает необходимость проверки выражения во второй (x² ≤ A). В этой ситуации от ложного результата и должна спасти переменная А.

Значит чтобы (x² ≤ A)=1 => А> = x² (x ≤ 9) => A> =81.

Аналогично рассмотрим вторую часть выражения ((y⋅ y ≤ A) → (y ≤ 9)) = 1

(y2> =A) v (y ≤ 9)=1

y [10; +∞ ) => y2 > A => A< 100

т. е. 81 ≤ A < 100

По условию задачи надо найти максимальное А => A = 99

Ответ: 99

И еще пример

Для какого наибольшего целого неотрицательного числа А выражение

(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y)

тождественно истинно, т. е. принимает значение 1 при любых целых неотрицательных x и y?

Решение:

Разделим общее выражение на две части. Выделим неизвестную часть красным:

(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y)

Неизвестная часть должна быть истинной, она обязательно будет истинна, если известная часть — ложь:

(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y) = 1

⁰ ¹

Т. е. 48 ≠ y + 2x = 0 или y + 2x = 48. На графике это уравнение представляет линию. Из условия имеем два ограничения: (x > 0) and (y > 0). Отобразим линию для 1-й четверти, соответствующей положительным x и y:

y + 2x = 48:

при x = 0, y = 48

при y = 0, 2x = 48 => x = 24

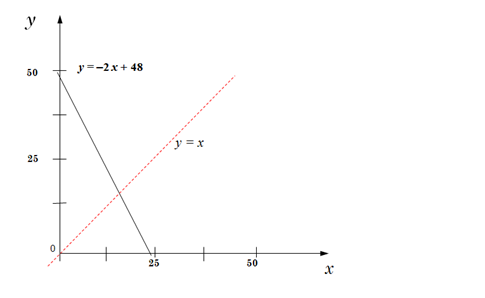
Возьмем некоторое значение A, например, A = 25, отметим его на графике белой областью так, чтобы выполнялось (A < x) ∨ (A < y). По условию имеем, что все точки данной части отрезка прямой y + 2x = 48 должны принадлежать отмеченной белой области. Заштрихуем область для всех точек прямой (голубым цветом):

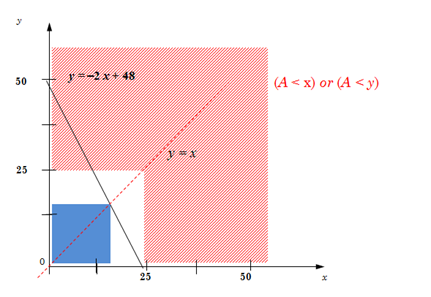
То есть все точки голубого квадрата должны находиться под отрезком линии (включая вершину (A, A) ), и данный квадрат, соответствует максимальному значению A.

Наибольшее значение голубая область приобретает в точке пересечения прямой y + 2x = 48 с прямой y = x:

Далее решаем полученное линейное уравнение (для x = y ):

x + 2x = 48 =>

3x = 48

x = 16

Так как значение A должно быть меньше x, то наибольшее А = 15.

Результат: 15