
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Система оценивания экзаменационной работы по математике
Система оценивания экзаменационной работы по математике
(профильный уровень)
Каждое из заданий 1–12 считается выполненными верно, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби. Каждое верно выполненное задание оценивается 1 баллом.
| Номер задания | Правильный ответ |
| 0, 25 | |
| -0, 5 | |
| -12 | |
| -1 |
Решения и критерии оценивания выполнения заданий с развёрнутым
ответом
Количество баллов, выставленных за выполнение заданий 13–19, зависит
от полноты решения и правильности ответа.
Общие требования к выполнению заданий с развёрнутым ответом: решение должно быть математически грамотным, полным; все возможные случаи должны быть рассмотрены. Методы решения, формы его записи и формы записи ответа могут быть разными. За решение, в котором обоснованно получен правильный ответ, выставляется максимальное количество баллов. Правильный ответ при отсутствии текста решения оценивается в 0 баллов.
Эксперты проверяют только математическое содержание представленного решения, а особенности записи не учитывают.
При выполнении задания могут использоваться без доказательства и ссылок любые математические факты, содержащиеся в учебниках и учебных пособиях, входящих в Федеральный перечень учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ среднего общего образования.
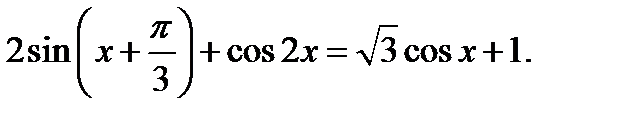
б) Укажите корни этого уравнения, принадлежащие отрезку 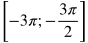
Решение. а) Запишем исходное уравнение в виде:
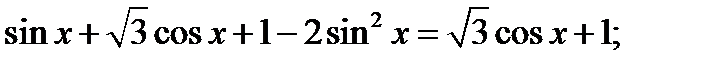
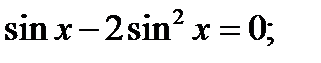
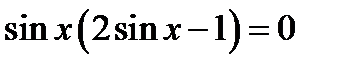 .
. 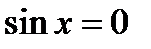 или
или 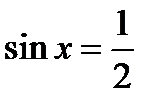 ;
; 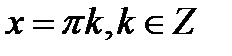 или
или 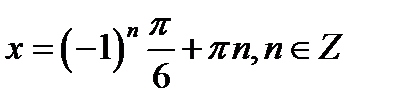 .
.
б) С помощью числовой окружности отберем корни уравнения, принадлежащие отрезку [-3π; 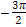 ]. Получим числа:
]. Получим числа: 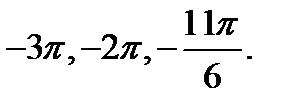
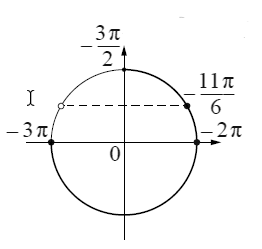
Ответ: 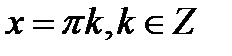 или
или 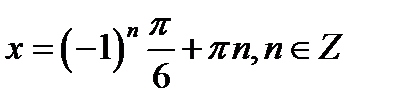 ;
; 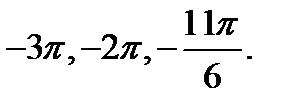
| Содержание критерия | Баллы |
| Обоснованно получены верные ответы в обоих пунктах | |
| Обоснованно получен верный ответ в пункте а, ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения обоих пунктов: пункта а и пункта б | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
а) Докажите, что прямые BM и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и ABB1.
Решение. а) Пусть точка H — середина AC. Тогда 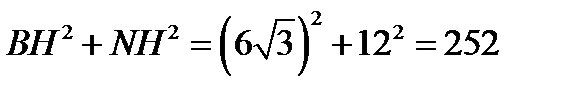
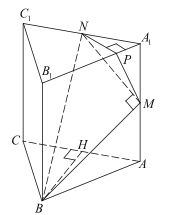 Вместе с тем
Вместе с тем 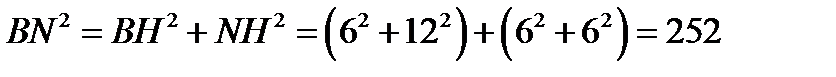 ,
,
тогда по теореме, обратной теореме Пифагора, треугольник BMN является прямоугольным с прямым углом M.
б) Проведём перпендикуляр NP к прямой A1B1, кроме нее NP⊥ A1A. Следовательно, NP ⊥ ABB1. Поэтому MP — проекция MN на плоскость ABB1.
Прямая BM перпендикулярна MN, тогда по теореме о трёх перпендикулярах BM⊥ MP. Следовательно, угол NMP — линейный угол искомого угла.
Длина NP равна половине высоты треугольника A1B1C1, т. е. NP = 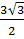 .
.
Поэтому 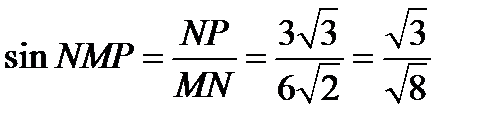 . Следовательно,
. Следовательно, 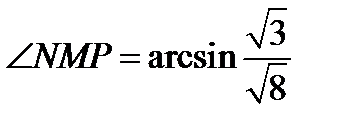 . Ответ: б)
. Ответ: б) 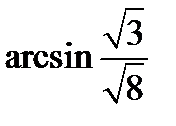
| Содержание критерия | Баллы |
| Имеется верное доказательство пункта а и обоснованно получен верный ответ в пункте б. | |
| Имеется верное доказательство пункта а ИЛИ обоснованно получен верный ответ в пункте б, возможно с использованием утверждения пункта а, при этом пункт а не выполнен | |
| Решение не соответствует ни одному из критериев, приведенных выше | |
| Максимальный балл |
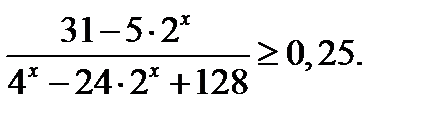
Решение. Обозначим 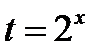 . тогда неравенство принимает вид
. тогда неравенство принимает вид 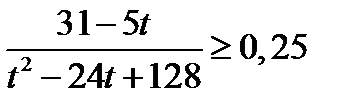 .
.
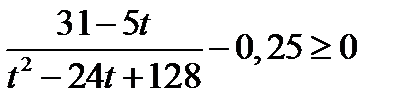
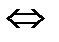
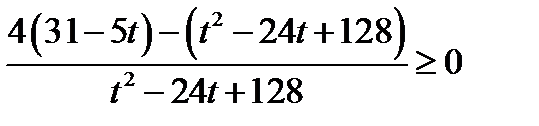
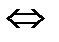
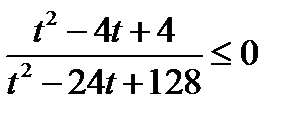
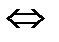
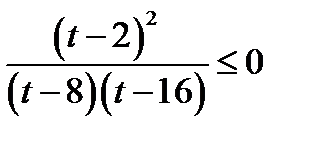
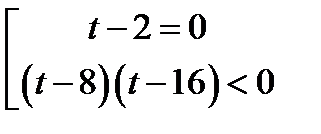
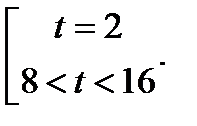
Возвращаясь к исходной переменной, имеем:
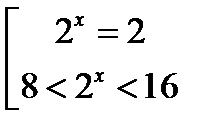
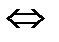
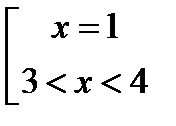 ,
, 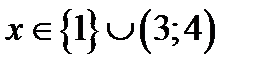
Ответ: 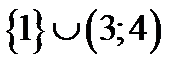
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
| Обоснованно получен ответ, отличающийся от верного исключением точки 1 ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
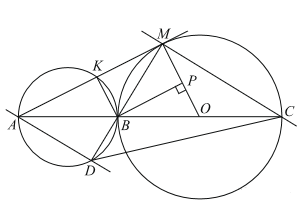
а) Докажите, что прямые AD и MC параллельны.
б) Найдите площадь треугольника DBC, если AK = 4 и MK = 12.
Решение.
а) Точки M и D лежат на окружностях с диаметрами BC и AB соответственно, поэтому 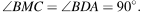
Прямые AD и MC перпендикулярны одной и той же прямой MD, следовательно, прямые AD и MC параллельны.
б) Пусть O — центр окружности с диаметром BC. Тогда прямые OM и AM перпендикулярны.
Учитывая, что прямые BK и AM перпендикулярны, получаем, что прямые OM и BK параллельны. Обозначим BK через x. Треугольник AMO подобен треугольнику AKB с коэффициентом 4, поэтому OB = OM = 4x. Опустим перпендикуляр BP из точки B на прямую OM. Так как четырёхугольник BKMP — прямоугольник,
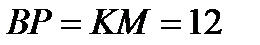 .
.
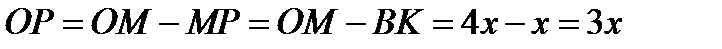 .
.
По теореме Пифагора OB2 = BP2 + OP2, откуда 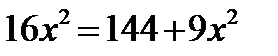 . Получаем, что
. Получаем, что 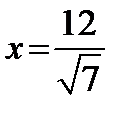 .
.
Поскольку прямые AD и MC параллельны, 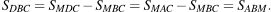
Значит, треугольники DBC и AMB равновелики. Следовательно, 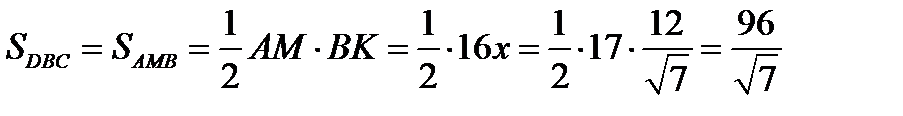
Ответ: 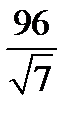 .
.
| Содержание критерия | Баллы |
| Имеется верное доказательство утверждения пункта а, и обоснованно получен верный ответ в пункте б | |
| Обоснованно получен верный ответ в пункте б, ИЛИ имеется верное доказательство утверждения пункта а, и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а, ИЛИ при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки, ИЛИ Обоснованно получен верный ответ в пункте б с использованием утверждения пункта а, при этом пункт а не выполнен | |
| Решение не соответствует ни одному из критериев, приведенных выше | |
| Максимальный балл |
— в январе каждого года долг увеличивается на 30% по сравнению с предыдущим годом;
— с февраля по июнь нужно выплатить часть долга одним платежом.
Определите, на какую сумму взяли кредит банке, если известно, что кредит был выплачен тремя равными платежами (за 3 года) и общая сумма выплат на 156 060 рублей больше суммы взятого кредита.
Решение.
Пусть в кредит планируется взять S рублей, а ежегодный платеж по кредиту будет составлять x рублей. Тогда каждый год долг увеличивается на 30% или в 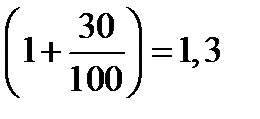 раза и уменьшается на x рублей.
раза и уменьшается на x рублей.
Тогда в первый год долг составит: 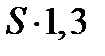 остаток будет равен
остаток будет равен 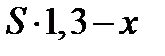 .
.
После второго года остаток по кредиту составит: 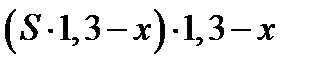 .
.
В конце третьего года он будет равен 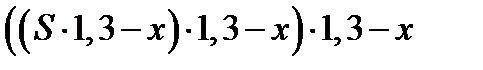 .
.
По условию кредит был погашен за 3 года, а это значит, что остаток за третий год равен 0, то есть:
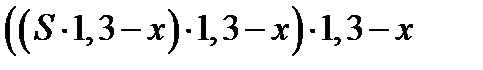 =0,
=0, 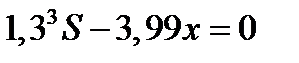 ,
, 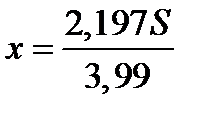
По условию общая сумма выплат на 156 060 рублей больше суммы взятого кредита, а значит:
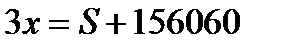 ,
, 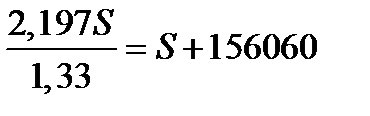 ,
, 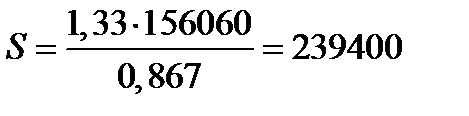
Ответ: 239 400 рублей.
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
| Верно построена математическая модель, решение сведено к исследованию этой модели и получен результат: -неверный ответ из-за вычислительной ошибки; - верный ответ, но решение недостаточно обосновано | |
| Верно построена математическая модель, решение сведено к исследованию этой модели, при этом решение может быть не завершено | |
| Решение не соответствует ни одному из критериев, приведенных выше | |
| Максимальный балл |
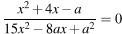
имеет ровно два различных решения.
Решение.
Заметим, что
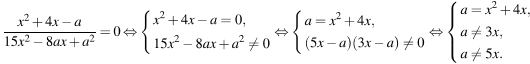
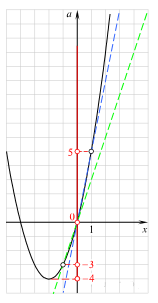 Изобразим решение в системе координат xOa. Графиком системы, а значит, и графиком исходного уравнения является парабола с выколотыми точками. Ординаты точек пересечения параболы
Изобразим решение в системе координат xOa. Графиком системы, а значит, и графиком исходного уравнения является парабола с выколотыми точками. Ординаты точек пересечения параболы 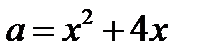 и прямой
и прямой 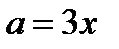 найдём из уравнения
найдём из уравнения 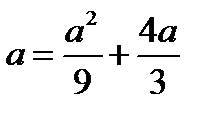 .
.
Получаем a=0 или a=-3.
Ординаты точек пересечения параболы 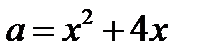 и прямой
и прямой 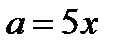 найдём из уравнения
найдём из уравнения 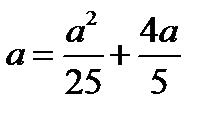 . Получаем a=0 или a=5
. Получаем a=0 или a=5
Ровно два решения исходное уравнение имеет при 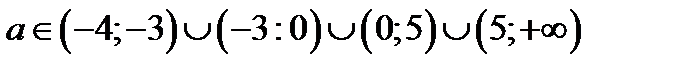
Ответ: 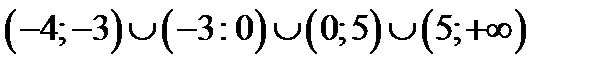
| Содержание критерия | Баллы |
| Обоснованно получен верный ответ | |
| С помощью верного рассуждения получены все значения a, но ответ содержит лишнее значение, или решение недостаточно обосновано | |
| С помощью верного рассуждения получено хотя бы одно верное значение параметра | |
| Задача верно сведена к исследованию возможного значения корней уравнения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
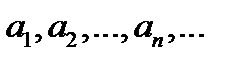 и
и 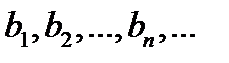 являются натуральными числами.
являются натуральными числами.
а) Приведите пример таких прогрессий, для которых 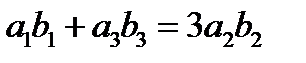 .
.
б) Существуют ли такие прогрессии, для которых 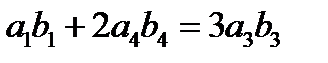 ?
?
в) Какое наибольшее значение может принимать произведение 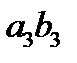 , если
, если 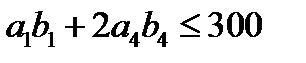 ?
?
Решение.
а) Подходящим примером являются прогрессии 1, 3, 5,... и 1, 4, 7,... Для этих прогрессий имеем 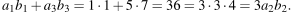
б) Обозначим через c и d разности арифметических прогрессий 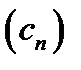 и
и 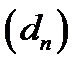 соответственно.
соответственно.
Тогда 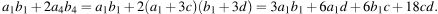
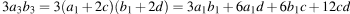 и
и 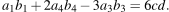
Если 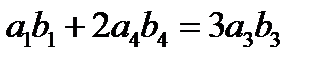 то
то 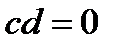
Получаем противоречие, ведь по условию 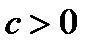 и
и 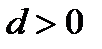 .
.
в) По условию 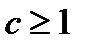 и
и 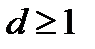 В ходе решения пункта б мы получили, что
В ходе решения пункта б мы получили, что 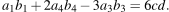
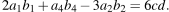 Значит,
Значит,
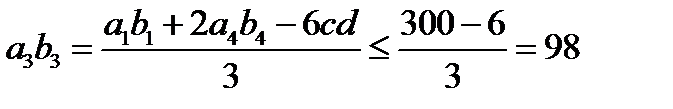 , то есть
, то есть 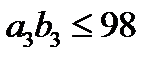 .
.
Покажем, что случай 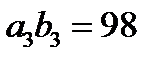 возможен. Это равенство выполняется, например, для прогрессий 5, 6, 7, 8,... и 12, 13, 14, 15,... Для них
возможен. Это равенство выполняется, например, для прогрессий 5, 6, 7, 8,... и 12, 13, 14, 15,... Для них 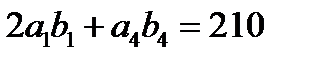 и
и 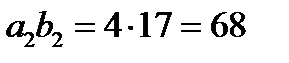 .
.
Ответ: а) 1, 3, 5,... и 1, 4, 7,...; б) нет; в) 98.
| Содержание критерия | Баллы |
| Верно получены все перечисленные (см. критерий на 1 балл) результаты | |
| Верно получены три из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получены два из перечисленных (см. критерий на 1 балл) результатов | |
| Верно получен один из следующих результатов: – обоснованное решение пункта а; – обоснованное решение пункта б; – искомая оценка в пункте в; – пример в пункте в, обеспечивающий точность предыдущей оценки | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|