Контакты

Случайная статья

Практическая работа № 12

Тема: Расчет неразветвленной линейной электрической цепи с активным и реактивным сопротивлениями при несинусоидальном напряжении.

Цель: Выработать практические навыки для расчёта мгновенных и действующих значений токов, определения активной мощности.

Пример:

Катушка с активным сопротивлением и индуктивностью соединена последовательно с конденсатором. На зажимах цепи действует несинусоидальное напряжение.

Дано: u= 250+340sinwt+180sin3wt+89sin5wt L= 15, 9 мГн R= 25 Ом С= 63 мкФ f=50 Гц Определить; I, i, P-?

Решение:

1. Сопротивление цепи для постоянной составляющей тока равно бесконечности, так как в цепи имеется конденсатор. Постоянная составляющая тока равна нулю:

I₀=0

Сопротивление цепи для первой гармоники

R=25 Ом; X₁_L=w1× L=314× 15, 9× 10^-3=5 Ом;

X₁_c= 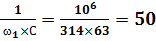Ом;

Z₁= 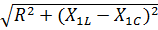= 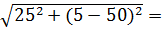51, 48 Ом.

Реактивное сопротивление току первой гармоники имеет ёмкостный характер:

Cos j1= 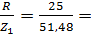0, 49; j1=arcos 0, 49=61

Амплитуда тока первой гармоники

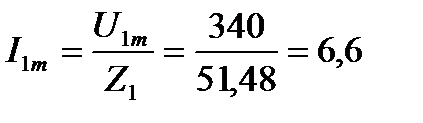A

2. Сопротивление цепи для третьей гармоники:

Z₃= =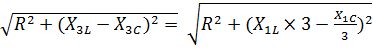

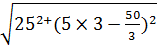
=25, 06 Ом.

Реактивное сопротивление току третьей гармоники имеет ёмкостный характер:

Cos j3= 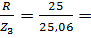0, 997; j3=arcos 0, 997=4

Амплитуда тока третьей гармоники

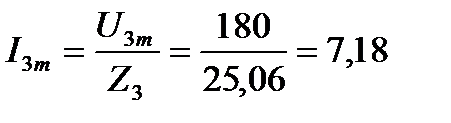A

3. Сопротивление цепи для пятой гармоники:

Z₅= =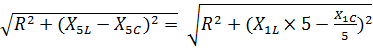

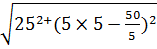
=29, 15 Ом.

Реактивное сопротивление току пятой гармоники имеет индуктивный характер:

Cos j5= 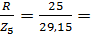0, 86; j5=arcos 0, 86=31

Амплитуда тока пятой гармоники

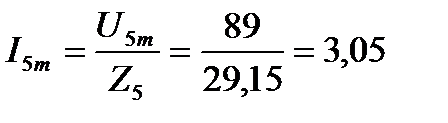A

4. Действующие значения токов первой, третьей и пятой гармоник

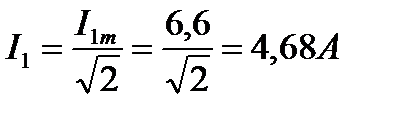
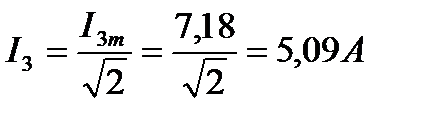
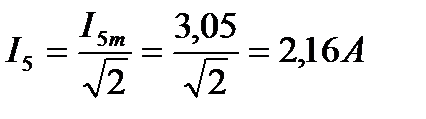
5. Действующее значение тока в цепи:

I= 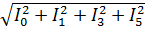= =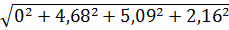7, 24 A

6. Уравнение мгновенного значения тока

i= 6, 6sin(wt+61 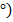+7, 18sin(3wt+4 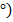+3, 05sin(5wt-31 ) A

7. Активная мощность в цепи:

Р=Р₀+Р₁+Р₃+Р₅

Р₀=U₀× I₀=250× 0=0

P₁=U₁× I₁× cos j₁= 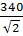× × 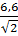0, 49=553 Вт

P₃=U₃× I₃× cos j₃= 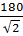× × 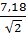0, 997=651. 67 Вт

P₅=U₅× I₅× cos j₅= 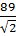× × 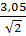0, 86=117, 25 Вт

Р=553+ 651, 67 + 117, 25=1321, 9 В

Таблица:

Вар-т Данные
F, Гц
L, мГн
С, мкФ
R, Ом
U0, B
U1, B
U3, B
U5, B

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.