Независимые события Умножения вероятностей Сложение вероятностей Статистическая вероятность

04. 04. 22 г.

Алгебра

Независимые события Умножения вероятностей Сложение вероятностей Статистическая вероятность

ГИА 2022

1. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0, 3. Вероятность того, что кофе закончится в обоих автоматах, равна 0, 12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Решение.

Рассмотрим события

А - событие кофе закончится в первом автомате,

В – событие кофе закончится во втором автомате.

Тогда

A·B = кофе закончится в обоих автоматах,

A  +  B = кофе закончится хотя бы в одном автомате.

По условию P(A)  =  P(B)  =  0, 3; P(A·B)  =  0, 12.

События A и B совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:

P(A  +  B)  =  P(A)  +  P(B)  −   P(A·B)  =  0, 3  +  0, 3  −   0, 12  =  0, 48.

Следовательно, вероятность противоположного события, состоящего в том, что кофе останется в обоих автоматах, равна 1  −   0, 48  =  0, 52.

Ответ: 0, 52.

№ 3. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0, 52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0, 3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Решение.

Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0, 52  ·  0, 3  =  0, 156.

Ответ: 0, 156.

№ 4. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 70% этих стекол, вторая – 30%. Первая фабрика выпускает 5% бракованных стекол, а вторая – 4%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным (Решить дома).

Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 60% этих стекол, вторая  — 40%. Среди стёкол, выпускаемых первой фабрикой, брак составляет 3%. Среди стёкол, выпускаемых второй фабрикой, брак составляет 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Спрятать решение

Решение.

Вероятность того, что стекло сделано на первой фабрике и оно бракованное: 0, 6  ·  0, 03  =  0, 018.

Вероятность того, что стекло сделано на второй фабрике и оно бракованное: 0, 4  ·  0, 01  =  0, 004.

Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным равна 0, 018  +  0, 004  =  0, 022.

Ответ: 0, 022.

№ 5. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Сапфир» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Сапфир» выиграет жребий ровно два раза.

Решение.

Обозначим «1» ту сторону монеты, которая отвечает за выигрыш жребия «Сапфир», другую сторону монеты обозначим  «0». Тогда благоприятных комбинаций три: 110, 101, 011, а всего комбинаций 2³  =  8: 000, 001, 010, 011, 100, 101, 110, 111. Тем самым, искомая вероятность равна: Р=3: 8=0, 375

Ответ: 0, 375.

Задание 6. Найдите вероятность того, что случайно выбранное трёхзначное число делится на 49.

Решение.

Трехзначные числа, делящиеся на 49 можно найти путем умножения этого числа на 3, 4, 5, …, 20. То есть, имеем m=18 трехзначных чисел, делящихся на 49. Всего же трехзначных чисел от 100 до 999, что равно n=900 вариантам.

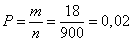
Ответ: 0, 02.

№ 7. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.

Решение.

Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6  =  36. Следовательно, вероятность того, что в сумме выпадет 8  очков, равна: Р=5: 36=0, 14

Ответ: 0, 14.

№ 8. Ковбой Джон попадает в муху на стене с вероятностью 0, 9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0, 2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся (дома)

Ковбой Джон попадает в муху на стене с вероятностью 0, 8, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0, 2. На столе лежит 10 револьверов, из них только 2 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

Решение.

Джон промахнется, если схватит пристрелянный револьвер и промахнется из него, или если схватит непристрелянный револьвер и промахнется из него. По формуле условной вероятности, вероятности этих событий равны соответственно 0, 2·(1  −   0, 8)  =  0, 04 и 0, 8·(1  −   0, 2)  =  0, 64. События схватить пристрелянный или непристрелянный револьвер образуют полную группу (они несовместны и одно из них непременно наступает), поэтому, по формуле полной вероятности, Джон промахнется с вероятностью 0, 04  +  0, 64  =  0, 68.

Ответ: 0, 68.

Домашнее задание Читать П 68 стр. 346-348 Решить №1134, №1135 №1136(2, 3)№1137