Система основных понятий

Класс: 10 класс

Пятнадцатое февраля

Урок по теме: «Модели оптимального планирования.

Стратегическая цель планирования. Задача линейного программирования»

Объектами планирования могут быть самые разные системы: деятельность отдельного предприятия, отрасли промышленности или сельского хозяйства, региона, наконец государства.

Постановка задачи планирования выглядит следующим образом:

· имеются некоторые плановые показатели: X, У, и др.;

· имеются некоторые ресурсы: R1, R2 и др., за счет которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены;

· имеется определенная стратегическая цель, зависящая от значений X, У и др. плановых показателей, на которую следует ориентировать планирование.

Нужно определить значение плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели. Это и будет оптимальным планом.

Приведём примеры. Пусть объектом планирования является детский сад. Ограничимся лишь двумя плановыми показателями: количеством детей и количеством воспитателей. Основными ресурсами деятельности детского сада являются объем финансирования и площади помещения. А каковы стратегические цели? Естественно, одной из них является сохранение и укрепление здоровья детей. Количественной мерой такой цели является минимизация заболеваемости воспитанников детского сада.

Другой пример: планирование экономической деятельности государства. Безусловно, это слишком сложная задача для того, чтобы нам с ней полностью разобраться. Плановых показателей очень много: это производство различных видов промышленной и сельскохозяйственной продукции, подготовка специалистов, выработка электроэнергии, размер зарплаты работников бюджетной сферы и многое другое. К ресурсам относятся: количество работоспособного населения, бюджет государства, природные ресурсы, энергетика, возможности транспортных систем и пр.

Как вы понимаете, каждый из этих видов ресурсов ограничен. Кроме того, важнейшим ресурсом является время, отведенное на выполнение плана. Вопрос о стратегических целях довольно сложный. У государства их много, но в разные периоды истории приоритеты целей могут меняться. Например, в военное время главной целью является максимальная обороноспособность, военная мощь страны. В мирное время в современном цивилизованном государстве приоритетной целью должно быть достижение максимального уровня жизни населения.

Если мы хотим использовать компьютер для решения задачи оптимального планирования, то нам снова нужно построить математическую модель. Следовательно, все, о чем говорилось в примерах, должно быть переведено на язык чисел, формул, уравнений и других средств математики. В полном объеме для реальных систем эта задача очень сложная. Как и раньше, мы пойдем по пути упрощения. Рассмотрим очень простой пример, из которого вы получите представление об одном из подходов к решению задачи оптимального планирования.

Пример. Школьный кондитерский цех готовит пирожки и пирожные. В силу ограниченности емкости склада за день можно приготовить в совокупности не более 700 штук изделий. Рабочий день в кондитерском цехе длится 8 часов. Поскольку производство пирожных более трудоемко, то если выпускать только их, за день можно произвести не более 250 штук, пирожков же можно произвести 1000 штук (если при этом не выпускать пирожных). Стоимость пирожного вдвое выше, чем стоимость пирожка. Требуется составить такой дневной план производства, чтобы обеспечить наибольшую выручку кондитерского цеха.

Разумеется, это чисто учебный пример. Вряд ли существует такой кондитерский цех, который выпускает всего два вида продукции, да и наибольшая выручка — не единственная цель его работы. Но зато математически формулировка задачи будет простой. Давайте ее выработаем.

Плановыми показателями являются:

· х — дневной план выпуска пирожков;

· у — дневной план выпуска пирожных.

Что в этом примере можно назвать ресурсами производства? Из того, о чем говорится в условии задачи, это:

· длительность рабочего дня — 8 часов;

· вместимость складского помещения — 700 мест.

Предполагается для простоты, что другие ресурсы (сырье, электроэнергия и пр. ) не ограничены. Формализацию цели (достижение максимальной выручки цеха) мы обсудим позже.

Получим соотношения, следующие из условий ограниченности времени работы цеха и вместимости склада, т. е. суммарного числа изделий.

Из постановки задачи следует, что на изготовление одного пирожного затрачивается в 4 раза больше времени, чем на выпечку одного пирожка. Если обозначить время изготовления пирожка как t мин, то время изготовления пирожного будет равно 41 мин. Значит, суммарное время на изготовление х пирожков и у пирожных равно

tx + 4ty = (х + 4 y)t

Но это время не может быть больше длительности рабочего дня. Отсюда следует неравенство:

(х + 4y)t < = 8 * 60,
или
(х + 4y)t < = 480

Легко посчитать t — время изготовления одного пирожка. Поскольку за рабочий день их может быть изготовлено 1000 штук, то на один пирожок тратится 480/1000 = 0, 48 мин. Подставляя это значение в неравенство, получим:

(х + 4y) * 0, 48 < = 480.
Отсюда
х + 4у < = 1000

Ограничение на общее число изделий дает совершенно очевидное неравенство:

х + у < = 700

К двум полученным неравенствам следует добавить условия положительности значений величин х и у (не может быть отрицательного числа пирожков и пирожных). В итоге получим систему неравенств:

х + 4у < = 1000;
х + у < = 700;
х => 05
у => 0.

А теперь перейдем к формализации стратегической цели: получению максимальной выручки. Выручка — это стоимость всей проданной продукции. Пусть цена одного пирожка — г рублей. По условию задачи, цена пирожного в два раза больше, т. е. 2r рублей.

Отсюда стоимость всей произведенной за день продукции равна

rх + 2ry = r(х + 2у)

Целью производства является получение максимальной выручки. Будем рассматривать записанное выражение как функцию от х, у:

F(x, у) = r(х + 2 у)

Она называется целевой функцией.
Поскольку значение r — константа, то максимальное значение F(x, у) будет достигнуто при максимальной величине выражения (х + 2у). Поэтому в качестве целевой функции можно принять

f(x, у) = х + 2у

Следовательно, получение оптимального плана свелось к следующей математической задаче:
Требуется найти значения плановых показателей х и у, удовлетворяющих данной системе неравенств и придающих максимальное значение целевой функции.
Итак, математическая модель задачи оптимального планирования для школьного кондитерского цеха построена.

Теперь следующий вопрос: как решить эту задачу?

Вы уже догадываетесь, что решать ее за нас будет компьютер с помощью табличного процессора Excel. А мы обсудим лишь подход к решению, не вникая в подробности метода.

Математическая дисциплина, которая посвящена решению таких задач, называется математическим программированием. А поскольку в целевую функцию f(x, у) величины х и у входят линейно (т. е. в первой степени), то наша задача относится к разделу этой науки, который называется линейным программированием.

Система написанных выше неравенств представляется на координатной плоскости четырехугольником, ограниченным четырьмя прямыми, соответствующими линейным уравнениям:

х + 4у = 1000,
х + у = 700,
х = 0 (ось Y),
у = 0 (осьХ).

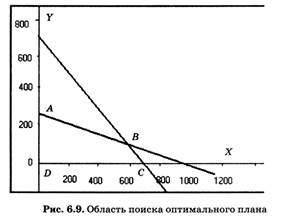
На рис. 6. 9 эта область представляет собой четырехугольник ABCD и выделена заливкой. Любая точка четырехугольника является решением системы неравенств.

Например, х = 200, у = 100.

Этой точке соответствует значение целевой функции f(200, 100) = 400. А другой точке

(х = 600, у = 50) соответствует f(600, 50) = 700. Но, очевидно, искомым решением является та точка области ABCD, в которой целевая функция максимальна. Нахождение этой точки производится с помощью методов линейного программирования.

В математическом арсенале Excel имеется средство Поиск решения. Как решать данную задачу с помощью этого средства, вы узнаете из компьютерного практикума.

В результате решения задачи получается следующий оптимальный план дневного производства кондитерского цеха: нужно выпускать 600 пирожков и 100 пирожных. Эти плановые показатели соответствуют координатам точки В на рис. 6. 9. В этой точке значение целевой функции f(600, 100) = 800. Если один пирожок стоит 5 рублей, то полученная выручка составит 4000 рублей.

Сегодня мы с вами узнали, что такое оптимальное планирование, получили представление о решении задач оптимального планирования, закрепили на практике знания и навыки работы с надстройкой «Поиск решения» в MS Excel, выработали навыки работы с задачами оптимального планирования в MS Excel.

Система основных понятий

Домашнее задание

Изучить §20, сделать краткий конспект. Разобрать задачу, решенную в конспекте. Писсьменно ответить на вопросы №1 (а, б) на стр. 131.