КЗ 17 (50). Сложение и умножение вероятностей.

Стр 1 из 2Следующая ⇒

КЗ 17 (50). Сложение и умножение вероятностей.

План

1. Теорема о сложении вероятностей.

2. Теорема об умножении вероятностей.

3. Задания для самостоятельной работы.

1. Теорема сложения вероятностей.

Вероятность наступления хотя бы одного из двух несовместных событий равна сумме их вероятностей. P(A+B) =P(A)+P(B).

Пример. В лотерее 1000 билетов; из них на один билет падает выигрыш 500 руб., на 100 билетов – выигрыши по 100 руб., на 50 билетов – выигрыши по 20 руб., на 100 билетов – выигрыши по 5 руб., остальные билеты невыигрышные. Некто покупает один билет. Найти вероятность выиграть не менее 20 руб.

Решение. Рассмотрим события:

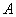– выиграть не менее 20 руб.,

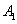- выиграть 20 руб.,

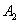- выиграть 100 руб.,

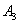- выиграть 500 руб.

Очевидно,

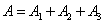По теореме сложения вероятностей

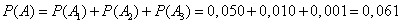Ответ: 0, 061.

Вероятность события 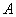, вычисленная при условии, что имело место другое событие 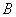, называется условной вероятностью события 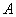и обозначается

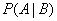2. Теорема умножения вероятностей.

Вероятность произведения двух событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную при условии, что первое имело место: .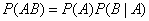

Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

Пример 1. В урне 2 белых и 3 черных шара. Из урны вынимают подряд два шара. Найти вероятность того, что оба шара белые.

Решение. Обозначим:

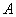- появление двух белых шаров.

Событие 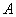представляет собой произведение двух событий:

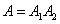где 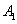- появление белого шара при первом вынимании, 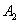- появление белого шара при втором вынимании.

По теореме умножения вероятностей

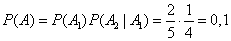Ответ: 0, 1.

Пример 2. Те же условия, но после первого вынимания шар возвращается в урну, и шары в урне перемешиваются.

Решение. В данном случае события 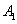и 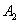независимы и

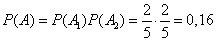Ответ: 0, 16.

12 Следующая ⇒