
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
01.04.22. тема: «Решение задач»
01. 04. 22. тема: «Решение задач»
1. Разобрать решение задачи № 232
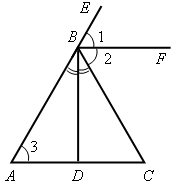
| Дано: 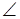 CВE – внешний угол треугольника АВС; CВE – внешний угол треугольника АВС; 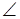 CВE = 2 CВE = 2 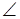 А.
Доказать: А.
Доказать: 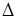 АВС – равнобедренный.
Решение
Проведем биссектрисы BF и ВD смежных углов СВЕ и АВС, тогда ВF АВС – равнобедренный.
Решение
Проведем биссектрисы BF и ВD смежных углов СВЕ и АВС, тогда ВF 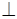 ВD (см. задачу № 83). ВD (см. задачу № 83).
|
ВF || АС, так как 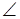 1=
1= 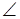 2 =
2 = 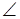 3, а углы 1 и 3 соответственные при пересечении прямых ВF и АС секущей АВ. ВD
3, а углы 1 и 3 соответственные при пересечении прямых ВF и АС секущей АВ. ВD 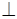 АС, так как ВD
АС, так как ВD 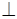 ВF, а ВF || АС. В треугольнике АВС биссектриса ВD является высотой, следовательно, треугольник АВС – равнобедренный (см. задачу № 133).
ВF, а ВF || АС. В треугольнике АВС биссектриса ВD является высотой, следовательно, треугольник АВС – равнобедренный (см. задачу № 133).
2. Обратное утверждение также верно, а именно: если треугольник равнобедренный, то внешний угол при вершине, противолежащей основанию треугольника, в два раза больше угла при основании.
Действительно, этот внешний угол равен сумме двух углов при основании равнобедренного треугольника, а так как углы при основании равны, то данный внешний угол в два раза больше угла при основании треугольника.
3. Решить задачу № 234 (рассмотреть два случая).
Домашнее задание: изучить пункты 30–31;
Решить задачи:
1. Один из углов равнобедренного треугольника равен 96°. Найдите два других угла треугольника.
2. В треугольнике СDЕ с углом 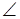 Е = 32° проведена биссектриса CF,
Е = 32° проведена биссектриса CF, 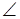 СFD = 72°. Найдите
СFD = 72°. Найдите 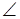 D.
D.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|