
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Образец экзаменационного задания
Образец экзаменационного задания
по дисциплине «Математика»
Специальности 210400. 62, 210200. 62, 201000. 62
2 курс, группы БРТ-21, БРС-21, ББС-21
Время экзамена 80 минут
Задания
№1. Градиентом функции 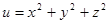 в точке М (2, -2, 1) является
в точке М (2, -2, 1) является
вектор {-2, 2, -1}
число 3
вектор {4, -4, 2}
число 6
№2. Производной функции 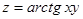 в точке Р (1, 1) в направлении биссектрисы первого координатного угла, является
в точке Р (1, 1) в направлении биссектрисы первого координатного угла, является
число 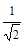
вектор {  ,
,  }
}
число 1
вектор {1, 1}
№3. Уравнение касательной плоскости к поверхности  в точке
в точке
М (1, 2, -1) имеет вид
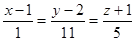
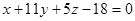
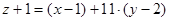
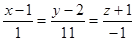
№4. Криволинейный интеграл по координатам 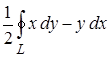 где
где 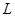 контур треугольника с вершинами
контур треугольника с вершинами  ,
,  и
и 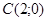 равен ###
равен ###
№5. Криволинейный интеграл по координатам ### равен нулю по любому замкнутому контуру.
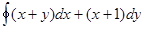
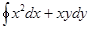
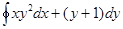
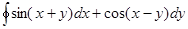
№6. Дано дифференциальное уравнение  . Тогда его решением является функция…
. Тогда его решением является функция…
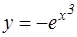
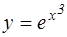
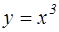
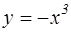
№7. Установите соответствие между дифференциальными уравнениями и способом их решения:
L1: 
L2: 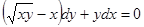
L3: 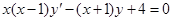
L4: 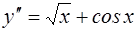
R1: разделение переменных
R2: замена переменной 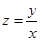 , где
, где 
R3: подстановка 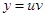 , где
, где 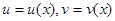
R4: двукратное интегрирование
№8. Однородному дифференциальному уравнению второго порядка 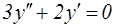 соответствует характеристическое уравнение
соответствует характеристическое уравнение


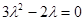
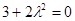
№9. Общим решением однородного дифференциального уравнения с постоянными коэффициентами и характеристическими корнями 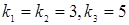 является…
является…
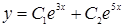
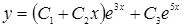

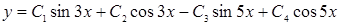
№10. Установите соответствие между дифференциальными уравнениями и их решениями:
L1: 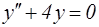
L2: 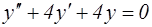
L3: 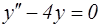
R1: 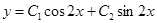
R2: 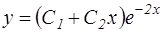
R3: 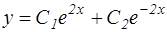
№11. Указать вид общего решения дифференциального уравнения 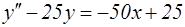 , если частным решением является функция
, если частным решением является функция 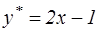
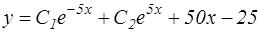
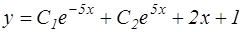

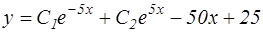
№12. Несовместные события А, В и С не образуют полную группу, если их вероятности равны
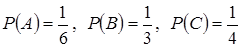
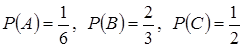
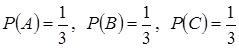
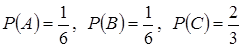
№13. Из урны, в которой находится 12 белых и 10 черных шаров, вынимают наудачу один шар. Тогда вероятность того, что этот шар будет черным, равна
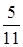
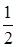
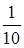

№14. На отрезок АВ длиной 12 см наугад «бросают» точку М. Попадание в любую точку отрезка равновероятно. Р – вероятностьтого, что длина отрезка АМ больше 6 см и меньше 9 см, тогда
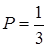
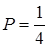
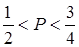

№15. Имеется 6 билетов в театр. Среди них 4 билета на места в первом ряду. Тогда вероятность того, что из трех наудачу выбранных билетов два окажутся на места первого ряда, равна
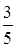
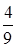
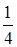
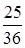
№16. Стрелок делает три выстрела по движущейся мишени. Вероятность одного попадания в мишень равна 0, 4; двух – 0, 15; трех – 0, 05. Установить соответствие между событиями и их вероятностями:
L1: «не менее двух попаданий в мишень»
L2: «хотя бы одно попадание в мишень»
L3: «ни одного попадания в мишень»
L4:
R1: 0, 2
R2: 0, 6
R3: 0, 4
R4: 0, 45
№17. Из урны, в которой находятся 6 черных и 10 белых шаров, вынимают один за другим два шара. Тогда вероятность того, что оба шара будут белыми, равна
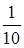
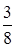
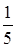
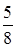
№18. Игральная кость бросается два раза. Тогда вероятность того, что число очков, равное двум, выпадет на верхней грани только один раз, равна

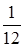
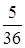

№19 С первого станка на сборку поступает 40%, со второго – 60% всех деталей. Среди деталей, поступивших с первого станка, 1% бракованных, со второго – 2% бракованных. Тогда вероятность того, что поступившая на сборку деталь бракованная, равна
0, 016
0, 03
0, 015
0, 014
№20. С первого станка на сборку поступает 60%, со второго – 40% всех деталей. Среди деталей, поступивших с первого станка, 70% стандартных, со второго – 90% стандартных. Взятая наудачу деталь оказалась стандартной. Тогда вероятность того, что она изготовлена на первом станке, равна
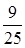
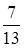
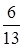
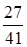
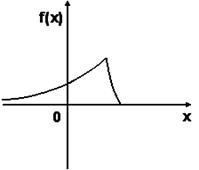
№21. График плотности вероятностей 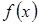 для нормального распределения изображен на рисунке
для нормального распределения изображен на рисунке
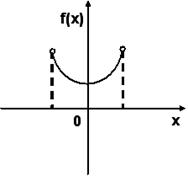
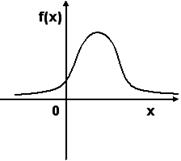
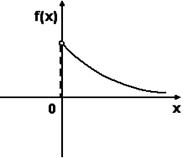
- 
№22. Дискретная случайная величина задана законом распределения вероятностей
 .
.
Тогда ее функция распределения вероятностей имеет вид
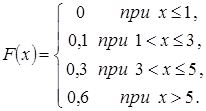
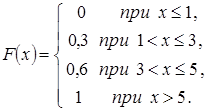
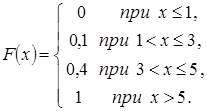
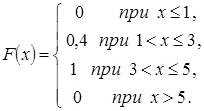
№23. Непрерывная случайная величина Х задана плотностью распределения вероятностей 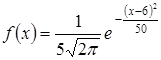 . Установите соответствие между числовыми характеристиками случайной величины Х и их значениями
. Установите соответствие между числовыми характеристиками случайной величины Х и их значениями
L1: математическое ожидание случайной величины Х
L2: дисперсия случайной величины Х
L3: среднее квадратичное отклонение случайной величины Х
L4:
R1: 6
R2: 25
R3: 5
R4: 50
№24. Производится п независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна 0, 2. Тогда математическое ожидание дискретной случайной величины Х – числа появлений события А в  проведенных испытаниях, равно
проведенных испытаниях, равно
№25. Изображение функции 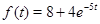 равно
равно
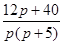
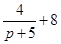
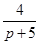
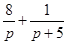
№26. Если  изображен, то его оригинал равен
изображен, то его оригинал равен
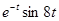
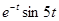
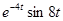
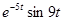
№27. Комплексное преобразование Фурье функции 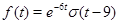 (
( 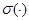 -- функция Хевисайда) равно
-- функция Хевисайда) равно
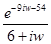
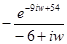
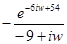
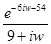
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|