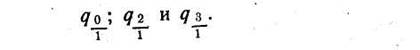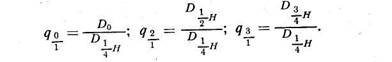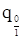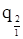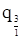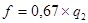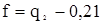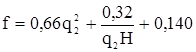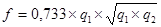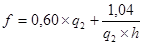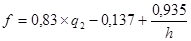Задание 4. Определение коэффициентов и классов формы, видовых чисел и отногсительных диаметров ствола

Задание 4. Определение коэффициентов и классов формы, видовых чисел и отногсительных диаметров ствола

Форма древесных стволов в зависимости от породы дерева и условий его роста варьирует, а это обстоятельство сказывается на объеме ствола. При одинаковых высотах и диаметрах на высоте 1, 3 м от основания ствола объемы стволов могут отличаться друг от друга в зависимости от их формы. Форма ствола является вместе с D_{1, 3} и Н основным объемообразующим фактором. Следовательно, форма стволов должна приниматься во внимание при практическом использовании имеющихся массовых таблиц и при составлении новых таблиц.

Форму стволов принято отображать коэффициентами и классами формы, видовыми числами и относительными диаметрами на относительных высотах.

К о э ф ф и ц и е н т ы формы q представляют собой отноше диаметра на любой высоте ствола к диаметру на высоте 1, 3 м от основания ствола. Наиболее употребительными являются:

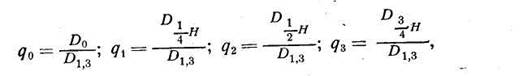
в которых наиболее важным бывает q₂

Видовое число ствола f — это отношение объема ствола к объему цилиндра, имеющего высоту, одинаковую со столом, и диаметр, равный диаметру ствола на высоте 1, 3 м от его основания. Между f, q₂ и Н ствола имеются определенные зависимости, позволяющие рассчитывать f, не прибегая к трудоемкому определению самого объема ствола. Если же будет известна величина видового числа f, то легко найти объем ствола, перемножая f на объем соответствующего цилиндра. В индивидуальных заданиях студенты рассчитывают как точное видовое число (f = V_ctb: V_цил), так и приближенные значения f по формулам, отражающим зависимость f, q₂ и Н.

Проф. А. В. Третьяков для характеристики формы ствола предложил использовать не коэффициенты, а так называемые классы формы ствола:

Классы формы рассчитывают по следующим формулам:

У классов формы есть определенное преимущество перед коэффициентами форумы: величина знаменателя при их расчете соответствует диаметрам, взятым на одинаковых относительных пысотах (Н/4) при любой высоте ствола, тогда как знаменателями в коэффициентах формы являются диаметры, взятые на постоянной высоте от основания ствола, а эта постоянная высота (1, 3 м) не является одинаковой долей от всей высоты при различных значениях последней.

Относительные диаметры на относительных высотах, предложенные проф. В. К. Захаровым, по своему содержанию аналогичны классам формы и имеют то же преимущество перед коэффициентами формы, что и классы. Но относительные диаметры более точно и детально, чем классы формы, характеризуют форму ствола и отдельных его частей. Поэтому они в последнее время все чаще используются при составлении таблиц объема и сбегов стволов. Однако относительные диаметры затруднительно применять в качестве выхода в таблицы. Расчет относительных диаметров на относительных высотах ведут следующим образом. Весь ствол по длине разбивается на 10 равных отрезков. Диаметр на 0, 1 высоты принимается за 100%, а диаметры на 0, 2; 0, 3; 0, 4; 0, 5; 0, 6; 0, 7; 0, 8 и 0, 9 высоты выражаются соответствующими процентами по отношению к D_{0, 1Н}.

Исходными данными для задания 4 служат те же обмеры ствола, которые использовались для выполнения трех первых заданий соответственно варианту, выданному каждому студенту.

Предварительно вычерчивают схему обмеров ствола, необходимых для расчетов коэффициентов и классов формы, видовых чисел и относительных диаметров. Объем ствола берется из выполненного задания 1 (рассчитанный по сложной формуле). Диаметры на 1/4Н, на 1/2Н, на 3/4H, а также на 0, 1, 0, 2, 0, 3 и т. д. высоты находят путем интерполяции на основе исходных данных. Коэффициенты и классы формы рассчитывают с точностью до 0, 01, видовые числа — до 0, 001, а относительные диаметры — до 0, 1%.

После выполнения расчетов делают заключение о сбежистости ствола, полагая, что к сильносбежистым относятся стволы, у которых q₂ и q_1/₂ меньше, чем соответственно 0, 65 и 0, 80, а к малосбежистым — стволы, у которых q₂ и q_1/₂ больше, чем соответственно 0, 75 и 0, 85.

Кроме того, студенты рассчитывают расхождения приближенных значений видового числа, установленного по эмпирическим формулам, с его точным значением и делают заключение о точности отдельных формул.

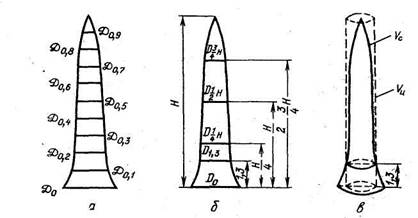
Рис. Схемы обмеров ствола:

а — для определения относительных диаметров; б — для определения коэффициентов и классов формы; в — для видовых чисел

Схемы обмеров ствола, необходимых для определения его коэффициентов и классов формы, видовых чисел и относительных диаметров, показаны на рис.

Определение коэффициентов и классов формы ствола дано в табл.:

Коэффициенты и классы формы		Расчет их величины
q₀	в коре	q₀=D₀: D _{1, 3}
q₀	без коры	q’₀=D’₀: D’ _{1, 3}
q₁	в коре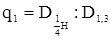
q₁	без коры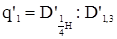
q₂	в коре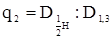
q₂	без коры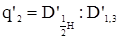
q₃	в коре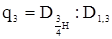
q₃	без коры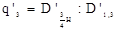
	в коре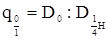
	без коры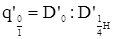
	в коре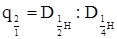
	без коры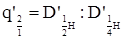
	в коре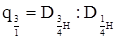
	без коры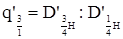

Определение видовых чисел дано в табл.:

Название способа расчета		Расчет
Точное (старое) видовое число	в коре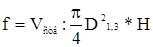
Точное (старое) видовое число	без коры
По формуле	в коре
По формуле	без коры
По формуле Гуттенберга	в коре
По формуле Гуттенберга	без коры
По формуле Кунце (1)	в коре
По формуле Кунце (1)	без коры
По формуле Шиффеля	в коре
По формуле Шиффеля	без коры
По формуле Третьякова	в коре
По формуле Третьякова	без коры
По формуле Шустова	в коре
По формуле Шустова	без коры
По формуле Козленко	в коре
По формуле Козленко	без коры
По формуле Кунце (2)	в коре
По формуле Кунце (2)	без коры
По таблице средних видовых чисел (по М. Е. Ткаченко)	в коре
По таблице средних видовых чисел (по М. Е. Ткаченко)	без коры

Расхождение приближенных значений f с его точным значением:

Способ	Абсолютное		В процентах
Способ	в коре	без коры	в коре	без коры
По формуле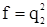
По формуле Гуттенберга
По формуле Кунце (1)
По формуле Шиффеля
По формуле Третьякова
По формуле Шустова
По формуле Козленко
По формуле Кунце (2)
По таблице М. Е. Ткаченко

Определение относительных диаметров ствола дано в табл.

Относи-тельные высоты ствола	Относительные диаметры ствола				Относи-тельные высоты ствола	Относительные диаметры ствола
	в коре		без коры			в коре		без коры
	см	%	см	%		см	%	см	%
0, 0 Н					0, 5 Н
0, 1 Н					0, 6 Н
0, 2 Н					0, 7 Н
0, 3 Н					0, 8 Н
0, 4 Н					0, 9 Н