Практическое занятие №62. Тема: «Исследование функций и построение их графиков с помощью производной». Алгоритм исследования функции с помощью производной. и построения ее графика. 2. Проверяем функцию на четность.. 4. Находим точки пересечения графика с

Практическое занятие №62

Тема: «Исследование функций и построение их графиков с помощью производной»

Задание №1. Еще разпройдите по ссылке и посмотрите примеры исследования функци и построение графиков с помощью производной (там я объясняю). Вспомните Алгоритм исследования функции (он должен быть у вас в тетрадях).

Алгоритм исследования функции с помощью производной

и построения ее графика

1. Находим область определения D(f) функции y = f(x).

2. Проверяем функцию на четность.

Если f(-x) = f(x), то функция четная, график функции симметричен относительно оси OY.

Если f(-x) = - f(x), то функция нечетная, график нечетной функции симметричен относительно начала координат.

В противном случае функция является ни четной, ни нечетной.

3. Если функция периодическая, то находим период функции.

4. Находим точки пересечения графика с осями координат.

Находим нули функции - это точки пересечения графика функции с осью абсцисс (Ox).

Для этого мы решаем уравнение f(x) = 0.

Находим точку пересечения графика функции с осью ординат (Oy). Для этого ищем значение функции при x=0.

5. Промежутки монотонности (возрастания и убывания функции)

Для этого мы следуем привычному алгоритму.

а) Находим производную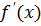

б) Приравниваем производную к нулю и находим критические точки функции ( 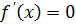и область определения производной)

Промежутки, на которых производная отрицательна, являются промежутками убывания функции.

Точки, в которых производная меняет знак с плюса на минус, являются точками максимума.

Точки, в которых производная меняет знак с минуса на плюс, являются точками минимума.

12 Следующая ⇒