
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
«Понятие о производной». Формулы и правила дифференцирования
15. 02. 2022
«Понятие о производной»
Задание №1. Разберите примеры вычисления производных в таблице. Перепишите в тетрадь таблицу полностью со всеми примерами (пояснения курсивом писать не нужно)
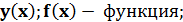
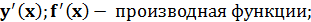
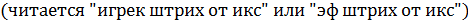
Формулы и правила дифференцирования
| № п/п | Формула | Пример |
| с' = 0 | 5' = 0; (-12) ' = 0; | |
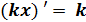
| (6x) ' = 6; (-7x) '=-7; 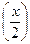 '= '= 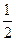 ; x' =1
В выражениях такого вида остается коэффициент (число), x отбрасывается ; x' =1
В выражениях такого вида остается коэффициент (число), x отбрасывается
| |
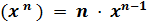
| (x17) ' = 17x16; (x8) ' = 8x7; (x -5) ' = -5x -6 В выражениях такого вида степень выносится вперед, х остается в степени на 1 меньше | |
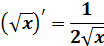
| ||
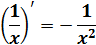
| ||
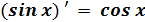
| ||
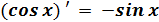
| ||
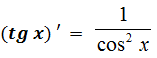
| ||
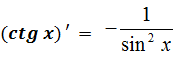
| ||
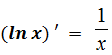
| ||
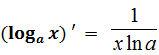
| ||
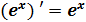
| ||
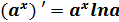
| ||
| Правила дифференцирования | Примеры | |
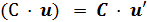
| (5x2) ' = 5 · 2x = 10x;
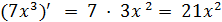 ; ;
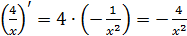 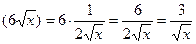 Коэффициент выписывается вперед и умножается на производную функции
Коэффициент выписывается вперед и умножается на производную функции
| |
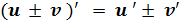
| 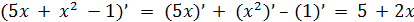
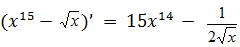 Если несколько функций складываются или вычитаются, то нужно по отдельности находить каждую производную, а затем их складывать или вычитать (в зависимости от знака)
Если несколько функций складываются или вычитаются, то нужно по отдельности находить каждую производную, а затем их складывать или вычитать (в зависимости от знака)
| |
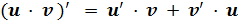
| (x3· 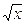 )' =(x3) '· )' =(x3) '· 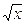 + ( + ( 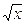 )'·x3=3x2· )'·x3=3x2· 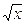 +
+ x3· +
+ x3· 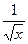
| |
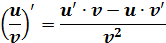
| 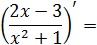
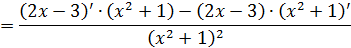
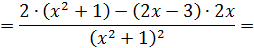
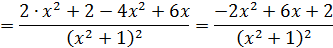
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|