Хелпикс

Главная

Контакты

Случайная статья



Площадь параллелограмма.



Площадь параллелограмма.

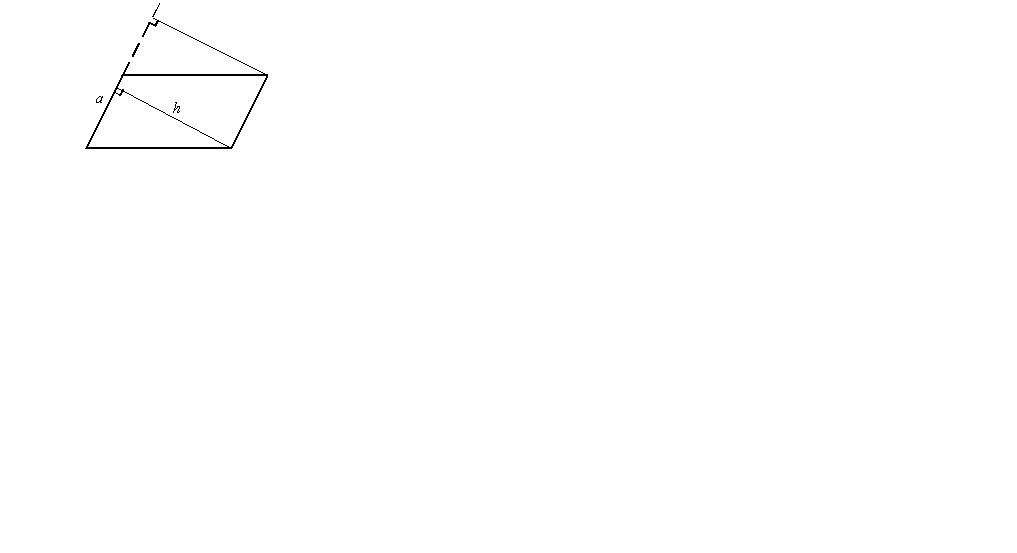Условимся одну из сторон параллелограмма называть основанием, а перпендикуляр, проведенный из любой точки противоположной стороны к прямой, содержащей основание, - высотой параллелограмма.

 

Теорема.

Площадь параллелограмма равна произведению его основания на высоту.

Дано: ABCD – параллелограмм. S – площадь параллелограмма.

Доказать: S = AD· BH.

Доказательство: AD – основание, BH – высота, СК – высота.

I) Трапеция АВСК составлена из параллелограмма ABCD и 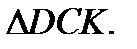С другой стороны, она составлена из прямоугольника ВНКС  и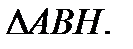

II) Рассмотрим 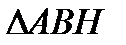  и 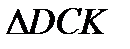 (они прямоугольные).

1) 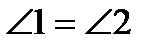(соответственные при параллельных прямых АВ и CD и секущей АК).

2) АВ = СD (по свойству параллелограмма).

Из условий 1), 2) получаем, что 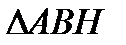 =  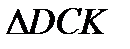по гипотенузе и острому углу. Значит,  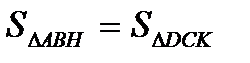(по свойству площади).

III) Из I и II получаем, что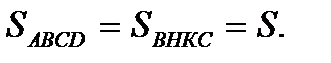

IV) 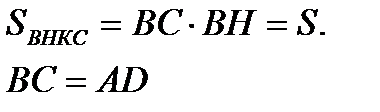    Тогда 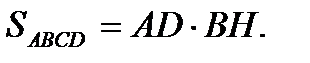                                       Что и требовалось доказать.

 



  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.