Фигуры вращения и площади их поверхностей.

Фигуры вращения и площади их поверхностей.

Цель работы:

Корректировать знания, умения и навыки по теме: «Фигуры вращения и площади их поверхностей».
Закрепить и систематизировать знания по теме.
Определить уровень усвоения знаний, оценить результат деятельности студентов.

1. Необходимый теоретический материал

Конус, цилиндр и шар — это тела вращения. Они так называются, потому что их можно получить, вращая определенную фигуру вокруг некоторой оси.

Цилиндром называется тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Эти круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки оснований, — образующими цилиндра.

Если образующие перпендикулярны основаниям, то цилиндр называется прямым цилиндром.

Мы будем рассматривать только прямые цилиндры. Прямой цилиндр можно получить, если вращать прямоугольник вокруг одной из его сторон.

Высота цилиндра — это отрезок, соединяющий основания и перпендикулярный основаниям цилиндра.

Каждая образующая прямого цилиндра равна высоте.

Конец формы

Следующий важнейший пример тела вращения — это шар.

Шар — тело, состоящее из всех точек пространства, находящихся на расстоянии не более R от некоторой точки, которая называется центром шара. R называется радиусом шара.

Сфера — это поверхность шара. Сфера является множеством точек, отстоящих от ее центра на расстояние R.

Шар можно получить вращением полукруга вокруг его диаметра, а сферу – вращением полуокружности вокруг её диаметра.

Конус — это тело, которое получается при объединении всех отрезков, соединяющих точки круга (основание конуса) с вершиной конуса.

Прямой конус — это конус, вершина которого лежит на прямой, перпендикулярной основанию и проходящей через центр основания. Эта прямая называется осью прямого конуса.

Высота конуса — это отрезок, проведенный из вершины конуса к основанию перпендикулярно основанию конуса. Отрезок, который соединяет вершину конуса с окружностью в основании, называется образующей конуса.

Прямой конус можно получить вращением прямоугольного треугольника вокруг одного из его катетов.

Площади тел вращения:

Площадь боковой поверхности цилиндра 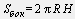Площадь полной поверхности цилиндра
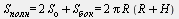
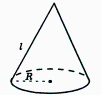
Площадь боковой поверхности конуса 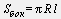Площадь полной поверхности конуса
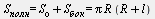
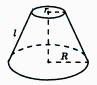
Площадь боковой поверхности усеченного конуса 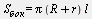Площадь полной поверхности усеченного конуса
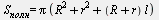
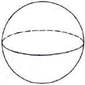
Площадь поверхности сферы

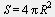
2. Решить:

1. Сечение шара плоскостью имеет площадь 36 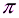(м 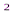). Радиус шара 10м. Найти расстояние от центра шара до плоскости сечения.

2. Площадь боковой поверхности цилиндра равна 72π, а диаметр основания — 9. Найдите высоту цилиндра.

3. Высота конуса равна 57, а диаметр основания — 152. Найдите образующую конуса.