
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Теорема. Площадь трапеции равна произведению полусуммы её оснований на высоту.
 Теорема Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Теорема Пифагора.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
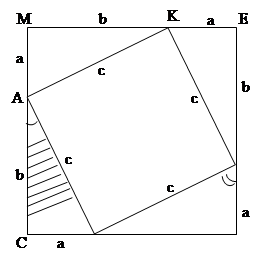
SСАВ = SМКА = SЕDК = SFBD =
4) AB = KA = DK = BD = c (соответственные стороны в равных треугольниках), значит AKDB - ромб;
Получаем, что AKDB – квадрат.
5) SСМЕF = (а + b)2. SСМЕF = 4SСАВ + SКАBD = 4· (а + b)2 = 2ab + c2 a2 + 2ab + c2 = 2ab + c2, а2 + b2 = с2. Ч. т. д. | Теорема обратная теореме Пифагора.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
2) Рассмотрим А1В1 = АВ, А1С1 = АС, В1С1= ВС,
3) Ч. т. д. Теорема. Площадь трапеции равна произведению полусуммы её оснований на высоту.
3) BH = DH1( расстояние между BC||AD) 4). SABCD = SABD + SDCВ = = Ч. т. д. |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|



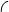

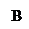
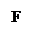
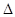 АВС,
АВС, 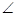 С = 900, АВ = с, АС = b, ВС = а.
Доказать: а2 + b2 = с2.
Доказательство:
1) Достроим
С = 900, АВ = с, АС = b, ВС = а.
Доказать: а2 + b2 = с2.
Доказательство:
1) Достроим 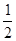 ab.
ab. 


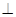 AD, ВH = h.
Доказать: SABCD =
AD, ВH = h.
Доказать: SABCD =