
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Действительные числа
Все рациональные и иррациональные числа образуют множество действительных ( вещественных ) чисел. Множество всех действительных чисел обозначают буквой R. Очевидно, что R 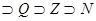 .
.
Основные свойства действительных чисел:
1. множество действительных чисел упорядоченное, то есть для каждых двух различных действительных чисел 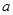 и
и 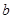 можно указать, какое из них меньшее;
можно указать, какое из них меньшее;
2. множество действительных чисел всюду плотное, то есть между каждыми двумя действительными числами 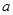 и
и 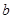
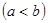 существует еще по крайней мере одно действительное число
существует еще по крайней мере одно действительное число 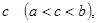 а следовательно, и бесконечное множество действительных чисел;
а следовательно, и бесконечное множество действительных чисел;
3. множество действительных чисел непрерывно, то есть в множестве действительных чисел нет ни скачков, ни пробелов, а геометрически это означает, что каждому действительному числу 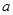 на числовой прямой соответствует точка, имеющая координату
на числовой прямой соответствует точка, имеющая координату 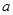 , и, обратно, каждая точка числовой прямой имеет действительную координату;
, и, обратно, каждая точка числовой прямой имеет действительную координату;
4. арифметические действия над действительными числами всегда возможны (кроме деления на нуль) и в результате дают действительное число.
Множество действительных чисел R дополняют двумя элементами, обозначаемыми 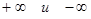 (плюс и минус бесконечность). При этом полагают, что
(плюс и минус бесконечность). При этом полагают, что 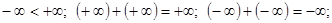
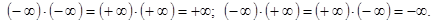
Но операции 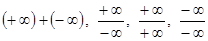 не определены. Кроме того, для любого числа
не определены. Кроме того, для любого числа 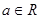 полагают, что справедливо неравенство
полагают, что справедливо неравенство 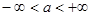
и справедливы операции 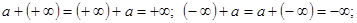
для 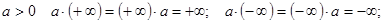
для 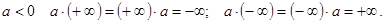
Операции 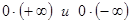 не определены. Бесконечности
не определены. Бесконечности 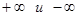 называют иногда «бесконечными числами» в отличие от действительных чисел, которые называют «конечными числами». В дальнейшем под числом будем понимать конечное число.
называют иногда «бесконечными числами» в отличие от действительных чисел, которые называют «конечными числами». В дальнейшем под числом будем понимать конечное число.
Определение 1. Абсолютной величиной, или модулем, действительного числа 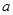 называют неотрицательное число обозначаемое
называют неотрицательное число обозначаемое 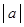 и определяемое следующим образом:
и определяемое следующим образом:
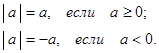
Ясно, что 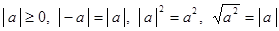 . Если
. Если 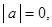 то это эквивалентно тому, что
то это эквивалентно тому, что 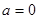 . Для любых действительных чисел
. Для любых действительных чисел 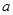 и
и 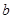 справедливы следующие соотношения:
справедливы следующие соотношения:
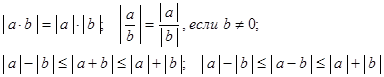
Определение 2. Подмножество 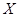 множества всех действительных чисел
множества всех действительных чисел 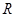 называется ограниченным снизу, если существует действительное число
называется ограниченным снизу, если существует действительное число 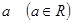 такое, что оно не больше каждого числа
такое, что оно не больше каждого числа  из X, то есть для любого
из X, то есть для любого 
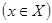 выполняется неравенство
выполняется неравенство 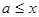 . Число
. Число 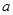 называют числом, ограничивающим множество
называют числом, ограничивающим множество 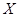 снизу.
снизу.
Множество, не являющиеся множеством ограниченным снизу, называют множеством неограниченным снизу. Термин «множество неограниченное снизу» означает, что каково бы ни было отрицательное, сколь угодно большое по абсолютной величине число 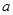 , в данном множестве обязательно найдется еще меньшее число
, в данном множестве обязательно найдется еще меньшее число 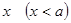 .
.
Если множество 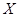 ограничено снизу числом
ограничено снизу числом 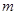 , и число
, и число 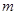 принадлежит множеству
принадлежит множеству 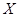
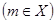 , то число
, то число 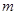 называют наименьшим или минимальным числом множества
называют наименьшим или минимальным числом множества 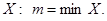 Если в множестве есть наименьшее число, то оно единственно.
Если в множестве есть наименьшее число, то оно единственно.
Пример. а) множество чисел 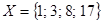 ограничено снизу числом 1, причем это число 1 является наименьшим;
ограничено снизу числом 1, причем это число 1 является наименьшим;
б) множество X – множество всех неотрицательных чисел 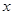 (т. е. чисел, удовлетворяющих неравенству
(т. е. чисел, удовлетворяющих неравенству 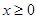 ) тоже является ограниченным снизу и его наименьшим значением является число
) тоже является ограниченным снизу и его наименьшим значением является число  ;
;
в) множество Y – множество всех положительных чисел  (т. е. чисел, удовлетворяющих неравенству
(т. е. чисел, удовлетворяющих неравенству 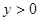 ) тоже является ограниченным снизу числом
) тоже является ограниченным снизу числом  , но множество Y не имеет наименьшего, так как число
, но множество Y не имеет наименьшего, так как число  не принадлежит Y. При этом число
не принадлежит Y. При этом число  является наибольшим из всех чисел, ограничивающих множество Y снизу, а элементы
является наибольшим из всех чисел, ограничивающих множество Y снизу, а элементы  множества Y в силу свойств плотности и непрерывности действительных чисел могут быть сколь угодно близки к числу
множества Y в силу свойств плотности и непрерывности действительных чисел могут быть сколь угодно близки к числу  , оставаясь больше его;
, оставаясь больше его;
г) множество D – множество всех отрицательных чисел неограниченно снизу, так как какое бы отрицательное число ни взять, найдется еще меньше число.
Определение 3. Подмножество 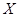 множества всех действительных чисел
множества всех действительных чисел 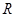 называется ограниченным сверху, если существует такое число
называется ограниченным сверху, если существует такое число 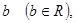 что оно не меньше каждого числа
что оно не меньше каждого числа 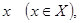 то есть для любого
то есть для любого 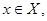 выполняется неравенство
выполняется неравенство 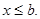 Число
Число 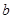 называют числом ограничивающим множество
называют числом ограничивающим множество 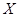 сверху.
сверху.
Множество, не являющееся множеством ограниченным сверху, называют множеством неограниченным сверху. Термин «множество неограниченное сверху» означает, что каково бы ни было сколь угодно большое положительное число 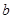 , в данном множестве обязательно найдется еще большее число.
, в данном множестве обязательно найдется еще большее число.
Если множество 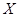 ограничено сверху числом
ограничено сверху числом 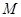 и
и 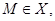 то число
то число 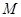 называют наибольшим или максимальным числом множества
называют наибольшим или максимальным числом множества 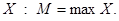 Если есть в множестве наибольшее число, то оно единственное.
Если есть в множестве наибольшее число, то оно единственное.
Определение 4. Множество, ограниченное и снизу и сверху, называется ограниченным множеством.
Другими словами, множество 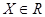 ограничено, если существуют числа
ограничено, если существуют числа 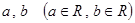 такие, что для каждого
такие, что для каждого 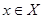 справедливо неравенство:
справедливо неравенство: 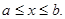
Множество, не являющееся ограниченным, называют неограниченным.
Пример. а) множество 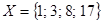 ограничено, т. к. для всякого
ограничено, т. к. для всякого 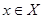 справедливо
справедливо 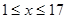 , причем оно имеет и наименьшее значение
, причем оно имеет и наименьшее значение 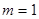 и наибольшее
и наибольшее 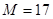 ;
;
б) множество 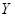 - множество положительных чисел, являясь ограниченным снизу, неограниченно сверху,
- множество положительных чисел, являясь ограниченным снизу, неограниченно сверху, 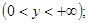
в) множество 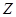 - множество всех целых чисел неограниченно как снизу, так и сверху
- множество всех целых чисел неограниченно как снизу, так и сверху 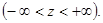
Ясно, что чисел ограничивающих множество снизу (сверху) может быть много.
Определение 5. Наибольшее число среди всех чисел, ограничивающих снизу множество 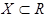 , называется нижней гранью (или инфимумом ) множества
, называется нижней гранью (или инфимумом ) множества 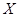 и обозначается через
и обозначается через 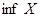 (инфимум - от латинского слова infimum – наименьший).
(инфимум - от латинского слова infimum – наименьший).
Например, для множества 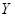 - множества всех положительных чисел нижней гранью является число 0, а для множества всех натуральных чисел
- множества всех положительных чисел нижней гранью является число 0, а для множества всех натуральных чисел 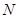 нижней гранью является число 1, оно является и наименьшим.
нижней гранью является число 1, оно является и наименьшим.
Определение 6. Наименьшее среди всех чисел, ограничивающих сверху множество 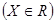 , называется верхней гранью (или супремумом ) множества
, называется верхней гранью (или супремумом ) множества 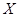 и обозначается через
и обозначается через 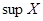 (супремум – от латинского слова supremum – наибольший).
(супремум – от латинского слова supremum – наибольший).
Например, для множества всех отрицательных чисел число 0 является верхней гранью.
Если в множестве существует наименьшее (наибольшее) число, то оно является нижней (верхней) гранью этого множества. Всякое ограниченное сверху непустое множество имеет верхнюю грань, а всякое ограниченное снизу непустое множество имеет нижнюю грань.
Множество всех действительных чисел 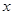 , удовлетворяющих двойному неравенству
, удовлетворяющих двойному неравенству 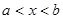 , называют открытым промежутком или интервалом и обозначают
, называют открытым промежутком или интервалом и обозначают 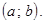
Множество всех действительных чисел 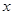 , удовлетворяющих двойному неравенству
, удовлетворяющих двойному неравенству 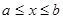 , называют закрытым промежутком или отрезком и обозначают
, называют закрытым промежутком или отрезком и обозначают 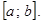
Пример 5. Примеры числовых множеств:
1. 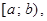 если
если 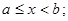 2.
2. 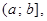 если
если 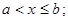
3. 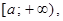 если
если 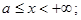 4.
4. 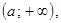 если
если 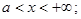
5. 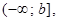 если
если 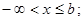 6.
6. 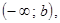 если
если 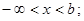
7. 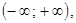 если
если 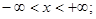 8.
8. 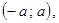 если
если 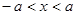
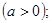
9. 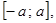 если
если 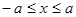
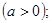 10.
10. 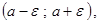 если
если 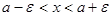
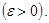
Множества, приведенные под номерами 1и 2, называют полуоткрытыми промежутками, множества под номерами 3, 4, 5, 6, 7 называют неограниченными промежутками, причем множество под номером 7есть множество всех действительных чисел R.
Определение 7. Множество всех действительных чисел 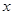 , удовлетворяющих двойному неравенству
, удовлетворяющих двойному неравенству 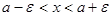 , где
, где 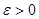 , называют e - окрестностью точки a .
, называют e - окрестностью точки a .
Этот факт можно записать следующим образом 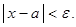 Для любых двух неравных действительных чисел
Для любых двух неравных действительных чисел 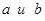 существуют непересекающиеся
существуют непересекающиеся  - окрестности.
- окрестности.
Числовое множество 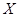 называютсимметричным относительно начала координат, если этому множеству вместе с числом
называютсимметричным относительно начала координат, если этому множеству вместе с числом 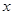 принадлежит и ему противоположное число
принадлежит и ему противоположное число 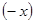 , то есть, если
, то есть, если 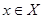 , то и
, то и 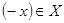 .
.
Примерами таких множеств являются множества под номерами 7, 8, 9, а так же множество всех рациональных чисел Q и множество 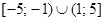 и т. д.
и т. д.
Вопросы и задания
1. Записать определения ограниченного снизу, ограниченного сверху, ограниченного множества. Привести примеры таких множеств. Что такое наименьшее (наибольшее) число множества?
2. Дать опеределение нижней грани (инфимума), верхней грани (супремума).
3. Что такое e - окрестность точки a? Изобразить на числовой прямой 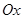 e - окрестность точек A(2), В(3) так, чтобы они: а) не пересекались; б) пересекались. Указать возможные значения e для каждого из случаев.
e - окрестность точек A(2), В(3) так, чтобы они: а) не пересекались; б) пересекались. Указать возможные значения e для каждого из случаев.
4. Перечислить операции с 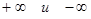 , которые не определены.
, которые не определены.
5. Даны множества 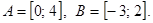 Указать наименьшее и наибольшее числа каждого из множеств: а)
Указать наименьшее и наибольшее числа каждого из множеств: а) 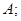 б)
б) 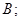 в)
в) 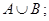 г)
г) 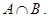
6. Даны множества 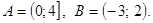 Указать точные нижние грани (инфимумы) и точные верхние грани (супремумы) множеств: а)
Указать точные нижние грани (инфимумы) и точные верхние грани (супремумы) множеств: а) 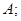 б)
б) 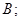 в)
в) 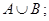 г)
г) 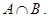 Имеют ли эти множества наименьшее и наибольшее числа?
Имеют ли эти множества наименьшее и наибольшее числа?
7. Даны множества 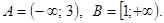 Имеют ли эти множества точные нижние и верхние грани, наименьшее и наибольшее числа? Если имеют, то указать их.
Имеют ли эти множества точные нижние и верхние грани, наименьшее и наибольшее числа? Если имеют, то указать их.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|