В.В.Бурляев. ЧИСЛЕННЫЕ МЕТОДЫ. в примерах на EXCEL

Московская Государственная Академия Тонкой Химической Технологии

им. М. В. Ломоносова

В. В. Бурляев

ЧИСЛЕННЫЕ МЕТОДЫ

в примерах на EXCEL

Методическое пособие по дисциплине

“Применение информационных технологий

в химии и химической технологии”

под редакцией профессора В. Ф. Корнюшко

Москва

1999 г.

ББК 32. 97

УДК 681. 3

БУРЛЯЕВ В. В.

Численные методы в примерах на EXCEL.

Методическое пособие по дисциплине “Применение информационных технологий в химии и химической технологии”, 2 изд., испр. и доп., МИТХТ, 1999, с. 63.

Под редакцией проф. Корнюшко В. Ф.

Рецензент - д. т. н., профессор Бахвалов Л. А.

Пособие предназначено для самостоятельного изучения раздела дисциплины “Применение информационных технологий в химии и химической технологии”, изучаемой в МИТХТ на втором году обучения для всех направлений бакалавриата, при подготовке к выполнению лабораторных работ. Оно должно дать студенту основные понятия о численных методах вычислительной математики с использованием современных компьютеров и доступных программных средств.

Основное внимание уделено тщательно подобранным примерам, позволяющим наиболее ярко проиллюстрировать те или иные особенности каждого метода. Все примеры выполнены на одном из самых мощных современных программных средств - табличном процессоре EXCEL, входящим в состав широко распространенного пакета MICROSOFT OFFICE.

Пособие охватывает все темы раздела учебной программы указанной дисциплины. Кроме методов, входящих в учебную программу, в пособии описаны алгоритмы и вычислительные процедуры встроенных в EXCEL специальных подпрограмм и функций, позволяющих реализовать те или иные численные методы, например, матричные вычисления, линейный регрессионный анализ, метод сопряженных градиентов, линейное программирование и т. п.

По сравнению с первым изданием 1997 г. содержание пособия приведено в соответствие с Государственным образовательным стандартом, исправлены опечатки и стилистические неточности.

СОДЕРЖАНИЕ

1. РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ с одним неизвестным. 5

1. 1 Отделение корней.................................................................................................. 5

Пример 1. 1.................................................................................................................... 5

1. 2 Уточнение корней: метод итераций.................................................................... 6

Пример 1. 2.................................................................................................................... 7

1. 3 Уточнение корней: метод Ньютона..................................................................... 8

Пример 1. 3.................................................................................................................... 9

1. 4. Уточнение корней: метод бисекции ( деления отрезка пополам )................ 10

Пример 1. 4.................................................................................................................. 10

1. 5 Уточнение коней: подпрограмма EXCEL “Подбор параметра”................... 12

2. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ................. 13

2. 1. Матричный метод............................................................................................... 13

Пример 2. 1.................................................................................................................. 14

2. 2. Метод приближенных вычислений.................................................................. 15

Пример 2. 2.................................................................................................................. 16

2. 3. Метод Гаусса – Зайделя...................................................................................... 18

Пример 2. 3.................................................................................................................. 18

3. РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.................................. 20

3. 1. Выбор начальных приближений....................................................................... 20

Пример 3. 1.................................................................................................................. 20

3. 2 Метод Ньютона.................................................................................................... 21

Пример 3. 2.................................................................................................................. 22

3. 3. Метод итераций.................................................................................................. 23

Пример 3. 3.................................................................................................................. 24

4. ЧИСЛЕННЫЕ МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ..................... 25

4. 1. Метод дихотомии................................................................................................ 25

Пример 4. 1.................................................................................................................. 26

4. 2. Метод золотого сечения..................................................................................... 27

Пример 4. 2.................................................................................................................. 28

4. 3. Встроенная подпрограмма EXCEL “Поиск решения”.................................... 29

5. МНОГОМЕРНЫЕ ЗАДАЧИ ОПТИМИЗАЦИИ................................................ 30

5. 1. Безусловная оптимизация: метод покоординатного спуска.......................... 30

Пример 5. 1.................................................................................................................. 31

5. 2. Безусловная оптимизация: метод наискорейшего спуска.............................. 32

Пример 5. 2.................................................................................................................. 33

5. 3. Безусловная оптимизация: подпрограмма EXCEL “Поиск решения”.......... 35

5. 4. Условная оптимизация: метод штрафных функций....................................... 35

Пример 5. 3.................................................................................................................. 37

5. 5. Условная оптимизация: подпрограмма EXCEL “Поиск решения”............... 38

5. 6. Условная оптимизация: линейное программирование.................................. 39

Пример 5. 4.................................................................................................................. 39

6. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ........................................................... 43

Пример 6. 1.................................................................................................................. 44

Пример 6. 2.................................................................................................................. 45

7. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ..................................... 48

Пример 7. 1.................................................................................................................. 49

8. ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ 51

8. 1. Метод Эйлера...................................................................................................... 51

Пример 8. 1.................................................................................................................. 51

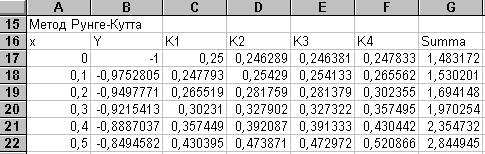
8. 2. Метод Рунге-Кутта четвертого порядка........................................................... 52

Пример 8. 2.................................................................................................................. 53

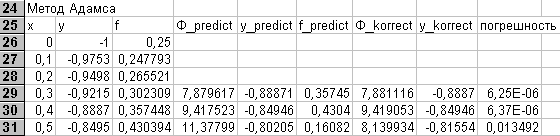
8. 3. Метод прогноза и коррекции: метод Адамса................................................... 53

Пример 8. 3.................................................................................................................. 54

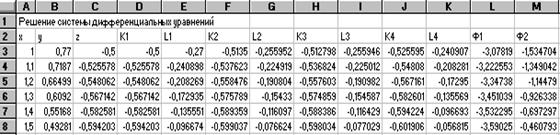
9. РЕШЕНИЕ СИСТЕМ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ. 55

9. 1. Задача Коши........................................................................................................ 55

Пример 9. 1.................................................................................................................. 56

9. 2. Краевая задача: метод стрельбы........................................................................ 57

Пример 9. 2.................................................................................................................. 57

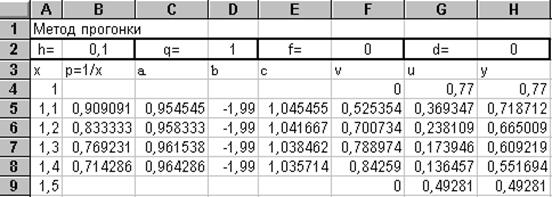
9. 3. Краевая задача: метод прогонки........................................................................ 57

Пример 9. 3.................................................................................................................. 58

10. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ 60

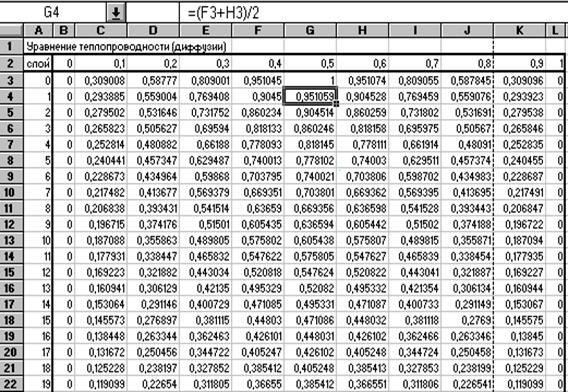
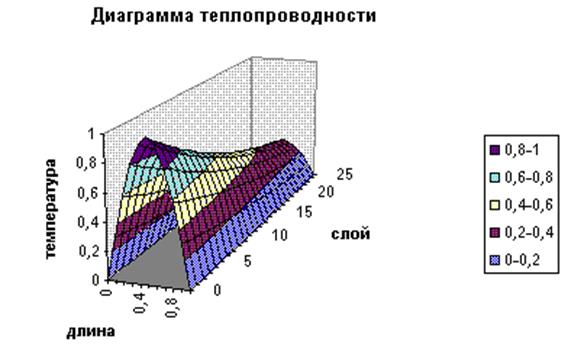
Пример 10. 1................................................................................................................ 61

1. РЕШЕНИЕ НЕЛИНЕЙНОГО УРАВНЕНИЯ с одним неизвестным.

Уравнение с одним неизвестным можно записать в каноническом виде

f(x) = 0

Решение уравнения заключается в нахождении корней, т. е. таких значений х, которые обращают уравнение в тождество. В зависимости от того, какие функции входят в уравнение, разделяют два больших класса уравнений - алгебраические и трансцендентные. Функция называется алгебраической, если для получения значения функции по данному значению х нужно выполнить арифметические операции и возведение в степень. К трансцендентным функциям относятся показательная, логарифмическая, тригонометрические прямые и обратные и т. п.

Найти точные значения корней можно лишь в исключительных случаях. Как правило, используются методы приближенного вычисления корней с заданной степенью точности Е. Это означает, что если установлено, что искомый корень лежит внутри интервала [a, b], где a - левая граница, а b - правая граница интервала, и длина интервала (b-a) < = E, то за приближенное значение корня можно принять любое число, находящееся внутри этого интервала.

Процесс нахождения приближенных значений корней разбивается на два этапа: 1) отделение корней и 2) уточнение корней до заданной степени точности. Рассмотрим эти этапы подробнее.

1. 1 Отделение корней.

Любой корень уравнения считается отделенным на отрезке [a, b], если на этом отрезке исследуемое уравнение не имеет других корней.

Отделить корни - это значит разбить всю область допустимых значений х на отрезки, в каждом из которых содержится только один корень. Эту операцию можно провести двумя способами - графическим и табличным. Если функция f(x) такова, что можно легко построить качественный график ее изменения, то по этому графику достаточно грубо находятся два числа, между которыми лежит одна точка пересечения функции с осью абсцисс. Иногда с целью облегчения построения, целесообразно представить исходное каноническое уравнение в виде f₁(x) = f₂(x), затем построить графики этих функций, причем абсциссы пересечения графиков и служат корнями данного уравнения.

При наличии компьютера наиболее распространен табличный способ отделения корней. Он заключается в табулировании функции f(x) при изменении х от некоторого значения х_нач до значения х_кон с шагом dx. Задача заключается в том, чтобы найти в этой таблице такие два смежных значения х, для которых функция имеет разные знаки. Предположим, что такие два значения a и b=a+dx найдены, т. е. f(a)*f(b)< 0. Тогда согласно теореме Больцано-Коши внутри отрезка [a, b], если функция f(x) непрерывна, существует точка с, в которой f(c)=0. EXCEL позволяет легко реализовать оба способа отделения корней. Рассмотрим их на примере.

Пример 1. 1.

Требуется отделить корни уравнения

e^x-10x = 0

Для этого надо протабулировать функцию f(Х) = exp(Х) - 10*Х, записанную по правилам EXCEL, и построить ее график при изменении Х от какого-то Х_начдо Х_кон с шагом dХ. Пусть эти значения сначала будут таковы: Х_нач = 0, Х_кон = 5, dХ = 0, 5. Если в этих пределах изменения Х нам не удастся отделить ни одного корня, тогда надо будет задать новые начальное и конечное значения х и, может быть, изменить шаг.

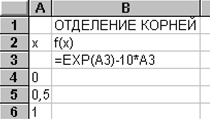
Для построения таблицы целесообразно воспользоваться специальной подпрограммой ТАБЛИЦА. Для этого на новом рабочем листе в ячейке B1 введем текст: ОТДЕЛЕНИЕ КОРНЕЙ. Затем в ячейку А2 введем текст: x, а в смежную ей ячейку В2 - текст: f(x). Далее оставим ячейку А3 пустой, но в ячейку В3 введем формулу исследуемой функции по правилам EXCEL, а именно

=EXP(A3)-10*A3

Затем заполним числовой ряд изменений X в строках А4: A14 от 0 до 5 с шагом 0, 5.

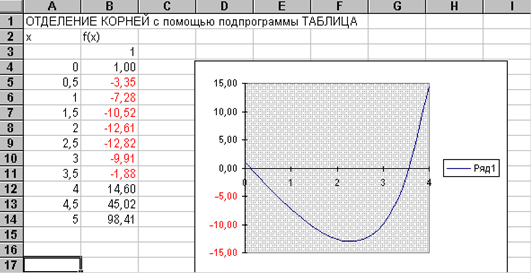
Выделим блок ячеек А3: B14. Теперь дадим команду меню Данные- Таблица. Результаты табулирования будут помещены в блок ячеек В4: В14. Для того чтобы сделать их более наглядными, нужно отформатировать блок В4: B14 так, чтобы отрицательные числа окрашивались в красный цвет. В этом случае легко найти два смежных значения X, для которых значения функции имеют разные знаки. Их и надо принять за концы интервала отделения корней. В нашем случае таких интервалов, как видно из таблицы два - [0; 0, 5] и [ 3, 5; 4].

Далее следует построить график нашей функции, выделив блок А4: B14 и вызвав Мастер Диаграмм. В результате получим на экране диаграмму изменения f(X), из которой видны следующие интервалы отделения корней [0; 1] и [3; 4].

Если изменять теперь числовые значения х в блоке А4: A14 то значения функции в ячейках B4: B14и график будут изменяться автоматически.

1. 2 Уточнение корней: метод итераций.

Для уточнения корня методом итераций должно быть задано:

1) уравнение f(X) = 0, причем f(X) должно быть задано в виде формулы,

2) числа a - левая граница и b - правая граница интервала, внутри которого лежит один корень,

3) число Е - заданная точность получения корня.

Сам метод можно разбить на два этапа:
а) переход от канонического вида записи уравнения f(X)=0 к итерирующему виду X = g(X),
б) вычислительная итерирующая процедура уточнения корня.

Перейти от канонического вида уравнения к итерирующему можно различными способами, важно лишь чтобы при этом выполнялось достаточное условие сходимости метода: ç g’(X)ç < 1 на [a, b], т. е. модуль первой производной итерирующей функции должен быть меньше 1 на интервале [a, b]. Причем чем меньше этот модуль, тем больше скорость сходимости.

Вычислительная процедура метода состоит в следующем. Выбираем начальное приближение, обычно равное Х₀= (a+b)/2. Затем вычислим X₁=g(X₀) и D= X₁- X₀. Если модуль D < = E, то X₁ является корнем уравнения. В противном случае переходим ко второй итерации: вычисляем Х₂=g(X₁) и новое значение D=X₂- X₁. Опять проводим проверку на точность и при необходимости продолжаем итерации. Если g(X) выбрано правильно и удовлетворяет достаточному условию сходимости, то эта итерирующая процедура сойдется к корню. Следует отметить, что от знака g’(X) зависит характер сходимости: при g’(X)> 0 сходимость будет монотонной, т. е. с увеличением итераций D будет приближаться к Е монотонно (не меняя знака), в то время как при g’(X)< 0 сходимость будет колебательной, т. е. D будет приближаться к Е по модулю, меняя знак на каждой итерации.

Рассмотрим реализацию метода итераций на EXCEL на примере.

Пример 1. 2

Уточним методом итераций значение корней, отделенных в примере 2. 1. Итак пусть f(X)= exp(X) - 10*X, для первого корня a=0 и b=0, 5. Пусть Е=0, 00001. Как выбрать итерирующую функцию? Например, так g(X)=0, 1*exp(X). На интервале [a, b] ç g’(X)ç < 1 и достаточное условие сходимости выполняется. Кроме того, эта производная > 1 на интервале [a, b] и характер сходимости будет монотонный.

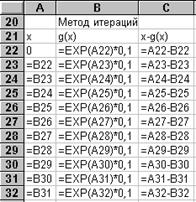
Запрограммируем метод итераций для этого примера на том же рабочем листе, где мы проводили отделение корней. В ячейку А22 внесем число, равное 0. В ячейку В22 запишем формулу =0, 1*EXP(A22), а в ячейку С22 формулу =А22- В22. Таким образом 22 строка содержит данные по первой итерации. Чтобы получить в строке 23 данные по второй итерации, скопируем содержимое ячейки В22 в ячейку А23, записав в А23 формулу =В22. Далее надо скопировать формулы ячеек В22 и С22 в ячейки В23 и С23. Для получения данных всех остальных итераций надо выделить ячейки А23, В23, С23 и скопировать их содержимое в блок А24: C32. После этого следует проанализировать изменение D = Х - g(X) в столбце С, найти D< 0, 00001 по модулю и выбрать соответствующее ему значение Х из столбца А. Это и есть приближенное значение корня.

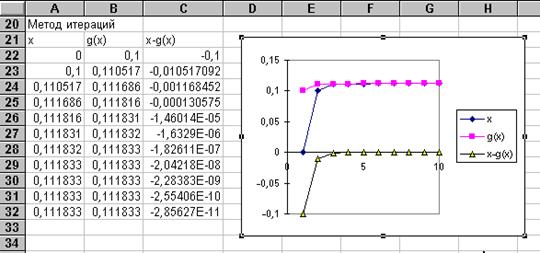
Для большей наглядности можно построить диаграмму для метода итераций. Выделяя блок А22: С32 и используя Мастер диаграмм, получим три графика изменения Х, g(X) и D в зависимости от номера итераций, для чего на шаге 3 из 5 выберем формат 2, а на шаге 4 из 5 построения диаграммы нужно отвести ноль столбцов для меток оси Х. Теперь хорошо виден монотонный характер сходимости D.

Для уточнения второго корня этого уравнения на интервале [3, 5; 4], нужно выбрать другую итерирующую функцию, такую чтобы ее первая производная была по модулю меньше единицы. Выберем g(X)= LN(X)+LN(10). В ячейку А22 внесем новое Х0=3, 75, а в ячейку В22 - новую формулу =LN(A22)+LN(10). Скопируем формулу из В22 в блок В23: В32 и сразу получим новые данные и перестроенную диаграмму. Определим приближенное значение второго корня.

1. 3 Уточнение корней: метод Ньютона.

Для уточнения корня методом Ньютона должно быть дано:

1) уравнение f(X) = 0, причем f(X) должно быть задано в виде формулы,

2) числа a - левая граница и b - правая граница интервала, внутри которого лежит один корень,

3) число Е - заданная точность получения корня,

4) функция f(X) должна быть дважды дифференцируемой, причем формулы f’(X) и f”(X) должны быть известны.

Метод состоит в итерационных вычислениях последовательности

X_i+1 = X_i - f(X_i)/f’(X_i), где i=0, 1, 2, ...,

исходя из начального приближения Х₀, принадлежащего интервалу [a, b] и удовлетворяющего условию f(X₀)*f”(X₀)> 0. Достаточные условия сходимости метода заключаются в том, что первая и вторая производные исследуемой функции должны сохранять знак на интервале [a, b]. В качестве начального приближения выбирают обычно или a, или b, в зависимости от того, кто из них соответствует формуле выбора Х₀.

Метод Ньютона допускает простую геометрическую интерпретацию. Если через точку с координатами (X_i; f(X_i)) провести касательную к кривой f(X), то абсцисса точки пересечения этой касательной с осью 0Х и есть очередное приближение корня Х_i+1.

Метод Ньютона можно рассматривать как некоторую модификацию метода итераций, дающую наилучшую итерирующую функцию g(X) на каждом шаге итерации. Проведем следующие преобразования с исходным каноническим уравнением f(X)=0. Умножим левую и правую его части на некоторое число l, отличное от нуля. Затем прибавим слева и справа по Х. Тогда будем иметь

Х = g(X) = Х +l*f(X).

Дифференцируя g(X), получим g’(X) = 1 + l*f’(X). Из достаточного условия сходимости метода итераций ç g’(X)ç < 1. Потребуем, чтобы на i-том шаге итерации сходимость была самой быстрой, т. е. ç g’(X_i)ç =0. Тогда l=-1/ f’(X_i) и мы пришли к методу Ньютона.

Вычислительная процедура метода состоит в следующем. Выбираем начальное приближение X₀, обычно равное a или b. Затем вычислим X₁= X₀ - f(X₀)/f’(X₀) и D= X₁- X₀. Если модуль D < = E, то X₁ является корнем уравнения. В противном случае переходим ко второй итерации: вычисляем Х₂и новое значение D=X₂- X₁. Опять проводим проверку на точность и при необходимости продолжаем итерации. Если X₀ выбрано правильно, а функция удовлетворяет достаточному условию сходимости, то эта итерирующая процедура быстро сойдется к корню.

Пример 1. 3.

Уточним методом Ньютона значение корня, отделенного в примере 1. 1. Итак пусть f(X)= exp(X) - 10*X, для первого корня a=0 и b=0, 5. Пусть Е=0, 00001. Формулы для первой и второй производной f(X) таковы

f’(X) = exp(X) - 10 и f”(X) = exp(X).

Очевидно, что X₀= a = 0, т. к. f(0)*f”(0) = 1 > 0.

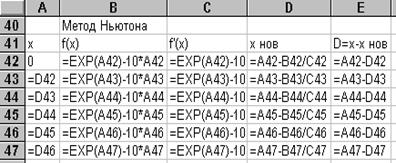
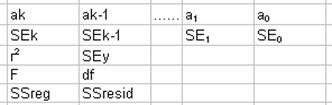
Запрограммируем метод Ньютона для этого примера на том же рабочем листе, где мы проводили отделение корней. В ячейку А42 внесем число, равное Х₀=0. В ячейку В42 запишем формулу =EXP(A42)-10*А42, в ячейку С42 формулу =EXP(A42)-10, а в ячейку D42 формулу =А42- В42/C42. Затем в ячейку Е42 запишем формулу =А42-D42. Таким образом 42 строка содержит данные по первой итерации.

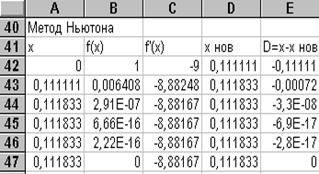
Чтобы получить в строке 43 данные по второй итерации, скопируем содержимое ячейки D42 в ячейку А43, записав в А43 формулу =D42. Далее надо скопировать формулы ячеек В42, С42, D42, E42 в ячейки В43, С43, D43, E43. Для получения данных всех остальных итераций надо выделить ячейки в 43 строке и скопировать их содержимое в блок А44: Е47. После этого следует проанализировать изменение D в столбце E, найти D< 0, 00001 по модулю и выбрать соответствующее ему значение Х из столбца А. Это и есть приближенное значение корня. При правильно введенных формулах метод Ньютона сходится за 3 или 4 итерации. Поэтому строить диаграмму для этого метода нет необходимости.

1. 4. Уточнение корней: метод бисекции ( деления отрезка пополам ).

Для уточнения корня методом бисекции должно быть дано:

1) уравнение f(X) = 0, причем f(X) должна быть задана в виде формулы,

2) числа a - левая граница и b - правая граница интервала, внутри которого лежит один корень,

3) число Е - заданная точность получения корня.

Напомним, что на концах интервала функция f(X) имеет разные знаки. Вычислительная процедура метода состоит в том, что на каждом шаге итерации на интервале [a, b] выбирают промежуточную точку с так, чтобы она являлясь серединой интервала, т. ет с=(a+b)/2. Тогда интервал разделится этой точкой на два равных отрезка [a, c] и [c, b], длины которых равны (b-a)/2. Из двух полученных отрезков выберем тот, на концах которого функция f(X) принимает значения противоположных знаков. Обозначим его снова как [a, b]. На этом заканчивается первая итерация. Далее новый отрезок [a, b] делим снова пополам и проводим вторую и последующие итерации. Процесс деления отрезка пополам производим до тех пор, пока на каком-либо К-том шаге вновь получающийся отрезок не станет меньше или равным величине точности Е. Значение шага К легко рассчитать из формулы

(b-a)/2^k < =E,

где a и b - начальные значения левой и правой границ интервала.

Метод бисекций сходится для любых непрерывных функций, в том числе и недифференцируемых.

Пример 1. 4.

Уточним методом бисекции значение корня, отделенного в примере 1. 1. Итак пусть f(X)= exp(X) - 10*X, для первого корня a=0 и b=0, 5. Пусть Е=0, 00001.

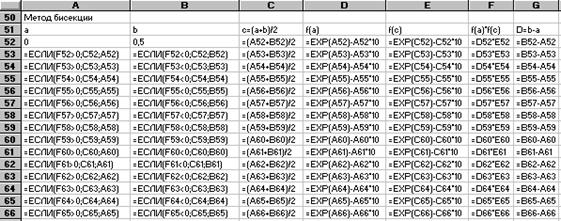
Запрограммируем метод бисекции для этого примера на том же рабочем листе, где мы проводили отделение корней. В ячейки А52 и В52 надо внести числовые значения a и b, в ячейку С52 - формулу =(А52+В52)/2. Далее в ячейку D52 внесем формулу =EXP(A52)-10*A52, в ячейку Е52 - формулу =EXP(C52)-10*C52, в ячейку F52 - формулу =D52*E52, и, наконец, в ячейку G52 запишем формулу =B52- A52. В строке 52 мы сформировали первую итерацию. На второй итерации значения в ячейках А53 и В53 зависят от знака числа в ячейке F52. Если F52> 0, то значение А53 равно С52. В противном случае оно должно быть равно А52. В ячейке В53 наоборот: если F52< 0, то значение В53 равно С52, иначе В52.

Разрешить это затруднение поможет встроенная функция EXCEL, которая носит название ЕСЛИ. Сделаем текущей ячейку А53. В строке формул, рядом с зеленой галочкой щелкнем на кнопке с изображением f(x). Так вызывается Мастер Функций. В появившемся диалоге выберем в поле Категории Функции категорию Логические, а в поле Имя Функции - имя ЕСЛИ. На втором шаге диалога заполним три свободных поля следующим образом: в поле Логическое_выражение внесем “F52> 0” (разумеется без кавычек! ), в поле Значение_если_истина внесем С52, а в поле Значение_если_ложь - А52. Щелкнем по кнопке Закончить. Вот и все.

То же самое надо проделать с ячейкой В53. Только Логическое выражение будет “F52< 0”, Значение_если_истина будет С52, а Значение_если_ложь соответственно В52.

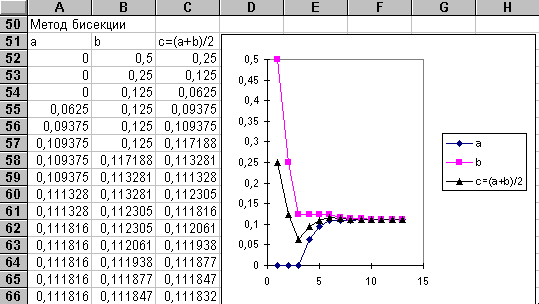
Далее надо скопировать формулы в блоке ячеек С52: G52 в блок С53: G53. После этого вторая итерация будет проведена в строке 53. Для получения следующих итераций достаточно скопировать формулы из строки 53 в блоке А53: E53 в блок А54: E68. Затем, как обычно, следует найти с столбце Е такую строку, где значение D будет меньше Е. Тогда число в столбце С в этой строке и есть приближенное значение корня.

Можно построить диаграмму изменения значений в столбцах А, В и С, начиная с первой и кончая последней итерацией. Для этого нужно выделить блок ячеек А52: С68. За дальнейшими инструкциями обратитесь к примеру 1. 2.

1. 5 Уточнение коней: подпрограмма EXCEL “Подбор параметра”.

EXCEL обладает большим набором средств, позволяющих решить те или иные вычислительные задачи. Для решения нелинейного уравнения предусмотрена подпрограмма Подбор параметра. Продемонстрируем действие этой подпрограммы на предыдущем примере.

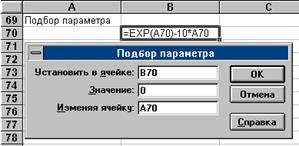
Уточним значение корня, отделенного в примере 1. 1. Итак пусть f(X)= exp(X) - 10*X. Найдем корень, лежащий на интервале [0; 0, 5]. Оставим пустой ячейку А70. В ячейку В70 запишем формулу =EXP(A70)-10*A70. Выберем команду меню Сервис- Подбор параметра. Откроется диалог Подбор параметра, в котором в поле Установить в ячейке запишем В70, в поле Значение занесем 0 (ноль), в поле Изменяя ячейку укажем А70. Щелкнем по кнопке ОК и появится новый диалог, в котором будет показан результат выполнения операции. В окне Состояние подбора решения будет показано найденное значение. Теперь если щелкнуть на кнопке ОК, в ячейку А70 будет внесено найденное значение корня, а в ячейку B70 - значение функции.

Для того, чтобы найти другой корень, лежащий на интервале [3, 5; 4] необходимо изменить начальное приближение, которое в нашей таблице находится в ячейке A70. Запишем в эту ячейку одну из границ интервала, например, 4, и снова выполним процедуру подбора параметра. Содержимое клеток A70 и B70 изменится, теперь в этих клетках появятся координаты большего корня.

2. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.

В общем виде система линейных алгебраических уравнений записывается так: a₁₁x₁+a₁₂x₂+... +a_1nx_n = b₁

a₂₁x₁+a₂₂x₂+... +a_2nx_n = b₂

....................................................

a_n1x_n+a_n2x₂+... +a_nnx_n = b_n

Совокупность коэффициентов этой системы запишем в виде квадратной матрицы A из n строк и n столбцов

a₁₁ a₁₂ ... a_1n

a₂₁ a₂₂... a_2n

...........................

a_n1 a_n2... a_nn

Используя матричное исчисление, исходную систему уравнений можно записать в виде

А*Х = В,

где Х - вектор- столбец неизвестных размерностью n, а В - вектор- столбец свободных членов, тоже размерностью n.

Эта система называется совместной, если она имеет хотя бы одно решение, и определенной, если она имеет одно единственное решение. Если все свободные члены равны нулю, то система носит название однородной.

Необходимым и достаточным условием существования единственного решения системы является условие DET=0, где DET - определитель матрицы А. На практике при вычислениях на компьютере не всегда удается получить точное равенство DET нулю. В том случае, когда DET близко к нулю, системы называются плохо обусловленными. При их решении на компьютере малые погрешности в исходных данных могут привести к существенным погрешностям в решении. Условие DET~0 является необходимым для плохой обусловленности системы, но не достаточным. Поэтому при решении системы на ЭВМ требуется оценка погрешности, связанной с ограниченностью разрядной сетки компьютера.

Существуют две величины, характеризующие степень отклонения полученного решения от точного. Пусть Хк - истинное решение системы, Хc - решение, полученное тем или иным методом на ЭВМ, тогда погрешность решения:
Е = Хк - Хc. Вторая величина - невязка, равная R = B - A*Xc. В практических расчетах контроль точности осуществляется с помощью невязки, хотя это и не совсем корректно.

2. 1. Матричный метод.

EXCEL дает возможность решить систему линейных алгебраических уравнений матричным методом, т. е.

Х = А-1*В.

Таким образом, алгоритм решения системы матричным методом можно представить в виде следующей последовательности вычислительных процедур:

1) получить матрицу А^-1, обратную матрицеА;

2) получить решение системы по формуле Хс = А^-1*В;

3) вычислить новый вектор свободных членов Вс = А*Хс;

4) вычислить невязку R = B - Bc;

5) получить решение системы по формулеdXc = А^-1*R;

6) сравнить все компоненты вектора dXc по модулю с заданной погрешностью Е: если все они меньше Е, то закончить вычисления, иначе повторить вычисления с п. 2, гдеХс = Xc + dXc.

Рассмотрим матричный метод решения системы с помощью EXCEL на примере.

Пример 2. 1.

Решить систему уравнений

20, 9x₁+ 1, 2x₂ + 2, 1x₃+ 0, 9x₄ = 21, 7

1, 2x₁+21, 2x₂ + 1, 5x₃+ 2, 5x₄ = 27, 46

2, 1x₁+ 1, 5x₂ +19, 8x₃+ 1, 3x₄ = 28, 76

0, 9x₁+ 2, 5x₂ + 1, 3x₃+32, 1x₄ = 49, 72

EXCEL имеет следующие встроенные функции, реализующие матричные вычисления:

а) МОБР - обращение матрицы,

б) МУМНОЖ - умножение двух матриц,

в) МОПРЕД - вычисление определителя матрицы.

При использовании этих функций важно правильно и компактно расположить на рабочем листе блоки ячеек, соответствующие исходным и рабочим матрицам и вектор-столбцам. Откроем новый рабочий лист, щелкнув на выбранном Вами ярлычке. Отведем под матрицу А блок ячеек А3: D6. Для наглядности заключим его в черную рамку. Для этого выделим блок A3: D6, дадим команду меню Формат- Ячейки и в открывшемся диалоге выберем вкладку Рамка. Откроется новый диалог, в котором щелкнем по полю Рамка- Контур и выберем в поле Рамка- Стиль самую толстую ширину линии. Подтвердим свое решение, щелкнув на кнопке ОК. Выделим теперь блок A8: D11 под матрицу А^-1 и также заключим его в черную рамку, проделав действия, аналогичные блоку матрицы А. Далее выделим блоки ячеек под вектор-столбцы (обведя их черной рамкой): блок F8: F11 - под векторВ, блок H8: H11 - под вектор Хс, получающийся в результате умножения А^-1*В, блок H3: H6 - под вектор Вс, получающийся в результате умноженияА*Хс, причем для наглядности выделим дополнительный блок F3: F6, куда скопируем компоненты вектора Хс из блока H8: H11. И наконец, занесем в ячейки Е4 и Е9 знак умножения *, а в ячейки G4 и G9 знак равенства =, затем, выделяя по очереди столбцы Е и G, дадим команду меню Формат- Столбец - Подгон ширины. Таким образом мы подготовили рабочий лист к решению нашей задачи.

Внесем исходные данные: числа матрицы А в ячейки блока A3: D6, а числа вектора свободных членовВ - в ячейки блока F8: F11.

Начнем выполнение алгоритма с обращения матрицы А. Для этого выделим блок А8: D11, куда должен быть помещен результат операции. Этот блок окрасится в черный цвет, за исключением ячейки А8. Щелкнем по кнопке f_x на панели Стандартная, осуществив вызов Мастера Функций. Откроется диалог, в котором из поля Категория функций выберем строку Мат. и тригонометрия, а из поля Имя функции - строку МОБР. Перейдем ко второму шагу диалога, щелкнув по кнопке Шаг> . Здесь в поле Массив надо набить с клавиатуры А3: D6, что соответствует блоку ячеек, занятому матрицей А. Щелкнув на кнопке Закончить, можно увидеть, что в блоке А8: D11 заполнена лишь ячейка А8. Для завершения операции обращения EXCEL требует выполнения еще двух действий. Сначала надо сделать активной строку формул, щелкнув по ней ( в любом месте строки! ) - курсор мыши примет при этом форму I. Проверкой правильности Ваших действий будет появление слева от строки формул четырех кнопок, в том числе с зеленой галочкой. После этого следует нажать на клавиатуре клавишу “Ctrl”, затем не отпуская ее - клавишу “Shift”, и не отпуская и ее - клавишу “Enter”, т. е. в результате должны быть нажаты все три клавиши одновременно! Вот теперь весь блок А8: D11 будет заполнен числами и можно выделить блок H8: H11, чтобы начать операцию умножения А^-1*В.

Выделив этот блок, снова вызовите Мастер функций и в поле Имя функции - выбирайте функцию МУМНОЖ. Щелкнув по кнопке Шаг> , перейдем ко второму шагу диалога, где в поле Массив1 внесем адрес А8: D11, а в поле Массив2 - адрес F8: F11. Щелкнем по кнопке Закончить и обнаружим, что в блоке Н8: H11 заполнена лишь ячейка Н8. Активизируем строку формул ( должна появиться зеленая галочка! ) и по методике, описанной выше, нажмем одновременно три клавиши “Ctrl”-”Shift”-”Enter”. Результат умножения появится в блоке Н8: H11.

Для проверки точности полученного решения системы, проведем операцию вычисленияВс=А*Хс. С этой целью скопируем только числовые значения ( а не формулы! ) ячеек из блока H8: H11 в ячейки F3: F6. Сделать это надо следующим образом. Выделим блок H8: H11. Дадим команду меню Правка- Копировать. Выделим блок F3: F6. Дадим команду меню Правка- Специальная вставка. Откроется диалог, в котором в поле Вставить следует выбрать режим Значения. Подтвердим свое решение, щелкнув по кнопке ОК.

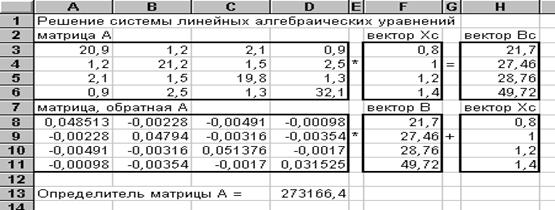
После этой операции заполнены числами блоки А3: D6 и F3: F6. Можно приступить к умножению матрицы А на вектор Хс. Для этого надо выделить блок Н3: H6, вызвать Мастер Функций и, действуя так же, как и при вычислении Хс=А^-1*В, получить Вс. Как видно из таблицы, числовые значения векторов В и Вс совпадают, что говорит о хорошей точности вычислений, т. е. невязка в нашем примере равна нулю.

Подтвердим хорошую обусловленность матрицы А вычислением ее определителя. Для этого сделаем активной ячейку D13. С помощью Мастера Функций вызовем функцию МОПРЕД. В поле массив занесем адрес блока А3: D6. Щелкнув по кнопке Закончить, получим в ячейке D13 числовое значение определителя матрицы А. Как видно, оно значительно больше нуля, что говорит о хорошей обусловленности матрицы.

2. 2. Метод приближенных вычислений.

Одним из наиболее распространенных итерационных методов решения систем линейных алгебраических уравнений, отличающийся простотой и легкостью программирования, является метод приближенных вычислений или метод Якоби.

Пусть надо решить систему

a₁₁x₁+a₁₂x₂+a₁₃x₃ = b₁

a₂₁x₁+a₂₂x₂+a₂₃x₃ = b₂

a₃₁x₁+a₃₂x₂+a₃₃x₃ = b₃

Предположим, что диагональные элементы a_11, a_22,a₃₃ отличны от нуля. В противном случае можно переставить уравнения. Выразим переменные из первого, второго и третьего уравнений соответственно. Тогда

x₁= [b₁-( a₁₂x₂+a₁₃x₃)]/ a₁₁

x₂= [b₂-( a₂₁x₁+a₂₃x₃)]/ a₂₂

x₃= [b₃-( a₃₁x₁+a₃₃x₃)]/ a₃₃

Зададим начальные приближения неизвестных

x₁= x₁⁽⁰⁾

x₂= x₂⁽⁰⁾

x₃= x₃⁽⁰⁾

Подставляя их в правую часть преобразованной системы, получим новое первое приближение

x₁⁽¹⁾ = [b₁-( a₁₂x₂⁽⁰⁾+a₁₃x₃⁽⁰⁾)]/ a₁₁

x₂⁽¹⁾= [b₂-( a₂₁x₁⁽⁰⁾+a₂₃x₃⁽⁰⁾)]/ a₂₂

x₃⁽¹⁾= [b₃-( a₃₁x₁⁽⁰⁾+a₃₃x₃⁽⁰⁾)]/ a₃₃

На этом заканчивается первая итерация. Далее, используя вычисленные значения x₁⁽¹⁾, x₂⁽¹⁾ и x₃⁽¹⁾, можно провести следующую итерацию, чтобы найти x₁⁽²⁾, x₂⁽²⁾ и x₃⁽²⁾, Итерационный процесс продолжается до тех пор, пока на какой-либо k-той итерации все значения x_i^(k) не станут близкими к x_i^(k-1). Близость этих значений можно характеризовать максимальной абсолютной величиной их разности D. Тогда при заданной допустимой погрешности Е критерий окончания итерационного процесса можно записать так

D = max [ABS(x_i^(k) - x_i^(k-1))] < =E для i=1, 2, 3.

Достаточные условия сходимости итерационного процесса

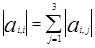где j#i, i=1, 2, 3

При этом хотя бы для одного уравнения неравенство должно выполняться строго.

Пример 2. 2.

Решим систему примера 2. 1 методом Якоби.

Дано:

система уравнений

20, 9x₁+ 1, 2x₂ + 2, 1x₃+ 0, 9x₄ = 21, 7

1, 2x₁+21, 2x₂ + 1, 5x₃+ 2, 5x₄ = 27, 46

2, 1x₁+ 1, 5x₂ +19, 8x₃+ 1, 3x₄ = 28, 76

0, 9x₁+ 2, 5x₂ + 1, 3x₃+32, 1x₄ = 49, 72

начальные приближения

x₁⁽⁰⁾= b₁=21, 7

x₂⁽⁰⁾= b₂=27, 46

x₃⁽⁰⁾= b₃=28, 76

x₄⁽⁰⁾= b₄=49, 72

допустимая погрешность

Е = 1Е –5.

Очевидно, что достаточные условия сходимости метода выполняются. Откроем новый рабочий лист EXCEL. Внеся в ячейку А1 текст с названием метода, отведем вторую строку для заголовка таблицы

Ячейка	Текст заголовка
А2	№ итерации
В2	Х1
С2	Х2
D2	X3
E2	X4
F2	DX1
G2	DX2
H2	DX3
I2	DX4
J2	D

Следующая третья строка должна содержать информацию о нулевой итерации, т. е. в ячейку А3 занесем ноль, а в ячейки В3, С3, D3 и E3 – начальные приближения, равные значениям свободных членов уравнения.

Четвертая строка будет содержать формулы для вычисления первой итерации

Ячейка	Формула
А4
В4	=(21, 7 – (1, 2C3+2. 1D3+0. 9*E3))/20. 9
С4	=(27. 46-(1. 2B3+1. 5D3+2. 5*E3))/21. 2
D4	=(28. 76-(2. 1B3+1. 5C3+1. 3*E3))/19. 8
E4	=(49. 72-(0. 9B3+2. 5C3+1. 3*D3))/32. 1
F4	=ABS(B4-B3)
G4	=ABS(C4-C3)
H4	=ABS(D4-D3)
I4	=ABS(E4-E3)
J4	=МАКС(F4: I4)

Для проведения остальных итераций следует скопировать формулы ячеек B4: J4 в нижние строки с 5 по, например, 15. Если числовые значения в столбце J будут меньше Е, решение найдено. В противном случае следует продолжить копирование. Результат решения показан на рисунке.

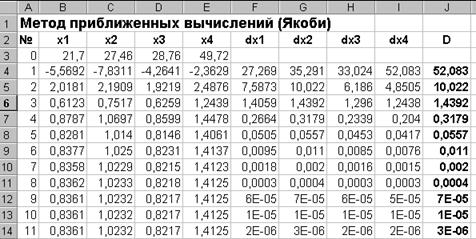
2. 3. Метод Гаусса – Зайделя.

Этот метод является модификацией метода приближенных вычислений и отличается от него формулами вычислений первого и последующего приближений.

Пусть надо решить систему

a₁₁x₁+a₁₂x₂+a₁₃x₃ = b₁

a₂₁x₁+a₂₂x₂+a₂₃x₃ = b₂

a₃₁x₁+a₃₂x₂+a₃₃x₃ = b₃

x₁= [b₁-( a₁₂x₂+a₁₃x₃)]/ a₁₁

x₂= [b₂-( a₂₁x₁+a₂₃x₃)]/ a₂₂

x₃= [b₃-( a₃₁x₁+a₃₃x₃)]/ a₃₃

Зададим начальные приближения неизвестных

x₁= x₁⁽⁰⁾

x₂= x₂⁽⁰⁾

x₃= x₃⁽⁰⁾

Подставляя их в правую часть преобразованной системы, получим новое первое приближение

x₁⁽¹⁾ = [b₁-( a₁₂x₂⁽⁰⁾+a₁₃x₃⁽⁰⁾)]/ a₁₁

x₂⁽¹⁾= [b₂-( a₂₁x₁⁽¹⁾+a₂₃x₃⁽⁰⁾)]/ a₂₂

x₃⁽¹⁾= [b₃-( a₃₁x₁⁽¹⁾+a₃₃x₃⁽¹⁾)]/ a₃₃

На этом заканчивается первая итерация. В отличии от метода Якоби, здесь использовались не только начальные приближения, но и уже вычисленные значения неизвестных на первой итерации. Далее, используя вычисленные значения x₁⁽¹⁾, x₂⁽¹⁾ и x₃⁽¹⁾, можно провести следующую итерацию, чтобы найти x₁⁽²⁾, x₂⁽²⁾ и x₃⁽²⁾, Итерационный процесс продолжается до тех пор, пока на какой-либо k-той итерации все значения x_i^(k) не станут близкими к x_i^(k-1). Близость этих значений можно характеризовать максимальной абсолютной величиной их разности D. Тогда при заданной допустимой погрешности Е критерий окончания итерационного процесса можно записать так

D = max [ABS(x_i^(k) - x_i^(k-1))] < =E для i=1, 2, 3.

Достаточные условия сходимости итерационного процесса

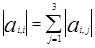где j#i, i=1, 2, 3

При этом хотя бы для одного уравнения неравенство должно выполняться строго.

Пример 2. 3.

Решим систему примера 2. 1 методом Гаусса-Зайделя. При этом оформление листа EXCEL останется тем же. Изменятся лишь формулы в четвертой и последующих строках.

Ячейка	Формула
А4
В4	=(21, 7 – (1, 2C3+2. 1D3+0. 9*E3))/20. 9
С4	=(27. 46-(1. 2B4+1. 5D3+2. 5*E3))/21. 2
D4	=(28. 76-(2. 1B4+1. 5C4+1. 3*E3))/19. 8
E4	=(49. 72-(0. 9B4+2. 5C4+1. 3*D4))/32. 1
F4	=ABS(B4-B3)
G4	=ABS(C4-C3)
H4	=ABS(D4-D3)
I4	=ABS(E4-E3)
J4	=МАКС(F4: I4)

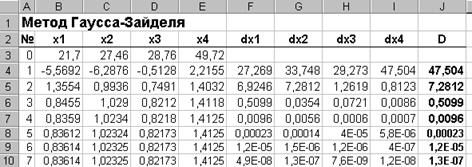
Как видно, в данном случае метод Гаусса – Зайделя оказался быстрее метода приближенных вычислений.

3. РЕШЕНИЕ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.

Система нелинейных уравнений в общем виде записывается так

f₁(x₁, x₂,... x_n) = 0

f₂(x₁, x₂,... x_n) = 0

..............................

f_n(x₁, x₂,... x_n) = 0

где f_i - нелинейные алгебраические функции. Для решения таких систем обычно используются итерационные методы. Ниже будут рассмотрены два метода - метод Ньютона и метод итераций. Успех применения этих методов во многом определяется выбором начальных приближений. Они должны быть достаточно близки к истинному значению. В противном случае итерационный процесс может не сойтись. Следует заметить, что в общем случае формализованных процедур выбора начальных приближений нет. Только в случае системы второго порядка можно предложить такую процедуру, сравнительно легко реализующуюся на EXCEL.

3. 1. Выбор начальных приближений.

Пусть задана система нелинейных уравнений 2-го порядка

f₁(x₁, x₂) = 0

f₂(x₁, x₂) = 0

Зададим несколько значений x₁ в диапазоне от х_нач до х_конс шагом dx. Подставим сначала в f₁(x₁, x₂) = 0 значение х_нач. Тогда это уравнение становится одномерным, зависящим только от х₂, и его можно решить подпрограммой EXCEL Подбор параметра (см. 2. 4). То же самое можно проделать и для всех остальных значений х₁. В результате мы будем иметь набор значений х₁ и х₂, для которых f₁(x₁, x₂) = 0. Далее, для того же самого набора значений х₁, используя подпрограмму Подбор параметра, найдем значения х₂, для которых f₂(x₁, x₂) = 0. Если теперь построить с помощью EXCEL графики изменения х₂ в зависимости от х₁ для двух этих случаев, то на пересечении этих графиков можно приближенно определить значения начальных приближений по х₁ и х₂. Если графики не пересекаются, следует задать новый диапазон изменения х₁ и повторить процедуру сначала.

Пример 3. 1.

Пусть надо решить систему

х₁³ + х₂³ - 6х₁ + 3 = 0

х₁³ - х₂³ - 6х₂ + 2 = 0

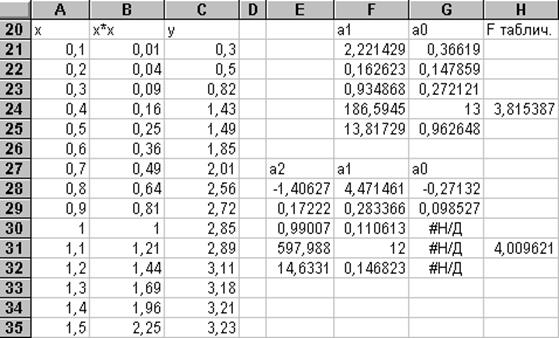
Подберем начальные приближения. Выберем х_нач = 0, х_кон = 1, dx = 0, 2. Откроем новый рабочий лист EXCEL и занесем эти значения х₁ в блок А4: A9. Выделим блок В4: В9 под значения х₂ первой серии, для которой f₁(x₁, x₂) = 0, и блок С4: С9 - под значения х₂ второй серии, для которой f₂(x₁, x₂) = 0. Блок D4: D9 отведем для функции f₁(x₁, x₂), а блок Е4: Е9 - для функции f₂(x₁, x₂). Сделаем текущей ячейку D4. В нее запишем формулу =А4^3+B4^3-6*A4+3. В ячейку Е4 запишем формулу =A4^3-C4^3-6*C4+2. Теперь выделим блок D4: E4 и скопируем эти формулы в блок ячеек D5: E9. Разумеется, адреса ячеек столбцов А и С в них будут автоматически изменены.

Перейдем к заполнению блока В4: В9. Снова сделаем текущей ячейку D4. Дадим команду меню Сервис- Подбор параметра. В открывшемся диалоге в поле Установить в ячейке должен быть указан адрес ячейки D4 в абсолютных адресах. В поле Значение следует занести ноль, а в поле Изменяя ячейку - занести адрес ячейки В4 ( можно в относительных адресах). Щелкнем по кнопке ОК. Появится новый диалог Состояние подбора параметра. Если решение найдено, то, щелкнув по кнопке ОК, получим в ячейке B4 нужное нам числовое значение. Далее эту процедуру надо повторить для всех ячеек блока D4: D9. В результате будет заполнен блок В4: В9.

Аналогичным образом следует заполнить блок С4: С9, используя блок Е4: Е9.

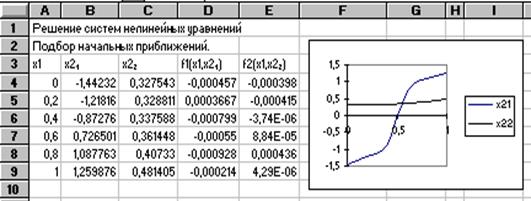
Если блоки в столбцах В и С заполнены, можно построить диаграмму. Для этого необходимо выделить блок А3: Е9. Затем щелкнуть по кнопке Мастер Диаграмм на панели Стандартная. Передвигаясь по диалогу с помощью кнопки Шаг> , выполнить все 5 шагов построения диаграммы, причем на Шаге 2 из 5 выбрать тип XY-точечная, а на Шаге 3 из 5 - формат 6. Анализируя построенную диаграмму, можно сделать вывод о том, что в качестве начальных приближений можно выбрать х1 =0, 5 и х2 = 0, 5.

3. 2 Метод Ньютона.

Пусть задана система нелинейных уравнений 2-го порядка

f₁(x₁, x₂) = 0

f₂(x₁, x₂) = 0

причем левые части уравнений известны в виде формул. Заданы также числовые значения начальных приближений х₁₀ и х₂₀, а также Е - точность вычислений значений корней. Функции должны быть дифференцируемы и формулы частных производных тоже должны быть известны.

Исходную систему можно записать в матричном виде

F(X) = 0,

где X - двумерный вектор- столбец с компонентами { x₁, x₂ }, а F - двумерный вектор- функция. Метод Ньютона - это метод последовательных приближений по формуле

Х_i+1 = X_i - P_i,

где P_i = J_i^-1*F_i,

i - номер итерации, ( i = 0, 1, 2,... )

J_i^-1 - матрица, обратная матрице J на i-той итерации,

J- матрица Якоби, т. е. матрица первых частных производных:

df₁/dx₁df₁/dx₂

df₂/dx₁df₂/dx₂.

Таким образом на каждой итерации вычисляется вектор Р, его компоненты сравниваются с заданной погрешностью Е по формуле

D=( p_1i²+p_2i²)^(1/2),

причем когда D < = E, вычисления прекращаются и вектор Х_i считается решением. В противном случае вычисляются новые значения Х и выполняется следующая итерация.

Достаточным условием сходимости метода служит неособенность матрицы Якоби, т. е. ее определитель (якобиан) не должен быть равным нулю на любой итерации.

Пример 3. 2.

Решим систему из примера 3. 1 методом Ньютона. Начальные приближения также возьмем из того же примера. Пусть Е = 0, 00001. Выпишем формулы частных производных:

df₁/dx₁ = 3x₁² - 6 df₁/dx₂ = 3x₂²

df₂/dx₁ = 3x₁²df₂/dx₂ = -3x₂² - 6.

Для решения задачи воспользуемся встроенными в EXCEL матричными функциями и процедурами так, как это сделано в разделе 2 настоящего пособия при решении систем линейных уравнений.

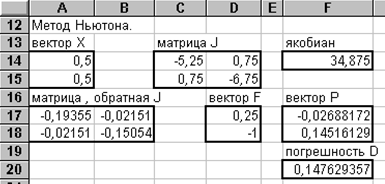
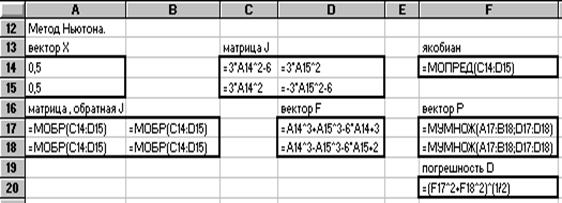
Проведем вычисления на том же рабочем листе, что и в примере 3. 1. Необходимо отвести блоки ячеек для векторов Х, F и P, для матриц J иJ^-1, а также ячейки для вычисления якобиана и текущей величины погрешности D. Затем занести начальные приближения в блок Х и формулы в блокиJ иF. Далее с помощью Мастера функций надо организовать вычисление якобиана функцией МОПРЕД, матрицы J^-1 - функцией МОБР и вектора Р - функцией МУМНОЖ по аналогии с примером 2. 1. В результате будет выполнена первая итерация метода Ньютона и по численному значению D следует принять решение о проведении дальнейших итераций.

Из таблицы ясно, что D> E и дальнейшие итерации необходимы. По формуле Ньютона для получения новых числовых значений вектора Х нужно из значений блока Хвычесть значения блока Р. Это можно выполнить таким образом. Выделим блок Ри дадим команду меню Правка- Копировать. Затем выделим блок Хи дадим команду меню Правка- Специальная вставка. В появившемся диалоге выберем в поле Вставить переключатель Значения, а в поле Операция - переключатель Вычесть и подтвердим свой выбор щелчком по кнопке ОК. В результате будет выполнена вторая итерация. Блок ячеек Р будет обрамлен бегущей пунктирной линией. Если значение D получится все еще большим чем Е, то следует снова выделить блок Х и повторить команду меню Правка- Специальная вставка с указанием тех же переключателей. Эти манипуляции можно проводить до тех пор, пока D не станет меньше, чем Е. Во время проведения итераций нужно визуально контролировать числовое значение якобиана для выполнения достаточных условий сходимости метода.

3. 3. Метод итераций.

Пусть задана система нелинейных уравнений 2-го порядка

f₁(x₁, x₂) = 0

f₂(x₁, x₂) = 0

причем левые части уравнений известны в виде формул. Заданы также числовые значения начальных приближений х₁₀ и х₂₀, а также Е - точность вычислений значений корней.

Для применения итераций исходная система приводится к виду

х₁ = g₁(x₁, x₂)

x₂ = g₂(x₁, x₂),

где функции g_i называются итерирующими. Алгоритм решения задается итерирующими формулами

х_1i+1 = g₁(x_1i, x_2i)

x_2i+1 = g₂(x_1i, x_2i),

где i -номер итерации, i = 0, 1, 2,... Для прекращения итераций вычисляются значения

p_1i+1 = х_1i+1 - x_1i

p_2i+1 = x_2i+1 - x_2i,

D=( p_1i²+p_2i²)^(1/2),

и D сравнивается с Е. Итерации продолжаются до тех пор, пока не выполнится условие D< =E. Чтобы процесс вычислений сходился к этому условию, нужно выполнениедостаточного условия сходимости:

ç dg₁/dx₁ç + ç dg₁/dx₂ç < 1,

ç dg₂/dx₁ç + ç dg₂/dx₂ç < 1.

Возможно также суммирование по столбцам.

Пример 3. 3.

Решим систему из примера 3. 1 методом итераций. Начальные приближения также возьмем из того же примера. Пусть Е = 0, 00001. Выпишем формулы для итерирующих функций

g₁(x₁, x₂) = (x₁³+ x₂³ + 3)/6

g₂(x₁, x₂) = (x₁³ - x₂³ + 2)/6.

При изменении независимых переменных в пределах 0< = x₁< =1 и 0< = x₂< =1 достаточное условие сходимости выполняется, т. к.

ç dg₁/dx₁ç + ç dg₁/dx₂ç = (x₁²)/2 + (x₂²)/2,

ç dg₂/dx₁ç + ç dg₂/dx₂ç = (x₁²)/2 + ç -(x₂²)/2ç.

Проведем вычисления на том же рабочем листе, что и в примере 4. 2.

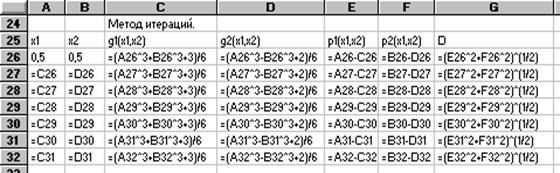
Отведем столбец А, начиная с 26 строки под значения х₁, столбец В под значения х₂, столбец С - под g₁, столбец D - под g₂, следующие три столбца под р₁, р₂ и D.

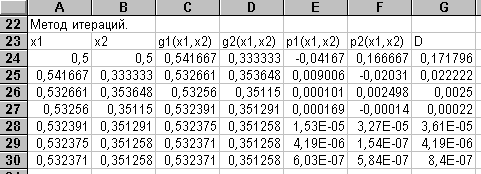
В строке 27 сформируем формулы для второй итерации, а затем скопируем их в блок А28: G32, с учетом изменений относительных адресов ячеек. В результате будем иметь заполненную таблицу

Как видно, процесс итераций сходится достаточно быстро.

4. ЧИСЛЕННЫЕ МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ.

Одномерная задача оптимизации в общем случае формулируется следующим образом: найти значение независимой переменной Х, заданной на интервале[a, b], при котором некоторая целевая функция f(X) принимает минимальное значение. Если ставится задача нахождения максимума, например, функции g(X), то преобразованием f(X) = - g(X) она приводится к отысканию минимума f(X). Целевая функция f(X) должна быть задана в виде формулы. Если существует производная f’(X), то задача сводится к решению уравнения f’(X) = 0, например, методами, описанными в разделе 2.

Численные методы оптимизации используются тогда, когда целевая функция недифференцируема и, в общем случае, может быть не гладкой и даже непрерывной, т. е. может иметь разрывы первого рода по Дирихле.

Единственное условие, предъявляемое к целевой функции - она должна быть унимодальной на интервале [a, b], т. е. иметь на этом интервале только один минимум и не иметь ни максимумов, ни точек перегиба. Математически свойство унимодальности записывается так. Функция f(X) называется унимодальной на интервале [a, b], если на этом интервале существует такая точка Х*, что для значений Х

X₁< X₂< X*< X₃< X₄

выполняется условие

f(X₁)> f(X₂)> f(X*)< f(X₃)< f(X₄).

В этом определении очень важно, что все неравенства - строгие.

Процесс нахождения минимума унимодальной функции численными методами оптимизации, называемыми иногда методами поиска, состоит в последовательном сужении интервала [a, b] - начального интервала неопределенности - так, чтобы его длина достигала значения Е - заданной погрешности решения.

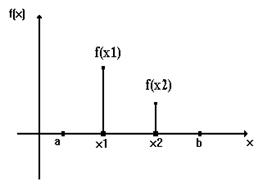
Алгоритм сужения интервала [a, b] называется стратегией поиска. Заметим, что если выбрать два любых значения Х₁ и Х₂ на интервале [a, b] и вычислить для них значения функции f(X₁) и f(X₂), то сравнивая эти значения по величине и используя свойство унимодальности, всегда можно сократить начальный интервал неопределенности, отбрасывая отрезок [a, X₁] или отрезок [X₂, b]. Таким образом, стратегии поиска отличаются правилами выбора значений Х₁ и Х₂ на интервале [a, b]. Далее будут рассмотрены три метода одномерной оптимизации.

4. 1. Метод дихотомии.

Для использования метода дихотомии должно быть дано:

а) формула целевой функции f(X),

б) численные значения а - левой границы и b - правой границы начального интервала неопределенности, на котором целевая функция унимодальна,

в) численное значение Е - точности нахождения значения Х, при котором f(X) принимает минимальное значение на [a, b].

Сущность метода состоит в том, что выбираются значения Х₁ и Х₂ так, чтобы они были как можно ближе к середине интервала неопределенности с=(a+b)/2. Обычно Х₁ = с-r и Х₂ = c+r, где r = E/3 или E/4 в зависимости от точности вычислений компьютера. Таким образом, на каждой итерации отбрасывается отрезок длиной (c-r), почти равной половине интервала неопределенности. Через К итераций начальный интервал неопределенности уменьшится до длины

d = (b-a)/2^K + r(2^K- 1)/2^(K-1).

Итерации прекращаются, если d < = E.

Итак, алгоритм метода дихотомии состоит в следующем.

1) для заданных значений a и b вычисляются с=(a+b)/2, X₁ = c-E/3 и X₂=c+E/3,

2) вычисляются значения f(X₁) и f(X₂) и сравниваются между собой,

3) если f(X₁) > f(X₂), то а= X₁, иначе b= X₂,

4) если длина нового интервала d=(b-a) < =E, то вычисления останавливаются и в качестве решения можно взять любое значение Х, лежащее внутри этого интервала; в противном случае выполняется новая итерация.

Пример 4. 1.

Пусть надо найти минимум функции f(X) = 2X² + e^-X. По правилам EXCEL эта функция должна быть записана так =2*Х^2 + EXP(-X), где вместо Х нужно подставить тот или иной адрес ячейки. Зададим Е= 0, 0001.

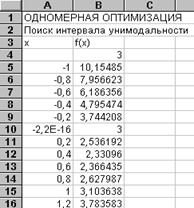
Первый этап решения задачи состоит в нахождении начального интервала неопределенности, на котором функция f(X) унимодальна. С помощью EXCEL это легко сделать, протабулировав функцию f(X) в некоторых пределах, например, от -1 до 1 с шагом 0, 2.

Откроем новый рабочий лист EXCEL. Поместим числовой ряд Х в блок А5: А16, оставив ячейку А4 пустой. В ячейку В4 занесем формулу =2*А4^2+EXP(-А4). Далее можно воспользоваться подпрограммой ТАБЛИЦА, вызвав ее командой меню Данные- Таблица и действуя так, как описано в примере 2. 1. Как видно из таблицы, интервал неопределенности можно выбрать между а=0 и b=1.

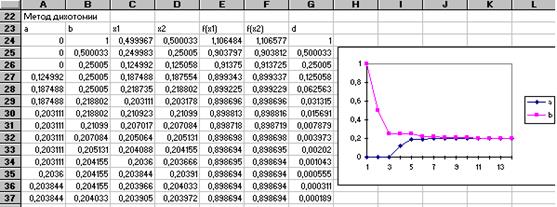
Запрограммируем решение нашей задачи методом дихотомии в блоке А24: G37, внеся необходимые числовые значения и формулы. Для изменения значений a и b используем функцию ЕСЛИ Мастера Функций. Приведем таблицу формул в соответствующих ячейках для первых двух итераций в строках 24 и 25. Формулы для остальных строк блока копируются из 25 строки.

Адрес	Формула
A24
B24
C24	=(A24+B24)/2-0, 0001/3
D24	=(A24+B24)/2+0, 0001/3
E24	=2*C24^2+EXP(-C24)
F24	=2*D24^2+EXP(-D24)
G24	=B24-A24
A25	=ЕСЛИ(E24> F24; C24; A24)
B25	=ЕСЛИ(E24< F24; D24; B24)
C25	=(A25+B25)/2-0, 0001/3
D25	=(A25+B25)/2+0, 0001/3
E25	=2*C25^2+EXP(-C25)
F25	=2*D25^2+EXP(-D25)
G25	=B25-A25

Из вычислений видно, что достаточно 12 итераций для получения решения с заданной точностью. Для построения диаграммы, иллюстрирующей изменения концов интервала неопределенности, следует выделить блок А23: В37 и воспользоваться Мастером Диаграмм, выбрав тип График и формат 1.

4. 2. Метод золотого сечения.

Как известно, золотым сечением отрезка называют деление отрезка так, что отношение длины всего отрезка к длине большей части равно отношению длины большей части к меньшей части отрезка. Нетрудно проверить, что золотое сечение отрезка [a, b] производят две симметричные точки

Х₁ = a + L(b-a) и X₂ = b - L(b-a), где L = (3 - Ö (5))/2.

Заметим, что точка Х₁в свою очередь производит золотое сечение отрезка
[a, X₂], а точка X₂ - золотое сечение отрезка [Х₁, b].

Опишем алгоритм поиска. Начальный отрезок [a, b] делим точками Х₁и X₂ по правилу золотого сечения. Вычисляем значения функций f(Х₁) и f(X₂). Сравнение этих значений позволяет отбросить либо интервал [a, Х₁], либо интервал [X₂, b]. На оставшемся интервале уже есть одна точка, производящая его золотое сечение. Поэтому следует вычислить значение второй такой точки. На этом заканчивается первая итерация. Таким образом на каждой итерации, начиная со второй, требуется лишь одно вычисление функции и при этом интервал неопределенности уменьшается на величину L ~ 0, 382. Итерации продолжаются до тех пор, пока интервал неопределенности [a, b] не станет меньше заданной точности решения Е.

Пример 4. 2.

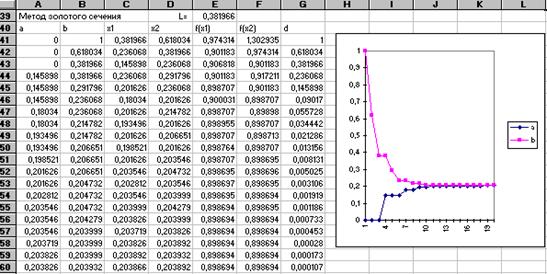
Решим задачу примера 4. 1 методом золотого сечения на том же рабочем листе, на котором приведено решение методом дихотомии. Величину L вычислим в ячейке Е39, а под решение отведем блок А41: G60. Приведем таблицу формул в соответствующих ячейках для первых двух итераций в строках 41 и 42. Формулы для остальных строк блока копируются из 42 строки. Для вычисления квадратного корня из 5 используется функция КОРЕНЬ Мастера Функций. В формулах строк 41 и 42 использован абсолютный адрес ячейки Е39, т. к. он не должен меняться при копировании.

Адрес	Формула
E39	(3-КОРЕНЬ(5))/2
A41
B41
C41	=A41+(B41-A41)*$E$39
D41	=B41-(B41-A41)*$E$39
E41	=2*C41^2+EXP(-C41)

F41	=2*D41^2+EXP(-D41)
G41	=B41-A41
A42	=ЕСЛИ(E41> F41; C41; A41)
B42	=ЕСЛИ(E41< F41; D41; B41)
C42	=ЕСЛИ(E41> F41; D41; A42+(B42-A42)*$E$39
D42	=ЕСЛИ(E41< F41; C41; B42-(B42-A42)*$E$39)
E42	=2*C42^2+EXP(-C42)
F42	=2*D42^2+EXP(-D42)
G42	=B41-A41

Как видно из таблицы, и в этом случае широко используется функция ЕСЛИ Мастера функций. После того как блок будет заполнен формулами, EXCEL предоставит решение задачи. Данный метод сходится медленнее метода дихотомии и количество итераций для получения решения с одинаковой точностью методом золотого сечения будет большей. Как и в предыдущем примере, можно построить диаграмму изменения концов интервала неопределенности.

4. 3. Встроенная подпрограмма EXCEL “Поиск решения”.

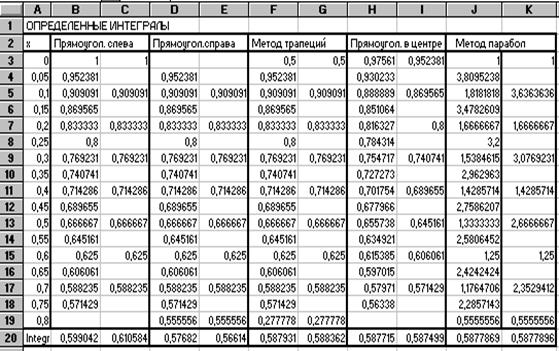
EXCEL имеет специальную подпрограмму, позволяющую решать многие оптимизационные задачи, в том числе и задачи одномерной оптимизации. Продемонстрируем применение этой подпрограммы для решения задачи из примера 4. 1. Будем искать решение на том же рабочем листе. Выделим ячейку А63 для значений независимой переменной Х, а ячейку В63 - для значений целевой функции f(X). Занесем в ячейку В63 формулу =2*А63^2 + EXP(-A63).

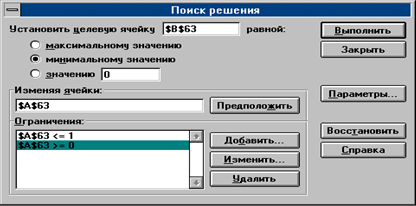
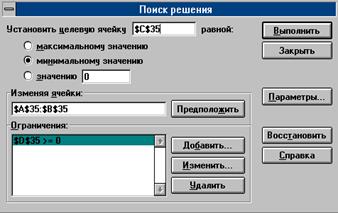
Теперь можно запустить подпрограмму, дав команду меню Сервис- Поиск решения. Откроется диалог Поиск решения. В поле Установить целевую ячейку занесем адрес В63, с помощью переключателей в левой части диалога установим режим поиска минимального значения в этой ячейки. В поле Изменяя ячейки занесем адрес А63 и, наконец, в списке Ограничения укажем дополнительные условия нахождения минимума c помощью кнопки Добавить. Для нашей задачи таких условий два: А63³ 0 и A63£ 1. Они указывают начальный интервал неопределенности, на котором целевая функция унимодальна.

Поиск решения начинается щелчком на кнопке Выполнить. Когда программа находит решение, открывается новый диалог Результаты поиска решений. Щелчком на кнопке ОК можно сохранить найденное решение.

5. МНОГОМЕРНЫЕ ЗАДАЧИ ОПТИМИЗАЦИИ.

В этом разделе будут рассмотрены методы, позволяющие находить минимум целевой функции многих переменных u = f(X₁, X₂, ... , Xn). Из курса математического анализа известно, что значения независимых переменных, при которых целевая функция достигает минимума, можно найти, решая систему нелинейных уравнений

du/dX₁= 0,

du/dX₂ = 0,

....................

du/dXn = 0.

Рассмотренный прием можно использовать лишь для дифференцируемой целевой функции, но и в этом случае могут возникнуть серьезные вычислительные трудности (см. раздел 3).

Здесь мы рассмотрим численные методы оптимизации, основанные на идее целенаправленного поиска минимума. Эти методы различаются прежде всего по характеру изменения целевой функции: если нет никаких ограничений ни на изменение независимых переменных, ни на значения целевой функции, то это - методы безусловной оптимизации. При наличии каких-либо ограничений используются методы условной оптимизации.

Кроме того, методы многомерной оптимизации классифицируются по возможности использования частных производных от целевой функции: если производные не используются, то это - методы прямого поиска, в противном случае - градиентные методы.

5. 1. Безусловная оптимизация: метод покоординатного спуска.

Это метод прямого поиска, в котором используются только значения целевой функции. Чтобы воспользоваться этим методом, необходимо иметь следующие исходные данные:

а) формулу целевой функции f(X₁, X₂, ... , Xn),

б) Е - точность нахождения значений независимых переменных, при которых функция достигает минимума,

в) начальные приближения X₁₀, X₂₀... , Xn₀.

Зафиксируем все значения Х-ов в виде начальных приближений, кроме первого. Тогда f(X₁, X₂₀... , Xn₀) - функция одной переменной X₁. Решая задачу одномерной оптимизации, найдем минимум этой функции по координате X₁ при фиксированных остальных координатах - X₁₁. В этом состоит первый шаг процесса оптимизации, заключающийся в спуске по координате X₁.

Зафиксируем теперь все координаты, кроме X₂. Снова решая одномерную задачу оптимизации, находим минимум функции по координате X₂. Далее процедура повторяется до Xn. На этом заканчивается первая итерация.

Таким образом, метод покоординатного спуска сводит многомерную задачу оптимизации к многократному решению одномерных задач по каждой независимой пременной.

После каждой итерации вычисляется

D = ç Х_1i+1 - X_1iç + ç Х_2i+1 - X_2iç +.... +ç Хn_i+1 - Xn_iç

и если D< =E, то вычисления прекращаются и последний набор Х-ов считается решением. В противном случае проводится следующая итерация.

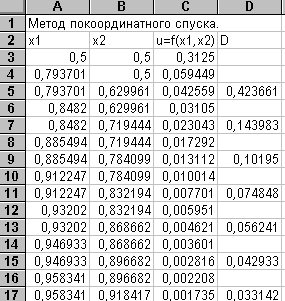
Пример 5. 1.

Число независимых переменных равняется двум. Ограничения отсутствуют. Требуется найти минимум функции

u = (X₂-X₁²)²+ (1-X₁)²

из начальной точки ( 0, 5; 0, 5) c точностью 0, 0001. Проанализировав функцию, заметим, что она будет иметь минимум, равный нулю. Для чего и первое, и второе слагаемое тоже должны быть равны нулю. Откуда координаты точки минимума (1; 1).

Решим эту задачу на EXCEL. Откроем новый рабочий лист. Выделим столбец А под значения X₁, столбец В - под значения X₂, в столбец С будем заносить значения целевой функции и, наконец, в столбец D - значения погрешности D.

Занесем в ячейки А3 и В3 значения начальных приближений, равных 0, 5 и в ячейку С3 формулу =(В3-А3^2)^2+(1-A3)^2. Скопируем эту формулу в блок ячеек С4: С17. На этом заканчивается подготовительный этап.

1 итерация.

1 шаг. Скопируем содержимое ячейки В3 в ячейку В4. Сделаем текущей ячейку С4. Процесс одномерной оптимизации для нахождения X₁выполним с помощью подпрограммы EXCEL Поиск решения. Вызовем эту подпрограмму командой меню Сервис- Поиск решения. В открывшемся диалоге в поле Установить целевую ячейку занесем адрес С4, а в поле Изменяя ячейки - адрес А4. Щелкнем по кнопке Выполнить и, во вновь открывшемся диалоге Результаты поиска решения щелкнем по кнопке ОК. В результате в ячейке А4 получим числовое значение, при котором целевая функция достигает минимального значения в ячейке С4 по координате X₁.

2 шаг. Скопируем содержимое ячейки А4 в ячейку А5. Сделаем текущей ячейку С5. Дадим команду меню Сервис- Поиск решения. В открывшемся диалоге в поле Установить целевую ячейку занесем адрес С5, а в поле Изменяя ячейки - адрес В5. Щелкнем по кнопке Выполнить и, во вновь открывшемся диалоге Результаты поиска решения щелкнем по кнопке ОК. В результате в ячейке В5 получим числовое значение, при котором целевая функция достигает минимального значения в ячейке С5 по координате X₂.

3 шаг. Занесем в ячейку D5 формулу =ABS(A3-A5)+ABS(B3-B5) для вычисления погрешности решения на первом шаге. На этом заканчивается первая итерация.

Вторая и все последующие итерации проводятся аналогично, но с учетом соответствующих адресов ячеек. Например, во второй итерации будут участвовать адреса ячеек в 6 и 7 строках. Результаты проведения первых семи итераций представлены в таблице. Как видно, значения целевой функции уменьшаются от шага к шагу, но метод сходится чрезвычайно медленно.

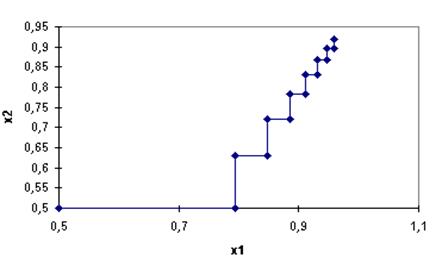
Можно построить диаграмму изменения на каждой итерации, выделив блок А2: В17 с помощью Мастера Диаграмм, выбрав тип диаграммы XY-точечная и формат 2. На диаграмме хорошо видны перпендикулярные ломаные линии движения от точки к точке параллельно одной из осей координат.

5. 2. Безусловная оптимизация: метод наискорейшего спуска.

Это метод градиентного поиска, в котором используются как значения целевой функции, так и значения ее первых частных производных. Чтобы воспользоваться этим методом, необходимо иметь следующие исходные данные:

а) формулу целевой функции f(X₁, X₂, ... , Xn),

б) Е - точность нахождения значений независимых переменных, при которых функция достигает минимума,

в) начальные приближения X₁₀, X₂₀... , Xn₀,

г) формулы первых частных производных целевой функции по каждой независимой переменной.

С помощью рассмотренного ранее метода покоординатного спуска осуществляется поиск в направлении, параллельном одной из осей координат, до точки минимума в этом направлении. Кажется разумным попытаться модифицировать этот метод таким образом, чтобы на каждом шаге поиск минимума производился вдоль “наилучшего” направления. Не ясно, какое направление является наилучшим, но известно, что направление градиента является направлением наискорейшего возрастания функции. Следовательно, противоположное направление - антиградиента - является направлением наискорейшего убывания функции.

Множество точек, для которых целевая функция имеет постоянное значение, называется линией уровня. Направление градиента перпендикулярно к любой точке линии уровня. Под градиентом понимается вектор-столбец из первых частных производных целевой функции, если она непрерывна и дифференцируема.

Идея метода наискорейшего спуска состоит в следующем. Выбираем начальную точку и вычисляем в ней градиент целевой функции. Определяем направление поиска, противоположное градиенту. Решая задачу одномерной оптимизации, ищем точку минимума целевой функции по этому направлению.

Например, для функции двух переменных формулы первой итерации будут иметь вид

u = f(X_1нов, X_2нов) Þ min,

где X_1нов = X₁₀- h(du/dX₁)_X10 и X_2нов = X₂₀-h(du/dX₂)_X20, а h - длина отрезка от точки нулевого приближения до точки минимума по выбранному направлению. Эта длина определяется методом одномерной оптимизации. На этом кончается первая итерация.

В найденной точке (X_1нов, X_2нов) снова вычисляем градиент, снова определяем направление поиска, снова методом одномерной оптимизации ищем точку минимума. Эти итерации продолжаются до тех пор, пока не выполнится условие прекращения вычислений, а именно: квадратный корень из суммы квадратов частных производных целевой функции должен быть меньше заданной точности Е.

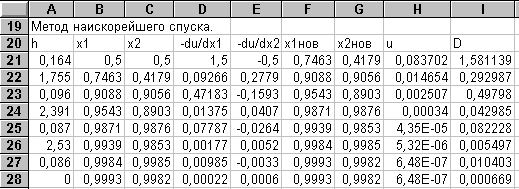
Пример 5. 2.

Решим задачу примера 5. 1 методом наискорейшего спуска. Для этого прежде всего найдем частные производные целевой функции

u = (X₂-X₁²)²+ (1-X₁)²,

du/dX₁= - 4(X₂-X₁²) X₁-2(1-X₁),

du/dX₂= 2(X₂-X₁²).

Составляющие антиградиента должны быть взяты с обратным знаком

antigrad u = {- du/dX₁, -du/d X₂}.

Будем решать задачу на том же рабочем листе, где мы исследовали метод покоординатного спуска. Выделим столбец А под переменную h, столбцы В и С - под X₁, X₂, столбцы D и Е - под составляющие антиградиента, столбцы F и G - под X_1нов, X_2нов, столбец Н - под целевую функцию u, столбец I - под переменную D. Приведем таблицу формул в соответствующих ячейках для первых двух итераций в строках 21 и 22. Заметим, что числовые значения в столбце А появляются в результате выполнения подпрограммы EXCEL Поиск решения для решения задачи одномерной оптимизации. Формулы блока В23: I28 получаются путем копирования в них формул блока В22: I22.

ячейка	формула
B21	0, 5
C21	0, 5
D21	=4(C21-B21^2)B21+2*(1-B21)
E21	=-2*(C21-B21^2)
F21	=B21+A21*D21
G21	=C21+A21*E21
H21	=(G21-F21^2)^2+(1-F21)^2
I21	=КОРЕНЬ(D21^2+E21^2)
B22	=F21
C22	=G21
D22	=4(C22-B22^2)B22+2*(1-B22)
E22	=-2*(C22-B22^2)
F22	=B22+A22*D22
G22	=C22+A22*E22
H22	=(G22-F22^2)^2+(1-F22)^2

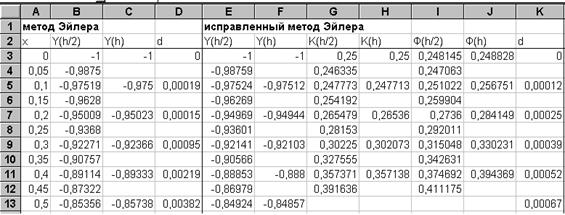
После подготовки формул в блоке А21: I28, проведем первую итерацию. Для этого сделаем текущей ячейку Н21. Дадим команду меню Сервис- Поиск решения. В появившемся диалоге занесем в поле Установить целевую ячейку адрес Н21, а в поле Изменяя ячейки - адрес А21. Щелкнув по кнопке Выполнить, получим новый диалог, в котором щелкнем по кнопке ОК. В результате в ячейке А21 получим значение h, а ячейках F21 и В22 - новое значение Х1, в ячейках G21 и С22 - новое значение Х2.

Теперь можно приступить ко второй итерации, сделав текущей ячейку Н22. Снова используя подпрограмму Поиск решения так же, как и в первой итерации, получим очередные новые значения шага и независимых переменных. Продолжая итерации, как видно из таблицы, можно получить решение с заданной точностью за семь итераций. Точность решения контролируется по столбцу I.

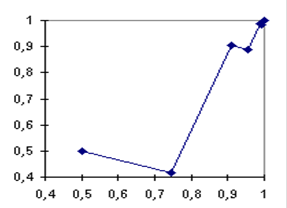
Выделяя блок В20: С28, можно построить диаграмму, аналогично примеру 5. 1. На ней изображены перпендикулярные ломаные линии, причем в отличие от примера 5. 1 их направление не совпадает с направлениями координатных осей.

5. 3. Безусловная оптимизация: подпрограмма EXCEL “Поиск решения”.

Подпрограмма Поиск решения позволяет решать не только задачи одномерной, но и многомерной оптимизации. В ней можно воспользоваться двумя более мощными методами: методом сопряженных градиентов и методом Ньютона. Оба метода - градиентные. Отличие их от метода наискорейшего спуска заключается в том, что составляющие антиградиента в них - частные производные целевой функции- вычисляются не аналитически, а методами численного дифференцирования.

Продемонстрируем применение этой подпрограммы для решения задачи примера 5. 1 на том же рабочем листе. Выделим ячейки А31 и В31 под независимые переменные Х₁ и Х₂, а ячейку С31 - под целевую функцию u.

Занесем в ячейку С31 формулу =(В31- A31^2)^2+(1-A31)^2. Cделав ячейку С31 текущей, вызовем подпрограмму командой меню Сервис- Поиск решения. В появившемся диалоге занесем в поле Установить целевую ячейку адрес С31, а в поле Изменяя ячейки - адреса A31: B31.

Теперь надо щелкнуть по кнопке Параметры. Откроется диалог Параметры поиска решения, в котором можно выбрать переключатели поля Оценка - квадратичная, поля Производные - прямые, поля Метод - сопряженных градиентов.

Щелкнув по кнопке Выполнить, получим новый диалог, в котором щелкнем по кнопке ОК. В результате в ячейке А31 получим минимальное значение Х₁, а в ячейке В31 - минимальное значение Х₂. Легко убедиться, что оба они очень близки к 1.

При желании можно повторить вычисления, выбрав другие значения переключателей и сравнив результаты вычислений.

5. 4. Условная оптимизация: метод штрафных функций.

Чтобы воспользоваться этим методом, необходимо иметь следующие исходные данные:

а) формулу целевой функции f(X₁, X₂, ... , Xn),

б) Е - точность нахождения значений независимых переменных, при которых функция достигает минимума,

в) начальные приближения X₁₀, X₂₀... , Xn₀,

г) формулы функций - ограничений в виде равенств g(X₁, X₂, ... , Xn)=0,

д) формулы функций - ограничений типа неравенств h(X₁, X₂, ... , Xn)> =0.

Здесь важно, что ограничения записаны в канонической форме, т. е. они или равны, или больше или равны нулю.

Сущность метода состоит в том, что задачу условной оптимизации при наличии ограничений мы заменяем на задачу безусловной оптимизации: поиска минимума некоторой другой - расширенной целевой функции без каких-либо ограничений

R(X₁, X₂, ... , Xn)= f (X₁, X₂, ... , Xn)+ Bs(X₁, X₂, ... , Xn),

где s - штрафная функция, В - коэффициент штрафа.

Штрафная функция должна учитывать заданные ограничения, а именно:

1) она должна равняться нулю для всех значений Х-ов, удовлетворяющих заданным ограничениям, т. е. когда все Х лежат в разрешенной области,

2) она должна быть очень большой, стремиться к бесконечности для тех точек, которые лежат в запрещенной области там, где ограничения не выполняются.

Таким образом, при выполнении ограничений в разрешенной области функции f (X₁, X₂, ... , Xn) и R(X₁, X₂, ... , Xn) имеют один и тот же минимум. Если хотя бы одно из ограничений нарушится, значение штрафной функции сильно возрастает и значение функции R(X₁, X₂, ... , Xn) значительно удаляется от минимума функции f(X₁, X₂, ... , Xn). Другими словами, при несоблюдении ограничений на целевую функцию налагается “штраф”.

Пусть есть только по одному ограничению типа равенства и неравенства. Тогда шрафную функцию можно записать в виде

s(X₁, X₂, ... , Xn)= g²(X₁, X₂, ... , Xn)+ h²(X₁, X₂, ... , Xn){1 - sign[h(X₁, X₂, ... , Xn)]},

где sign[Z] -знаковая функция, равная 1 при Z> 0 и равная -1 при Z< 0.

Если ограничение типа равенства выполняется, то g = 0, в противном случае первое слагаемое штрафной функции g²(X₁, X₂, ... , Xn) больше нуля и при умножении на коэффициент штрафа сильно увеличивает значение расширенной целевой функции.

Если ограничение типа неравенства выполняется, то h(X₁, X₂, ... , Xn) больше нуля, т. е. знаковая функция равна 1 и выражение в фигурных скобках равно нулю. В противном случае это выражение равно2, а значит второе слагаемое штрафной функции больше нуля и при умножении на коэффициент штрафа сильно увеличивает значение расширенной целевой функции. Таким образом, эта формула обеспечивает выполнение условий, наложенных на штрафную функцию. Если ограничений любого вида несколько, то для каждого из низ записываются аналогичные формулы и все они суммируются.

Доказано, что если минимум f лежит внутри разрешенной области, то минимумы R и f совпадают. В противном случае минимум R лежит снаружи вблизи границ разрешенной области. Поэтому этот метод называют иногда методом внешних штрафных функций.

Наибольшую трудность при применении этого метода вызывает выбор значения коэффициента штрафа В, который, по существу, определяет “вес” штрафной функции по сравнению с исходной целевой функцией. Нельзя сразу задать величину В очень большой, например, В=1000000, т. к. в этом случае “вес” штрафной функции намного превышает “вес” целевой функции и компьютер найдет минимум не функции f, а функции s. Поэтому используется следующий итерационный алгоритм.

Положим В=1. Из точки начального приближения методом покоординатного спуска ( или любым другим прямым методом поиска, т. к. знаковая функция не дифференцируема) начнем искать минимум расширенной целевой функции. Когда на каком-либо шаге покоординатного спуска модуль штрафной функции уменьшится приблизительно на порядок, увеличим величину коэффициента штрафа В на два порядка и продолжим поиск минимума расширенной целевой функции. Этот прием следует использовать до тех пор, пока модуль штрафной функции не станет меньше заданной точности Е.

Формальной проверкой правильности решения может служить близость полученных значений Х-ов к границе допустимой области ограничений, причем с внешней стороны.

Пример 5. 3.

Решим задачу примера 5. 1 методом штрафных функций. Как известно, координаты точки минимума есть (1; 1). Введем ограничение типа неравенства (Х₁²+Х₂²)< = 0, 64. Это означает, что решение может находиться лишь внутри окружности с центром в начале координат и радиусом, равным 0, 8. Таким образом, настоящий минимум лежит в запрещенной области и решение должно быть близко к окружности, определяемой ограничением, причем с внешней стороны.

Прежде всего перепишем формулу неравенства в каноническом виде

0, 64 -(Х₁²+Х₂²) > = 0.

Вернемся к рабочему листу EXCEL, на котором проведено решение примера 5. 1 методом покоординатного спуска. Там столбцы А и В отведены под независимые переменные, столбец С - под функцию f, столбец D - под значения погрешности D. Проведем подготовительный этап для метода штрафных функций. Для этого выделим блок А5: D17 и уничтожим его содержимое, нажав на клавиатуре клавишу “Delete”. В ячейку D3 занесем формулу = 0, 64-(A3^2+B3^2), в ячейку Е3 - формулу =D3^2*(1- ЗНАК(D3)), где функция ЗНАК соответствует знаковой функции sign. Если теперь в ячейку F3 занести 1, то в ячейке G3 можно сформировать формулу расширенной целевой функции =C3+F3*G3. На этом подготовительный этап заканчивается.

1 итерация. Скопируем формулы блока С3: G3 в блок С4: G30. Следует заметить, что заранее неизвестно, сколько итераций потребуется для получения решения. Поэтому может случиться, что формулы из 3 строки придется скопировать и ниже 30 строки. Сделаем ячейку А4 пустой, а в ячейку В4 занесем 0, 5. Теперь определим ячейку G4 текущей и проведем первый шаг метода покоординатного спуска так, как это описано в примере 6. 1. Продолжим шаги метода покоординатного спуска до тех пор, пока модуль чисел в столбце Е не уменьшится на порядок по сравнению с числом в ячейке Е3.

2 итерация. Изменим значение величины коэффициента штрафа, занеся число 100 в соответствующую ячейку столбца F, и вновь продолжим покоординатный спуск до тех пор, пока модуль чисел в столбце Е снова не уменьшится еще на порядок.

После этого следует опять увеличить В на два порядка и так до тех пор, пока какое-нибудь число в строке Е не станет меньше по модулю заданного значения Е. Числа в соответствующей строке в столбцах А и В и есть координаты точки минимума.

5. 5. Условная оптимизация: подпрограмма EXCEL “Поиск решения”.

Подпрограмма Поиск решения имеет модификацию методов сопряженных градиентов и Ньютона для решения задач условной оптимизации. Следует отметить, что эта модификация работает успешно лишь для некоторых видов целевой функции - линейной и квадратичной и лишь для некоторых видов ограничений, например, типа шара, координатного параллелепипеда, гиперплоскости или полиэдра. После вызова подпрограммы командой меню Сервис- Поиск решения появляется диалог, в котором кроме уже знакомых Вам полей Установить целевую ячейку и Изменяя ячейки, следует обратить внимание на поле Ограничения и кнопки управления ограничениями Добавить, Изменить и Удалить. Например, чтобы задать новое ограничение следует щелкнуть по кнопке Добавить. В открывшемся новом диалоге Добавить ограничение нужно внести адрес одной или блока ячеек в поле Ссылка на ячейку, а затем указать тип ограничения и его условия. После этого нужно щелкнуть по кнопке ОК. Работа с другими кнопками управления не вызывает затруднений.

Выбор параметров подпрограммы вызывается щелчком по кнопке Параметры. Работа с открывшемся диалогом описана в п. 5. 3.

Продемонстрируем работу подпрограммы решением задачи примера 5. 4.

Выделим ячейку А35 под переменную Х₁, ячейку В35 - под Х₂, в ячейку С35 запишем формулу целевой функции в обозначениях EXCEL

=(B35-A35^2)^2+(1- A35)^2, в ячейку D35 запишем формулу ограничений

=0, 68 - (A35^2+B35^2). Сделаем ячейку С35 текущей и дадим команду меню Сервис- Поиск решения. В открывшемся диалоге в поле Установить целевую ячейку занесем адрес С35, в поле Изменяя ячейки - адрес блока А35: В35. Теперь щелкнем по кнопке Добавить и в открывшемся новом диалоге в поле Ссылка на ячейку занесем адрес D35, выберем вид ограничения > = и правую часть ограничения - 0 (ноль). Щелкнув по кнопке ОК, вернемся к первоначальному диалогу.

Далее щелкнем по кнопке Параметры и выберем следующие переключатели: оценка - квадратичная, производные - прямые, метод - сопряженных градиентов. Щелкнув по кнопке Выполнить получим новый диалог Результаты поиска решения, в котором щелкнем по кнопке ОК. Результаты расчетов представлены в таблице. Особый интерес вызывает числовое значение в ячейке D35. Оно очень близко к нулю, но все же отрицательно, т. е. независимые переменные находятся в запрещенной области.

5. 6. Условная оптимизация: линейное программирование.

В общем случае задача линейного программирования формулируется следующим образом: найти величины X₁, …, X_n, при которых достигается экстремум (максимум или минимум) линейной целевой функции

u = a₁X₁ + a₂X₂ + … + a_nX_n

и удовлетворяется система ограничений вида

c_i1X₁+ … + c_in X_n < = b_i,

c_k1X₁+ … + c_kn X_n = b_k,

c_p1X₁+ … + c_pn X_n > = b_p, где i # k # p.

На практике часто встречаются условия неотрицательности всех или части переменных

X_j > = 0, j = 1, 2, …, s,

которые выделяют в особую группу.

Для решения задачи линейного программирования разработан специальный метод, названный симплекс – методом. Этот метод реализован в EXCEL в подпрограмме Поиск решения. В случае правильного решения задачи EXCEL печатает сообщение “Решение найдено. Все ограничения и условия оптимальности выполнены”. Если коэффициенты системы ограничений таковы, что эта система несовместна, то появится сообщение “Поиск не может найти подходящего решения”. Если же система ограничений такова, что область допустимых решений не ограничена сверху при поиске максимума ( или снизу при поиске минимума), то будет напечатано “Значения целевой ячейки не сходятся”.

Задача линейного программирования является достаточно распространенной задачей условной оптимизации, особенно в экономике. Решение этой задачи рассмотрим на примере задачи распределения ресурсов.

Пример 5. 4.

Пусть некоторое предприятие может изготавливать изделия 4 типов. Для изготовления изделий требуются ресурсы 3 видов: трудовые ресурсы, сырье и финансы. Количество ресурса каждого вида, необходимое для выпуска одной единицы изделия каждого типа, называется нормой расхода. Пусть все нормы расхода известны и приведены в таблице

ресурсы	изделие1	изделие2	изделие3	изделие4
трудовые
сырье
финансы

Пусть известна также прибыль, получаемая от реализации каждого типа изделия

	изделие1	изделие2	изделие3	изделие4
прибыль

и располагаемое количество ресурсов

ресурсы	наличие
трудовые
сырье
финансы

Необходимо найти такие количества изделий каждого типа, чтобы прибыль предприятия была максимальной.

Введем некоторые обозначения.

Пусть

а_j - прибыль, получаемая от реализации единицы изделия j-го типа,

b_i - располагаемое количество i-го ресурса,

с_ij - норма расхода i-го ресурса для изготовления единицы j-го изделия,

xj - неизвестное количество изделий j-го типа.

Целевую функцию - суммарную величину прибыли предприятия - можно записать так

u = а₁x₁+а₂x₂+а₃x₃+а₄x₄ Þ max.

Зная нормы расхода и располагаемое количество каждого ресурса, можно составить систему ограничений:

c₁₁x₁+c₁₂x₂+c₁₃x₃+c₁₄x₄ < = b₁

c₂₁x₁+c₂₂x₂+c₂₃x₃+c₂₄x₄ < = b₂

c₃₁x₁+c₃₂x₂+c₃₃x₃+c₃₄x₄< = b₃

Следует добавить также граничные условия из содержания задачи

x₁> =0, x₂> =0, x₃> =0, x₄> =0.

Для нашего примера

критерий оптимизации (целевая функция):

u = 60 x₁+70 x₂+120 x₃+130 x₄ Þ max

ограничения

x₁+ x₂+ x₃+ x₄< =16

6 x₁+5 x₂+4 x₃+3 x₄< =110

4 x₁+6 x₂+10 x₃+13 x₄< =100

граничные условия

x₁> =0, x₂> =0, x₃> =0, x₄> =0.

Откроем новый рабочий лист и подготовим его к решению задачи. Внесем исходные данные так, как это показано на рисунке.

Теперь надо подготовить таблицы, связанные с решением задачи, ячейки для целевой функции и ограничений

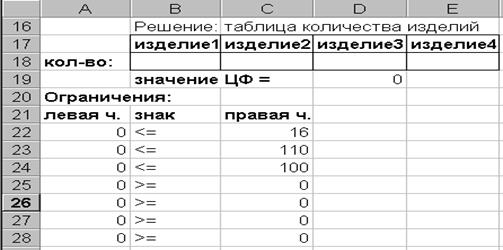
Далее внесем необходимые формулы для расчета:

ячейка	формула
D19	=CУММПРОИЗВ(В18: Е18; В10: Е10)
A22	=CУММПРОИЗВ(В18: Е18; В5: Е5)
A23	=CУММПРОИЗВ(В18: Е18; В6: Е6)
A24	=CУММПРОИЗВ(В18: Е18; В7: Е7)
A25	=B18
A26	=C18
A27	=D18
A28	=E18

После этого вызовем подпрограмму Сервис - Поиск решения. В появившемся диалоге внесем в окно Установить целевую ячейку адрес D19, в окно Изменяя ячейки адреса блока В18: Е18. Если в окне Ограничения оставлены какие-либо формулы от решения предыдущей задачи, их следует удалить по одному, выделяя каждое мышью и нажимая мышью кнопку Удалить. Затем следует внести нужные нам ограничения по одному, нажимая мышью кнопку Добавить. Каждый раз будет появляться новое диалоговое окно. Для первого ограничения в окно Ссылка на ячейку следует внести адрес А22, знак ограничения выбрать мышью из ниспадающего списка, а в правое окно занести адрес С22. Затем щелкнуть по кнопке Добавить и продолжить внесение ограничений.. Закончив ввод ограничений, щелкнем по кнопке ОКи снова попадем в окно Поиск решения.

Теперь щелкнем по кнопке Параметры. В открывшемся диалоге надо включить параметр Линейная модель. Щелкнув по кнопке ОК, возвратимся в окно Поиск решения.

Проверим, что переключатель указывает на поиск максимального значения и щелкнем по кнопке Выполнить. Появится новое диалоговое окно Результаты поиска решения. Если все формулы и ограничения были внесены правильно, то в этом окне будет написано “Решение найдено, Все ограничения и условия оптимальности выполнены”. Щелкнем по кнопке ОК и перейдем к анализу решения. Если же появится надпись “Поиск не может найти подходящего решения”, то щелкнем по кнопке Отмена и проверим правильность внесения исходных данных.

Результаты решения задачи нашего примера приведены в таблице

	изделие1	изделие2	изделие3	изделие4
кол-во

Значение целевой функции = 1320.

Анализ задачи линейного программирования на устойчивость и по пределам, который обычно проводят после получения решения, выходит за рамки данного пособия.

6. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ.

Пусть требуется исследовать зависимость Y=f(X), причем величины X и Y получены экспериментально, в одних и тех же экспериментах. Обычно считают, что величины Х измеряются точно, в то время как измерение величин Y содержит случайные ошибки. Это означает, что погрешность измерения Х пренебрежимо мала по сравнению с погрешностью измерения Y. Задача состоит в установлении функциональной зависимости Y = f(X) по результатам измерений (Xi, Yi), где i = 1, 2,..., n.

Пусть функция f(X) может быть представлена в виде f(X, a₁, a₂,..., a_k), где a₁, a₂,..., a_k - неизвестные параметры. Тогда результаты измерений можно представить как

Y_i = f(X_i, a₁, a₂,..., a_k)+c_i,

где c_i - случайные величины, характеризующие погрешности эксперимента. Обычно предполагают, что они - независимые нормально распределенные с нулевым математическим ожиданием и одинаковыми дисперсиями.

Задача состоит в том, чтобы по опытным данным наилучшим образом определить значения параметров a_k. При этом в методе наименьших квадратов считается, что наилучшими будут те значения параметров a_k, при которых сумма квадратов отклонений расчетных величин Y от экспериментальных окажется наименьшей, т. е.

S = S_i (f(X_i, a₁, a₂,..., a_k)- Y_i)² Þ min.

На практике метод наименьших квадратов состоит из трех этапов.

1 этап. Выдвигают гипотезу о виде функции f(X_i, a₁, a₂,..., a_k). Она должна быть линейна относительно параметров. Например, функция

a₀+a₁X_i+a₂X_i²+.... + a_k X_i^k

линейна по параметрам a_k, т. к. любая функция, на которую умножается любой параметр, полностью вычисляется по экспериментальным данным и не зависит от параметров.

2 этап. По имеющимся экспериментальным данным определяют численные оценки параметров. Для отыскания минимума функции S нужно приравнять нулю ее частные производные по параметрам

dS/da₀= 0

dS/da₁= 0

..............

dS/da_k = 0

Если f(X_i, a₁, a₂,..., a_k) линейна по параметрам, то полученная в результате дифференцирования система уравнений является системой линейных алгебраических уравнений. Решая ее методами, описанными, например, в разделе 3, можно получить значения параметров.

3 этап. Проверяют выдвинутую на первом этапе гипотезу о виде функции f, т. е. насколько эта функция адекватно описывает связь экспериментальных данных (Xi, Yi). Для этого вычисляют величину

F = ss/ss_resid,

где ss - общая сумма квадратов, равная сумме квадратов разностей между экспериментальными значениями Y_i и средним значением Y, посчитанным по всем экспериментам, ss_resid - остаточная сумма квадратов, равная S_i(f(X_i, a₁, a₂,..., a_k)- Y_i)². Вычисленное значение F сравнивают с F_табл, полученным по статистическим таблицам для критерия Фишера. Если F> F_табл, то считается что вид функции был выбран правильно, т. е. математическая модель описания эксперимента адекватна.

Иногда для проверки адекватности модели используют коэффициент детерминированности r², который изменяется в пределах от 0 до1. Если он равен 1, то выбранная модель абсолютно адекватна экспериментальным данным; если он равен 0, то никакой связи между экспериментом и выбранной моделью нет. Обычно по степени близости r²к 1 судят о мере адекватности математической модели.

Пример 6. 1.

Аппроксимировать полиномами первой и второй степени по методу наименьших квадратов экспериментальные данные, заданные таблицей:

EXCEL позволяет решить эту задачу несколькими способами. Рассмотрим вначале самый простой. Откроем новый рабочий лист и поместим заданные числовые данные в блок А3: В17, отведя столбец А под значения Х, а столбец В - под значения Y. Выделим блок А2: В17 и с помощью Мастера Диаграмм постоим график зависимости Y от Х, выбрав тип диаграммы - XY-точечная, формат 1. Щелкнув по кнопке Закончить на шаге 5 из 5, получим на рабочем листе диаграмму в виде 16 точек на плоскости X-Y. Поле диаграммы будет обведено черной рамкой. Поместим курсор мыши в виде стрелки внутрь поля диаграммы и дважды быстро щелкнем. Поле диаграммы станет активным, что подтверждается изменением рамки диаграммы - она будет заштрихована синей линией. Теперь надо расположить острие стрелки курсора на любую из 16 точек диаграммы и щелкнуть. Изменится цвет всех 16 точек. Дадим команду меню Вставка- Линия тренда. Откроется диалог Линия тренда. Выберем тип тренда - линейный, щелкнув на соответствующем квадратике. В этом же диалоге выберем вкладку Параметры. Сделаем активными два указателя - Показывать уравнение на диаграмме и Показывать значение R-квадрат на диаграмме. И, наконец, щелкнув по кнопке ОК, получим решение на диаграмме. Как видно, на ней не только появляется непрерывная прямая, соответствующая линейной функциональной зависимости, но и формула зависимости Y(X) с числовыми коэффициентами и значение коэффициента детерминированности.

Для аппроксимации исходных данных полиномом второго порядка нужно вновь дать команду меню Вставка-Линия тренда. В открывшемся диалоге выберем тип тренда - полиномиальный, в поле Степень - занесем число 2. Щелкнув по кнопке ОК, получим новую диаграмму с новыми формулами.

К сожалению, этот способ решения задачи дает слишком мало статистической информации и не позволяет статистически оценить адекватность модели.

Пример 6. 2.

Решим задачу примера 6. 1 с помощью встроенной в EXCEL функции ЛИНЕЙН. Для решения задачи нам понадобится столбец с числовыми значениями Х². Поэтому скопируем значения блока А2: А17 в блок А20: А35. В ячейку В20 занесем текст Х*Х, в ячейку В21 формулу = А21*А21 и скопируем ее в блок В22: В35. Наконец, в блок С20: С35 скопируем содержимое блока В2: В17. Таким образом, мы подготовили таблицу из 3 столбцов, в первом из которых содержатся числовые значения Х, во втором - Х², в третьем - Y.

Функция ЛИНЕЙН имеет 4 параметра, записываемых в скобках и разделяемых точкой с запятой

=ЛИНЕЙН( Р1; Р2; Р3; Р4),

где Р1 - адреса блока Y ( заметьте, пожалуйста, Y, а не Х! ),

Р2 - адреса блока Х,

Р3 - если вместо Р3 записано ИСТИНА, то а₀ вычисляется; если записано ЛОЖЬ - то а₀= 0;

Р4 - если вместо Р4 записано ИСТИНА, то вычисляются всевозможные статистические параметры, если записано ЛОЖЬ - то вычисляются только коэффициенты а_к,..., а₀. Статистические параметры помещаются в таблицу вида

В этой таблице а_к,..., а₀- коэффициенты математической модели,

SEk, ..., SE₀ - значения стандартных ошибок коэффициентов математической модели,

r² - значение коэффициента детерминированности 0 < r² < 1,

SEy - значение стандартной ошибки Y,

F - расчетное значение F-критерия.

df - cтепени свободы,

SSreg - регрессионная сумма квадратов, равная разности между общей суммой квадратов и остаточной суммой квадратов,

SSresid- остаточная сумма квадратов.

Проведем сначала расчет линейной модели. Занесем ячейку F20 текст: а₁, а в ячейку G20 - текст: а₀.

В ячейку F21 введем формулу

= ЛИНЕЙН(C21: C35; A21: A35; ИСТИНА; ИСТИНА)

и выделим блок F21: G25 под итоговую статистическую таблицу. Этот блок при выделении будет покрашен в черный цвет, за исключением ячейки F21. Cделаем строку формул этой ячейки активной, при этом рядом со строкой формул появится зеленая галочка. Теперь последовательно будем нажимать клавиши клавиатуры: “Ctrl”, затем, не отпуская ее, клавишу “Shift”, затем, не отпуская уже обе, клавишу “Enter”. В результате получим заполненную таблицу статистических коэффициентов в блоке F21: G25. Обратим внимание на содержимое ячеек F23 - там хранится коэффициент детерминированности и F24 - она содержит расчетное значение F-критерия.

Проверим адекватность рассчитанной модели. Для этого надо получить табличное значение F- критерия. Воспользуемся для этого статистической функцией EXCEL, которая называется FРАСПОБР. Сделаем текущей ячейку Н24. Вызовем Мастер функций и из группы Статистические выберем FРАСПОБР. Щелкнув по кнопке Шаг> , обратимся к диалогу, в котором в поле Вероятность занесем 0, 01, в поле Степени свободы 1 - занесем число 15 ( общее число заданных экспериментов), в поле Степени свободы 2 - число 13 ( это-df из статистической таблицы результатов, полученных для нашей модели). Если теперь щелкнуть по кнопке Закончить, то в ячейке Н24 получим F_табл. Поскольку оно много меньше числа в ячейке F24, то модель следует считать адекватной.

Перейдем к расчету квадратичной модели. Занесем в ячейки E27, F27, G27 тексты соответственно: а₂, а₁, а₀.

В ячейку Е28 введем формулу

= ЛИНЕЙН(C21: C35; A21: В35; ИСТИНА; ИСТИНА)

и выделим блок Е28: G32 под итоговую статистическую таблицу. Этот блок при выделении будет покрашен в черный цвет, за исключением ячейки Е28. Далее проделаем те же манипуляции, что и при расчете линейной модели. В результате получим статистическую таблицу.

Может вызвать недоумение содержание ячеек G30: G32. В них записано #Н/Д. Тем не менее, так и предусмотрено в EXCEL при правильной работе функции ЛИНЕЙН.

Выделим ячейку Н31 для расчета F_табл. При вызове функции FРАСПОБР изменится только число Степеней свободы 2. Оно в соответствии с полученной статистической таблицей равняется 12. Сравнив F c F_табл, увидим, что и оно гораздо больше F_табл. Поэтому и квадратичная модель статистически адекватна.

7. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ.

Формулы для приближенного вычисления определенных интегралов, называемые также квадратурными формулами, применяются очень часто. Дело в том, что для большого числа элементарных функций первообразные уже не выражаются через элементарные функции, в результате чего нельзя вычислить определенный интеграл по формуле Ньютона - Лейбница.

Для численного вычисления определенного интеграла должно быть задано:

1) формула f(X) -подынтегральной функции,

2) численные значения а- нижнего и b- верхнего пределов интегрирования,

3) численное значение Е - точности вычисления интеграла.

Общий подход к решению задачи будет следующим. Определенный интеграл I представляет собой площадь криволинейной трапеции, ограниченной кривой f(X), осью Х и прямыми х=а и х=b. Мы будем вычислять I, разбивая интервал от а до b на множество меньших интервалов, находя приблизительно площадь каждой малой полоски и суммируя площади этих полосок.

Разобьем интервал интегрирования на n равных частей, каждая длиной h=(b-a)/n. При этом интервал от а до b будет содержать (n+1) узлов х0, x1, ..., xn. Аппроксимируя f(X) на каждом малом интервале простейшими полиномами малого порядка, можно получить различные формулы вычисления интеграла I.

Заменяя f(X) прямыми, параллельными оси Х, получим различные формулы прямоугольников. Вычисляя Y_i =f(X_i) во всех узлах и учитывая, что площадь прямоугольника равна произведению основания, которое у всех элементарных интервалов одинаковое и равно h, на высоту, которое есть Y_i, получаем

для метода прямоугольников с узлом слева

Iслева ~ h*(Y₀+Y₁+Y₂+... +Y_n-1),

для метода прямоугольников с узлом справа

Iсправа ~ h*( Y₁+Y₂+... +Y_n-1+Y_n),

для метода прямоугольников с узлом в центре

Iцентр ~ h*[f(X₀+h/2), f(X₁+h/2), ..... , f(X_n-1+h/2)].

Если на каждом элементарном интервале заменить f(X) на трапецию, то

для метода трапеций

Iтрапеций ~ h*( Y₀/2+Y₁+Y₂+... +Y_n-1+Y_n/2).

Наконец, заменяя трапецию на параболу, получим формулу Симпсона

для метода парабол

Iпарабол ~ (h/3)*( Y₀+4Y₁+2Y₂+4Y₃+2 Y₄... +4Y_n-1+Y_n),

причем n должно быть обязательно четным.

Все эти формулы вычисляют интеграл приближенно. Для оценки погрешности, возникающей при этих расчетах, используется правило двойного пересчета: вычисляют интеграл по выбранной квадратурной формуле дважды - сначала с некоторым шагом h, затем с шагом h/2, т. е. удваивают число n. Обозначив результаты вычислений через I_n и I_2n, сравнивают их по модулю. Если ç I_n - I_2nç < E, то полагают I ~I_2n. В противном случае расчет повторяют с шагом h/4. В качестве начальной величины шага можно рекомендовать число, близкое к Е^(1/4), учитывая что Е всегда меньше 1.

Пример 7. 1.

Пусть f(X) = 1/(1+X), a=0, b = 0, 8 и E = 0, 0001. Вычислим с помощью EXCEL определенный интеграл всеми приведенными выше методами. Как видно из формул, все они предусматривают вычисление тех или иных сумм значений f(X) с последующим умножением на коэффициенты, пропорциональные h.

Откроем новый рабочий лист. Отведем столбец А под значения Х. Исходя из численного значения Е, выберем начальное значение hнач = 0, 1. Учитывая правило двойного пересчета, положим h = 0, 05 и внесем числовой ряд по Х от 0 до 0, 8 с шагом 0, 05 в блок А3: А18, т. к. Х=0, 8 в формуле не участвует. Отведем столбцы В и С для решения по формуле прямоугольников с узлом слева. Это значит, что в ячейки В3 и С3 надо внести одну и ту же формулу =1/(1+A3). Далее формулу В ячейке В3 надо скопировать в блок В4: В18, т. е. в этом столбце вычисляются значения f(X) с шагом 0, 05. В столбце С значения f(X) надо вычислять с шагом 0, 1, т. е. формулу из ячейки С3 надо копировать в ячейки С5, С7, С9 и т. д. Проще всего это сделать так. Оставить ячейку С4 пустой и выделить блок С3: С4. Далее этот блок из двух ячеек скопировать в блок С5: С17.

Отведем строку 20 для вычисления интегралов. Занесем в ячейку В20 формулу =СУММ(В3: В18)*0, 05, где СУММ - встроенная функция EXCEL, вызываемая Мастером Функций. В ячейку С20 введем формулу =СУММ(С3: С17)*0, 1. Числа, появившиеся в этих ячейках, достаточно сильно различаются между собой.

Проведем аналогичные операции в столбцах D и Е для вычисления интеграла методом прямоугольников с узлом справа. Следует обратить внимание на то, что на этот раз в формулах отсутствуют значения, равные Х₀.

В столбцах F и G проведем вычисления интеграла методом трапеций. Здесь следует обратить внимание на формулы в строках 3 и 19. В них подынтегральная функция должна быть поделена на 2 согласно формуле трапеций.

Для метода прямоугольников с узлом в центре выделим столбцы Н и I. В ячейку Н3 должна быть введена формула =1/(1+A3+0, 025), а в ячейку I3 - формула =1/(1+A3+0, 5). Далее эти формулы должны быть скопированы до строки 18.

И, наконец, для метода парабол возьмем столбцы J и K. В столбце J вычислим интеграл с шагом 0, 05. Введем в ячейку J3 формулу =1/(1+A3), в ячейку J4 - формулу =4/(1+A4), в ячейку J5 - формулу =2/(1+A5). Далее выделим блок J4: J5 и скопируем его в блок J6: J18. Затем в ячейку J19 запишем формулу =1/(1+A19). При вычислении суммы в ячейке J20 надо не забыть, что в формуле участвует выражение h/3, а не просто h.

Что касается столбца К, то формула в ячейке К3 совпадает с ячейкой J3, в ячейке К5 подынтегральная функция должна быть умножена на 4, а в ячейке К7 - умножена на 2 и т. д., кроме ячейки К19.

Как видно из таблицы, метод парабол обладает наибольшей точностью из всех рассмотренных методов.

8. ЧИСЛЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННОГО ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ

Как известно, лишь небольшое число типов уравнений первого порядка допускает интегрирование в квадратурах. Еще реже удается получить решение в элементарных функциях. Тем большее значение имеют численные методы, позволяющие получить приближенное решение одного обыкновенного дифференциального уравнения первого порядка.

Пусть требуется найти приближенное решение уравнения

dY/dX = Y’ = f(X, Y),

удовлетворяющее начальному условию Y(X₀) = Y₀. Численное решение задачи состоит в вычислении таблицы приближенных значений Y₁, Y₂, ... , Y_nрешения уравнения Y(X) в точках Х₁, Х₂, .... , Х_n. Обычно, X_i = X₀+ih, где i=1, 2, ... , n. Точки Х_i называются узлами сетки, а величина h - шагом, причем 0< h< 1.

8. 1. Метод Эйлера.

Этот метод относится к группе одношаговых методов, в которых для расчета точки Y_i+1 = Y(X_i+1) требуется информация только о последней вычисленной точке Y_i. Формула Эйлера вычисления любого Y такова

Y_i+1 = Y_i +hf(X_i, Y_i), где i=0, 1, 2,..., n-1.

Для оценки погрешности применяется правило двойного пересчета: расчет повторяют с шагом h/2 и погрешность более точного значения Yi* при шаге h/2 оценивают так

max ç Y_i * - Y_i ç < E для i=1, 2,..., n.

Метод Эйлера называют методом первого порядка, поскольку его погрешность пропорциональна h и для вычисления новой точки решения функция f вычисляется лишь один раз.

Метод Эйлера можно усовершенствовать множеством различных способов. Из этих способов наиболее распространены два. Это так называемые исправленный и модифицированный методы Эйлера.

Обозначим К₁ = f(X_i, Y_i). Тогда оба метода описываются формулой

Y_i+1 = Y_i +hФ(X_i, Y_i), где

Ф(X_i, Y_i) = a₁K₁ + a₂f(X_i+b₁h, Y_i+b₂hK₁).

Для исправленного метода a₁= a₂=0, 5 и b₁= b₂=1.

Для модифицированного метода a₁=0, a₂=1 и b₁= b₂=0, 5.

Это методы второго порядка, погрешность решения пропорциональна h².

Пример 8. 1.

Найти решение уравнения

Y’ = 0, 25Y² + X²

c начальным условием Y(0) = -1 на отрезке [0; 0, 5] с шагом 0, 1. Точность решения принять Е=0, 0001.

Откроем новый рабочий лист EXCEL. Отведем столбец А под значения Х. Учитывая правило двойного пересчета занесем в блок А3: А13 значения Х от 0 до 0, 5 с шагом 0, 05. Значения Y по методу Эйлера с шагом 0, 05 и 0, 1 будем вычислять в столбцах B и C, для оценки погрешности отведем столбец D. Проведем для сравнения здесь же решение этой задачи исправленным методом Эйлера. Столбцы E и F отведем под значения Y_исп с шагом h и h/2, столбцы G и H - под значения коэффициента K₁, столбцы I и J - под значения функции Ф_исп, столбец К - для оценки погрешности. В ячейки В3, С3, E3 и F3 внесем начальные значения Y=-1. Основные формулы в строках 3, 4 и 5 приведены в таблице

ячейка	формула
Строка 3
B3	-1
C3	-1
D3	=ABS(C3-B3)
E3	-1
F3	-1
G3	=0, 25*E3^2+A3^2
H3	=0, 25*F3^2+A3^2
I3	=0, 5G3+0, 5(0, 25(E3+0, 05G3)^2+(A3+0, 05)^2)
J3	=0, 5H3+0, 5(0, 25(F3+0, 1H3)^2+(A3+0, 1)^2)
K3	=ABS(F3-E3)
Строка 4
B4	=B3+0, 05(0, 25B3^2+A3^2)
E4	=E3+0, 05*I3
Строка 5
C5	=C3+0, 1(0, 25C3^2+A3^2)
F5	=F3+0, 1*J3

Формулы в остальных строках получаются копированием содержимого строк, указанных в таблице. Результаты вычислений EXCEL приведены ниже. Как видно из таблицы, расчеты методом Эйлера на порядок хуже, чем расчеты исправленным методом.

8. 2. Метод Рунге-Кутта четвертого порядка.

По этому одношаговому методу вычисления проводятся по формуле

Y_i+1 = Y_i +hФ(X_i, Y_i), где

Ф(X_i, Y_i) = (K₁+2K₂+2K₃+K₄)/6

и К₁ = f(X_i, Y_i),

K₂=f(X_i+h/2, Y_i+hК₁/2),

K₃=f(X_i+h/2, Y_i+hК₂/2),

K₄=f(X_i+h, Y_i+hК₃).

Метод Рунге-Кутта имеет порядок точности h⁴ на всем отрезке интегрирования. Оценка погрешности метода очень затруднительна. Для оценки погрешности применяется правило двойного пересчета: расчет повторяют с шагом h/2 и погрешность более точного значения Yi* при шаге h/2 оценивают так

max {ç Y_i * - Y_i ç /15}< E для i=1, 2,..., n.

Пример 8. 2.

Решим задачу примера 8. 1 методом Рунге-Кутта на том же рабочем листе. Отведем блок ячеек А17: А22 под значения Х с шагом 0, 1. Соответственно, в столбце В будем вычислять Y, в столбцах С, D, E, F - значения коэффициентов К₁, K₂, K₃ и K₄. Столбец G отведем под Ф(X_i, Y_i). Основные формулы в строках 17 и 18 приведены в таблице.

ячейка	формула
С17	=0, 25*B17^2+A17^2
D17	=0, 25(B17+0, 05C17)^2+(A17+0, 05)^2
E17	=0, 25(B17+0, 05D17)^2+(A17+0, 05)^2
F17	=0, 25(B17+0, 1E17)^2+(A17+0, 1)^2
G17	=C17+2D17+2E17+F17
B18	=B17+0, 1*G17/6

Содержимое остальных ячеек в строках с 18 по 22 получается копированием из строк 17 и 18. Результаты решения приведены ниже. Для оценки погрешности следует провести те же вычисления с шагом, равным 0, 05.

8. 3. Метод прогноза и коррекции: метод Адамса.

В методах прогноза и коррекции каждое новое значение Yi определяют в два этапа. На первом определяют приближенное значение, которое называют прогнозом. Затем на втором этапе его уточняют с помощью итерационного процесса коррекции. Этот итерационный процесс продолжают до тех пор, пока не будет достигнута заданная точность решения. Таким образом, одно из достоинств метода прогноза и коррекции состоит в том, что одновременно с решением контролируется оценка погрешности.

С другой стороны, этот метод не является одношаговым, т. е. для вычисления прогноза необходимо иметь уже несколько вычисленных точек решения.

Пусть для уравнения

dY/dX = Y’ = f(X, Y),

с начальным условием Y(X₀) = Y₀найдены каким-либо способом (методом Эйлера, Рунге-Кутта и т. п. ) три последовательных значения искомой функции, так называемый начальный отрезок: Y₁, Y₂ и Y₃ для точек Х₁, Х₂ и Х₃, вычисленных с шагом h. Имея эти значения можно вычислить значения функции f₁=f(Х₁, Y₁), f₂₌f(Х₂, Y₂), f₃₌f(Х₃, Y₃) и f₀ =f(X₀, Y₀).

Метод Адамса состоит в вычислении Y₄ сначала по формуле прогноза

Y_4pred= Y₃+hФ_pred/24 = Y₃+h(55f₃-59f₂+37f₁-9f₀)/24

а затем уточнения этого значения, вычислив f_4pred=f(Х₄, Y_4pred) и применив формулу коррекции

Y_4kor= Y₃+hФ_kor/24 =Y₃+h(9f_4pred+19f₃-5f₂+ f₁)/24.

Эти формулы имеют достаточно большую точность и дают погрешность порядка h⁴. Обычно вычисляют D=ç Y_4kor - Y_4predç и если D< E, то переходят к вычислению следующей точки по тем же самым формулам, вводя переобозначения. Если же D> E, то проводят одну или несколько итераций по формуле коррекции, вычисляя f_4pred=f(Х₄, Y_4pred) и подставляя в эту формулу Y_4kor вместо Y_4pred. Как правило, для достижения заданной точности хватает одной или двух итераций.

Пример 8. 3.

Решим методом Адамса задачу примера 8. 1. Из примера 8. 2 возьмем вычисленные значения Y₁, Y₂ и Y₃. Продолжим вычисления по формулам Адамса для Х₄ и Х₅ на том же рабочем листе. Отведем блок А26: А31 под значения Х с шагом 0, 1. В блок В26: В29 занесем значения Y из примера 9. 2. В столбце С будем вычислять значения функции f на каждом шаге. В остальных столбцах будем последовательно располагать значения Ф_pred, Y_4pred, f_4pred, Ф_kor, Y_4kor, D. Необходимые для вычислений формулы приведены в таблице

ячейка	формула
C26	=0, 25*B26^2+A26^2
D29	=55C29-59C28+37C27-9C26
E29	=B29+0, 1/24*D29
F29	=0, 25*E29^2+A30^2
G29	=9F29+19C29-5*C28+C27
H29	=B29+0, 1/24*G29
I29	=ABS(E29-H29)
B30	=H29

Формулы в остальных ячейках, участвующих в вычислениях, получаются копированием. Результаты вычислений приведены в таблице

Видно, что погрешность удовлетворяет заданному значению для последних двух точек и итераций не требуется. В противном случае следовало бы воспользоваться встроенной подпрограммой EXCEL Поиск решения так, как это описано в разделе 6.

9. РЕШЕНИЕ СИСТЕМ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.

Рассмотренные в предыдущем разделе одношаговые методы могут быть использованы для решения систем обыкновенных дифференциальных уравнений или для нахождения решения одного дифференциального уравнения высокого порядка. В последнем случае введением новых переменных оно сводится к решению системы дифференциальных уравнений первого порядка. Рассмотрим последовательно решение задачи Коши и краевой задачи применительно к системам таких уравнений.

9. 1. Задача Коши.

Для получения однозначного решения системы дифференциальных уравнений должны быть заданы дополнительные условия. Их должно быть задано столько, каков порядок решаемой системы. Если все эти условия задаются в одной точке, т. е. при одном значении Х=Х₀, то такая задача называется задачей Коши. Эти дополнительные условия называются начальными условиями, а Х₀- называется начальной точкой.

Покажем применение метода Рунге-Кутта четвертого порядка для решения задачи Коши системы двух уравнений вида

dY/dX = f₁(X, Y, Z)

dZ/dX = f₂(X, Y, Z).

Начальные условия зададим в виде Y(Х₀)=Y₀ и Z(Х₀)=Z₀.

По аналогии с разделом 8. 2 запишем формулы Рунге-Кутта для приближенного решения этой системы

Y_i+1=Y_i+hФ₁= (K₁+2K₂+2K₃+K₄)/6,

Z_i+1 = Z_i+hФ₂=(L₁+2L₂+2L₃+L₄)/6,

где

K₁= f₁(X_i, Y_i, Z_i) и L₁= f₂(X_i, Y_i, Z_i),

K₂= f₁(X_i+h/2, Y_i+hK₁/2, Z_i+hL₁/2) и L₂= f₂(X_i+h/2, Y_i+hK₁/2, Z_i+hL₁/2),

K₃= f₁(X_i+h/2, Y_i+hK₂/2, Z_i+hL₂/2) и L₃= f₂(X_i+h/2, Y_i+hK₂/2, Z_i+hL₂/2),

K₄= f₁(X_i+h, Y_i+hK₃, Z_i+hL₃) и L₄= f₂(X_i+h, Y_i+hK₃, Z_i+hL₃).

В этих формулах i = 0, 1, 2,..., n-1. Для оценки погрешности используется правило двойного пересчета точно так же, как и при решении одного уравнения.

К решению подобной системы уравнений можно свести решение задачи Коши для уравнения второго порядка

d²Y/dX² = f(X, Y, dY/dX)

с начальными условиями Y(Х₀)=Y₀ и Y’(Х₀)=Z₀.

Введем новую переменную Z(X) = dY/dX. Тогда исследуемое уравнение заменяется следующей системой из двух уравнений

dZ/dX= f(X, Y, Z)

dY/dX=Z,

с начальными условиями Y(Х₀)=Y₀ и Z(Х₀)=Z₀.

Пример 9. 1.

Применяя метод Рунге-Кутта, вычислить на отрезке [1; 1, 5] таблицу значений решения уравнения

Y” +Y’/X+Y=0

с начальными условиями Y(1)=0, 77 и Y’(1)=-0, 5, выбрав шаг 0, 1 с погрешностью 0, 0001.

С помощью подстановки новой переменной Z, перейдем к решению системы уравнений

Y’=Z

Z’=-Z/X-Y,

с начальными условиями Y(1)=0, 77 и Z(1)=-0, 5.

Откроем новый рабочий лист EXCEL и выделим в нем столбцы А, В и С под переменные X, Y и Z. В последующие столбцы будем вычислять последовательно, как и в примере 8. 2, значения коэффициентов K_i, Ф₁, L_i, Ф₂. Пусть значения Х помещаются в блок А3: А8. Тогда в ячейки В3 и С3 занесем начальные значения Y(1) и Z(1). Формулы в остальных ячейках строки 3 и 4 приведены в таблице

Формулы в остальных строках решения получаются путем копирования.

Результаты решения задачи с шагом 0, 1 приведены в таблице. Для оценки погрешности полученного решения следует провести решение вновь с шагом, равным половине начального, т. е. 0, 05.

9. 2. Краевая задача: метод стрельбы.

Если при решении дифференциального уравнения высокого порядка дополнительные условия, определяющие однозначное решение, заданы при разных значениях независимой переменной, обычно в двух точках, являющихся границами области решения уравнения, то такая задача называется краевой. При этом сами дополнительные условия называются граничными или краевыми.

Рассмотрим решение краевой задачи для уравнения второго порядка

d²Y/dX² = f(X, Y, dY/dX)

с граничными условиями Y(Х₀)=Y₀ и Y(Х_n)=Y_n.

Сущность метода стрельбы заключается в сведении краевой задачи к многократному решению задачи Коши для того же уравнения с подбором недостающего начального условия Y’(Х₀)=Z₀ так, чтобы решение задачи Коши в точке Х_n совпадало бы с заданным граничным условием Y_n с заданной точностью Е.

Алгоритм метода стрельбы таков.

1) выбирается любое значение Z₀,

2) исходное уравнение второго порядка приводится к системе из двух уравнений первого порядка введением дополнительных переменных,

3) полученная система решается численным методом, например, методом Рунге-Кутта при некотором начальном значении шага h и запоминается полученное решение в точке Х_n,

4) шаг h уменьшается в два раза и вновь находится решение в точке Х_n,

5) если новое решение отличается от старого меньше, чем на заданную точность Е, то переходят к следующему этапу; иначе - возвращаются к предыдущему этапу и снова уменьшают шаг h в два раза и т. д. до тех пор, пока не будет достигнута заданная точность,

6) при выбранном значении шага, обеспечивающего необходимую точность решения, многократно решают задачу Коши, подбирая начальное условие Y’(Х₀)=Z₀ так, чтобы получаемое в точке Y(Х_n) решение отличалось от заданного краевого условия Y_n меньше, чем на заданную величину Е.

Пример 9. 2.

Решим задачу примера 10. 1 с граничными условиями Y(1)=0, 77 и Y(1, 5)=0, 49281, выбрав шаг 0, 1 с погрешностью 0, 001.

Для этого можно использовать таблицу примера 10. 1, где был запрограммирован метод Рунге-Кутта. Изменяя значение в ячейке С3, нужно добиться получения в ячейке В8 заданного граничного значения. Конечно, сначала по правилу двойного пересчета следует убедиться в том, что выбранное значение шага h достаточно для достижения необходимой точности решения.

9. 3. Краевая задача: метод прогонки.

Рассмотрим метод прогонки на примере решения уравнения второго порядка вида

Y”+p(X)Y’+q(X)Y=f(X)

на отрезке [Х₀, Х_n] с заданными граничными условиями Y(Х₀)=Y₀=А и Y(Х_n)=Y_n=В. Смысл решения заключается в расчете таблицы приближенных значений искомой функции Y(Х) в узлах Х_i= Х₀+ih, где h=(Х_n - Х₀)/n и i=1, 2,..., n-1.

Заменим приближенно в каждом внутреннем узле производные Y” и Y’ конечными центрально-разностными отношениями

Y_i“=( Y_i+1 -2Y_i + Y_i-1)/h² и Y_i‘=( Y_i+1 - Y_i-1)/(2h).

Обозначим p_i=p(Х_i), q_i=q(Х_i), f_i=f(Х_i).

Используя эти формулы, приближенно заменим исходное дифференциальное уравнение второго порядка на систему линейных алгебраических уравнений

( Y_i+1 -2Y_i + Y_i-1)/h² + p_i ( Y_i+1 - Y_i-1)/(2h) + q_iY_i = f_i,

где i=1, 2,..., n-1, Y₀=А и Y_n=В. Решив эту систему, получим таблицу приближенных значений искомой функции. При большом n непосредственное решение такой системы, например, методом Гаусса становится громоздким. Учитывая специфический вид полученной системы алгебраических уравнений, а именно- что матрица коэффициентов ее трехдиагональна, применим специальный метод решения, называемый методом прогонки.

Запишем систему в виде

a_iY_i-1+b_iY_i +c_iY_i+1 =d_i,

где a_i=1-hp_i /2, b_i = h²q_i -2, c_i =1+hp_i /2, d_i = h²f_i.

Введем дополнительные переменные

v_i = - c_i /( b_i + a_i v_i-1) и u_i= (d_i - a_i u_i-1)/(b_i + a_i v_i-1).

Чтобы сделать схему вычислений однородной, положим a₀=0 и c_n=0. Тогда v_n=0 и Y_n=u_n. Кроме того, v₀ = - c₀/b₀ и u₀ = d₀/b₀.

Тогда решение системы определяется формулой

Y_i = u_i+ v_i Y_i+1.

Пример 9. 3.

Решим задачу примера 9. 1 с граничными условиями Y(1)=0, 77 и Y(1, 5)=0, 49281, выбрав шаг 0, 1 с погрешностью 0, 001.

Как видно из условий задачи, h = 0, 1, q=1, f=0, d=0, p=1/X для всех Х.

Откроем новый рабочий лист и выделим блок А4: А9 под значения Х от 1 до 1, 5. В блок В5: В8 занесем значения 1/X, отведем столбцы С, D, E для текущих значений a_i, b_i, c_i, столбцы F и G - для значений v_i и u_i, а столбец Н - для значений Y.

Занесем числа: в ячейку F4 - ноль, в ячейки G4 и H4 - число 0, 77. Соответственно, в ячейку F9 - тоже ноль, в ячейки G9 и H9 - число 0, 49281.

Формулы ячеек в строке 5 представлены в таблице.

ячейка	формула
B5	=1/A5
C5	=1-B5*$B$2/2
D5	=$B$2^2-2
E5	=1+B5*$B$2/2
F5	=-E5/(D5+C5*F4)
G5	=-C5G4/(D5+C5F4)
H5	=G5+F5*H6

Формулы в строках 6, 7, 8 должны быть скопированы из строки 5. Результаты вычислений приведены ниже. Можно сравнить их с результатами расчетов в примере 10. 2, чтобы оценить полученную погрешность.

10. ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

Метод сеток или метод конечных разностей является одним из самых распространенных в настоящее время методов численного решения уравнений с частными производными. В его основе лежит идея замены производных конечно-разностными отношениями. Мы ограничимся случаем двух независимых переменных.

Рассмотрим в качестве примера смешанную задачу для уравнения теплопроводности: найти значения функции U(X, T), удовлетворяющие уравнению

dU/dT = Dd²U/dX²

с начальными условиями (т. е. при Т=0) U(X, 0) = f(X) и

краевыми условиями первого рода U(0, T) = g₁(T) и U(L, T) = g₂(T).

Таким образом может быть описана задача о распространении тепла в однородном стержне длины L, на концах которого поддерживается заданный температурный режим. Соответствующей заменой переменных эту задачу можно свести к каноническому уравнению при D=1 и L=1

dU/dT = d²U/dX²

Заметим, что начальные и граничные условия должны быть согласованы, т. е. U(0, 0) = f(0)= g₁(0) и U(1, 0)=f(1)= g₂(0).

Построим на плоскости X0T равномерную прямоугольную сетку с шагом h в направлении Х и шагом l - в направлении Т:

Х= ih ( i= 0, 1, 2,..., n) и T=jk (j=0, 1, 2,... ).

Обозначим Xi= ih и Tj= jk, а также U(Xi, Tj)=Ui, j. Любой узел этой сетки, номер которого (i, j), определяется координатами(Xi, Tj). Узлы сетки, лежащие на границе полуполосы Т> =0 и 0< =X< =1, называются граничными, все остальные узлы - внутренними. Начальные и краевые условия считаются заданными в граничных узлах сетки. Приближенно заменим в каждом внутреннем узле вторую частную производную по пространственной координате Х конечно-разностным отношением

(d²U/dX²)_{i, j}=( U_{i, j-1} -2U_{i, j} + U_{i, j+1})/h²,

а первую частную производную по временной координате - конечно-разностным отношением

(dU/dT)_{i, j} =( U_{i, j+1} - U_{i, j})/k.

Тогда вместо исходного дифференциального уравнения, получаем алгебраическое уравнение вида

( U_{i, j+1} - U_{i, j})/k = ( U_{i-1, j} -2U_{i, j} + U_{i+1, j})/h².

Обозначив q=k/h², приведем это уравнение к виду

U_{i, j+1} =(1-2q)U_{i, j} + q(U_{i-1, j}+U_{i+1, j}).

Задавая i=0, 1, 2,.., n и j=0, увидим, что все слагаемые в правой части этого уравнения могут быть вычислены из граничных условий. Поэтому таким образом можно вычислить все значения U на первом временном слое при j=1. Далее, задавая j=1, можно вычислить по этой формуле значения функции U во всех узлах второго временного слоя при j=2 и т. д. Такая схема вычислений называется явной. Доказано, что вычисления по этой схеме будут устойчивы, если 0< q< = 0, 5. Задавая q=0, 5, получим алгебраическое уравнение

U_{i, j+1} =(U_{i-1, j}+U_{i+1, j})/2.

Таким образом, используя это уравнение, можно вычислить значения функции U на каждом временном слое через значения на предыдущем слое.

Пример 10. 1.

Hайти значения функции U(X, T), удовлетворяющие уравнению

dU/dT = Dd²U/dX²

с начальными условиями (т. е. при Т=0) U(X, 0) = Sin(pX) и 0< X< =1,

краевыми условиями первого рода U(0, T) = 0 и U(1, T) = 0.

Выберем по аргументу Х шаг h=0, 1, т. е. n=10. Так как q=0, 5, то по аргументу Т получаем шаг k=h²/2=0, 005.

Откроем новый рабочий лист EXCEL. Отведем столбец А под номера временных слоев от 0 до, например, 25. Заполним блок А3: А28 числами от 0 до 25. Во второй строке в ячейки В2: L2 занесем значения пространственной координаты Х от 0 до 1. В блок В3: В28 и в блок L3: L28 занесем нули - значения краевых условий. В ячейку С3 занесем формулу =SIN(3, 1415*C2) и скопируем ее в блок D3: K3. Тем самым введем в нулевой временной слой начальные условия. Далее в ячейку С4 введем основную расчетную формулу, полученную из алгебраического конечно-разностного уравнения =(B3+D3)/2. Эту формулу надо скопировать в блок С4: L28.

Результаты вычислений представлены в таблице для первых 19 слоев.

Как видно, таблица малообозрима, а при увеличении количества временных слоев вообще становится неудобочитаемой. Результаты расчетов лучше всего представить в виде диаграммы. Для построения диаграммы надо выделить блок А2: L28 и вызвать Мастер Диаграмм. Появится диалог из пяти шагов. На шаге 1 из 5 следует убедиться в том, что выделен блок А2: L28 и щелкнуть по кнопке Шаг> . На шаге 2 из 5 нужно выбрать тип диаграммы - Поверхность. На шаге 3 из 5 выберем формат 1 диаграммы. Далее на шаге 4 из 5 выберем Ряды данных - в строках и в полях Отвести 0 строк введем 1 так, чтобы получилось Отвести 1 строк для меток оси Х. То же самое проделаем для оси Y - Отвести 1 столбцов для меток оси Y. На последнем шаге 5 из 5 в поле Название диаграммы введем текст “Уравнение теплопроводности”, в поле Название по оси категорий(Х) введем текст - “длина”, в поле Значений (Z)- текст”температура”, в поле Рядов (Y) - текст “слой”. Щелкнув по кнопке Закончить, получим диаграмму, примерный вид которой приведен ниже.

Бурляев Валерий Викторович

Под редакцией Корнюшко В. Ф.

Численные методы в примерах на EXCEL.

Методическое пособие по дисциплине “Программирование и численные методы”.

Рецензент - д. т. н. профессор Бахвалов Л. А.

Подписано в печать

Печать офсетн., бум. офсетн., формат 60х90/16, тираж 100 экз., заказ

117571, Москва, пр. Вернадского, 86

издательско-полиграфический центр МИТХТ