Контакты

Случайная статья

IV. ИНТЕГРАЛЫ. Теоретические вопросы. Теоретические упражнения

Стр 1 из 3Следующая ⇒

IV. ИНТЕГРАЛЫ

Теоретические вопросы

1. Понятие первообразной функции. Теоремы о первообразных.

2. Неопределенный интеграл, его свойства.

3. Таблица неопределенных интегралов.

4. Замена переменной и интегрирование по частям в неопределенном интеграле.

5. Разложение дробной рациональной функции на простейшие дроби.

6. Интегрирование простейших дробей. Интегрирование рациональных функций.

7 Интегрирование выражений, содержащих тригонометрические функции.

8. Интегрирование иррациональных выражений.

9. Понятие определенного интеграла, его геометрический смысл.

10. Основные свойства определенного интеграла.

11. Теорема о среднем.

12. Производная определенного интеграла по верхнему пределу. Формула Ньютона – Лейбница.

13. Замена переменной и интегрирование по частям в определенном интеграле.

14. Интегрирование биномиальных дифференциалов.

15. Вычисление площадей плоских фигур.

16. Определение и вычисление длины кривой, дифференциал длины дуги кривой.

Теоретические упражнения

1. Считая, что функция 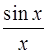равна 1 при 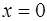, доказать, что она интегрируема на отрезке .

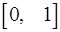2. Какой из. интегралов больше:

или ?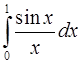

3. Пусть 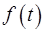– непрерывная функция, а функци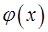и и 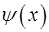дифференцируемые. Доказать, что

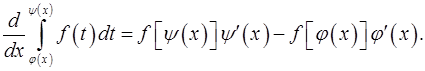
4. Найти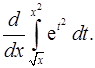

5. Найти точки экстремума функции

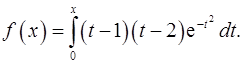
6. Пусть 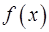– непрерывная периодическая функция с периодом 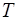. Доказать, что

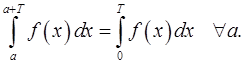
7. Доказать, что если 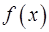– четная функция, то

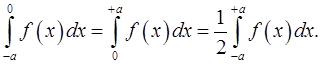
8. Доказать, что для нечетной функции 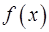справедливы равенства

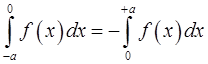и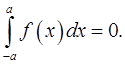

Чему равен интеграл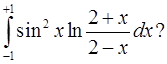

9. При каком условии, связывающем коэффициенты 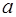, , 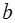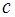интеграл 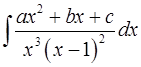является рациональной функцией?

10. При каких целых значениях 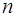интеграл 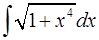выражается элементарными функциями.

12 3 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.