
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическое занятие №57. Тема: «Предел функции в точке и на бесконечности». Задание №1. Внимательно изучите теорию по данной теме и разберите приемы вычисления пределов. Перепишите в тетради все правила (выделены жирным шрифтом) и примеры 1 (а,б), 3(а,б)
Практическое занятие №57
Тема: «Предел функции в точке и на бесконечности»
Задание №1. Внимательно изучите теорию по данной теме и разберите приемы вычисления пределов. Перепишите в тетради все правила (выделены жирным шрифтом) и примеры 1 (а, б), 3(а, б), 4.
1. Предел функции. Основные приемы вычисления пределов
Предел функции
 читается так: «предел функции
читается так: «предел функции 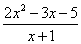 при икс стремящемся к единице».
при икс стремящемся к единице».
То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.
Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:
Пример 1:
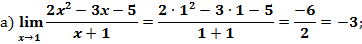
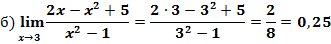
1)Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
Пример с бесконечностью: 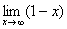
Разбираемся, что такое 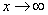 ? Это тот случай, когда
? Это тот случай, когда 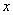 неограниченно возрастает, то есть: сначала
неограниченно возрастает, то есть: сначала 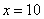 , потом
, потом 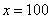 , потом
, потом 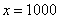 , затем
, затем 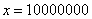 и так далее до бесконечности.
и так далее до бесконечности.
А что в это время происходит с функцией 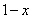 ?
?
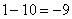 ,
, 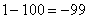 ,
, 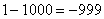 , …
, …
Итак: если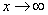 , то функция
, то функция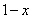 стремится к минус бесконечности:
стремится к минус бесконечности: 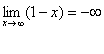
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функциюбесконечность и получаем ответ.
Еще один пример с бесконечностью: 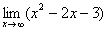
Вывод: при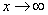 функция
функция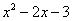 неограниченно возрастает:
неограниченно возрастает:
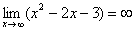
И еще серия примеров: 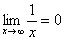 ,
, 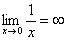 ,
, 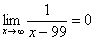 ,
, 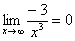 ,
, 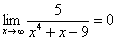 ,
, 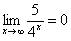 ,
, 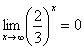 ,
, 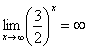 ,
, 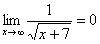 ,
, 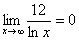
Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: 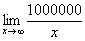 , то все равно
, то все равно 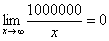 , так как рано или поздно «икс» примет такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.
, так как рано или поздно «икс» примет такие гигантские значения, что миллион по сравнению с ними будет самым настоящим микробом.
Запомните: 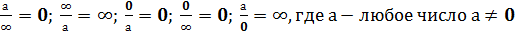
Пример 2: 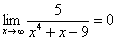
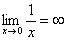
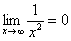
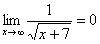
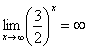
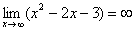
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|