История возникновения комбинаторики.

ОГБПОУ «Смоленский автотранспортный колледж им. Е. Г. Трубицына»

РЕФЕРАТ

На тему: «Комбинаторика»

Выполнил: студент 18 гр. ТОР

Голубев С. А.

Руководитель: Комарова Н. М.

Смоленск, 2022

План:

История возникновения комбинаторики. 3

Основные понятия комбинаторики. 4

Выборка. 4

Размещения и перестановки. 4

Сочетания. 4

Формула Ньютона. 5

Вывод. 7

Список литературы.. 8

История возникновения комбинаторики.

Задачи, в которых требуется из элементов конечного составлять различные комбинации, удовлетворяющее каким либо условиям, и находить число этих комбинаций называют комбинаторными. Такие задачи часто приходится решать в

Комбинаторика – это раздел математики, в котором изучаются вопросы выбора или расположения элементов множества в соответствии с заданными правилами.

Термин " комбинаторика" был введён в математический обиход знаменитым Лейбницем (1646-1716) - всемирно известный немецкий учёный, занимался философией, математикой, физикой, организовал Берлинскую академию наук и стал её первым президентом.

В 1666 году Лейбниц опубликовал " Рассуждения о комбинаторном искусстве". В своём сочинении Лейбниц, вводя специальные символы, термины для подмножеств и операций над ними находит все k -сочетания из n элементов выводит свойства сочетаний:

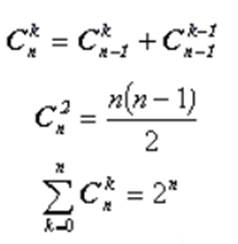
В течение всей своей жизни Лейбниц многократно возвращался к идеям комбинаторного искусства. Комбинаторику он понимал весьма широко, именно, как составляющую любого исследования, любого творческого акта, предполагающего сначала анализ (расчленение целого на части), а затем синтез (соединение частей в целое).

В XVIII веке к решению комбинаторных задач обращались выдающиеся математики. Так, Леонард Эйлер рассматривал задачи о разбиении чисел, о паросочетаниях, о циклических расстановках, о построении магических и латинских квадратов.

В 1713 году было опубликовано сочинение Я. Бернулли " Искусство предположений", в котором с достаточной полнотой были изложены известные к тому времени комбинаторные факты. " Искусство предположений" появилось после смерти автора и не было автором завершено. Сочинение состояло из 4 частей, комбинаторике была посвящена вторая часть, в которой содержатся формулы:

-для числа перестановок из n элементов

-для числа сочетаний (называемого Я. Бернулли классовым числом) без повторений и с повторениямими,

-для числа размещений с повторениями и без повторений.

Для вывода формул автор использовал наиболее простые и наглядные методы, сопровождая их многочисленными таблицами и примерами.

Сочинение Я. Бернулли превзошло работы его предшественников и современников систематичностью, простотой методов, строгостью изложения и в течение XVIII века пользовалось известностью не только как серьёзного научного трактата, но и как учебно-справочного издания. В работах Я. Бернулли и Лейбница тщательно изучены свойства сочетаний, размещений, перестановок. Перечисленные комбинаторные объекты относятся к основным комбинаторным конфигурациям.

Комбинаторика, пройдя многовековой путь развития, обретя собственные методы исследования, с одной стороны, широко используется при решении задач алгебры, геометрии, анализа, с другой стороны, сама использует геометрические, аналитические и алгебраические методы исследования. В конце XVIII века учёные, принадлежащие комбинаторной школе Гинденбурга, попытались построить общую комбинаторную теорию, используя бесконечные ряды. Исследователи этой школы изучили большое количество преобразований рядов: умножение, деление, возведение в степень, извлечение корней, обращение рядов, разложение трансцендентных функций.

В XX веке комбинаторика подверглась мощному процессу алгебраизации благодаря работам Дж. -К. Рота (1964), а затем Р. Стенли. Изучение ими частично упорядоченных множеств, свойств функции Мёбиуса, абстрактных свойств линейной зависимости, выявление их роли при решении комбинаторных задач способствовали обогащению комбинаторных методов исследования и дальнейшей интеграции комбинаторики в современную математику.

Основные понятия комбинаторики

Выборка

Размещения и перестановки

Сочетания

Формула Ньютона

Вывод

Список литературы