Задачи на оптимальный выбор. Решение.

Задачи на оптимальный выбор

№1. В 1-е классы поступает 45 человек: 20 мальчиков и 25 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом ― 23. После распределения посчитали процент девочек в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей?

Решение.

Решение 1. Вместо суммарного процента будем считать суммарную долю девочек ― очевидно, эти числа отличаются в 100 раз и достигают своего максимума одновременно. Каждая девочка в классе из 22 человек составляет 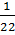от общего числа учащихся в этом классе, а в классе из 23 человек ― 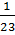от общего числа учащихся. Значит, если поменять местами девочку из большего класса и мальчика из меньшего, суммарный процент девочек вырастет. Таким образом, максимум достигается, когда все подобные перестановки сделаны, то есть, когда меньший класс полностью состоит из девочек, а в большем классе ― 3 девочки и 20 мальчиков.

№2. В 1-е классы поступает 43 человека: 23 мальчика и 20 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом ― 21. После распределения посчитали процент мальчиков в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей?

12 3 4 Следующая ⇒