Пирамида. Особенные пирамиды

Дисциплина МАТЕМАТИКА

Группы 1 курса

Преподаватель Мартусевич Татьяна Олеговна

Форма коммуникации VK

Теоретическая часть

Изучите конспект. Посмотрите видео урок:

https: //www. youtube. com/watch? v=Y_Z3ciD1rQM& ab_channel=LiameloNSchool

Сделайте конспект. Можно распечатать, вклеить в тетрадь, добавить информацию из видео урока.

Пирамида

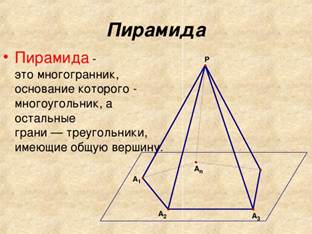
Правильная пирамида

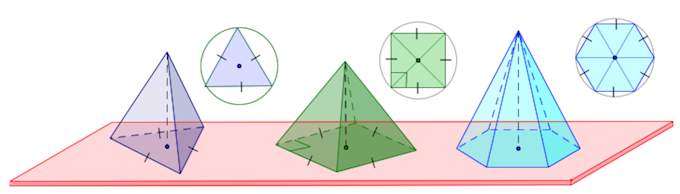
Пирамида называется правильной, если в её основании лежит правильный многоугольник, а вершина проецируется в центр основания.

На рисунке изображены треугольная пирамида (тетраэдр), четырехугольная и шестиугольная правильные пирамиды.

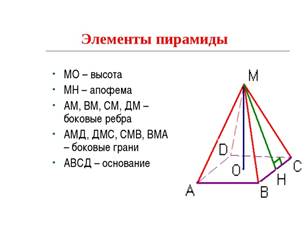
С помощью презентации «Правильная пирамида» самостоятельно в тетради постройте правильную треугольную пирамиду и выделите цветными карандашами все её элементы. Сначала изобразите основание, затем проведите в нем медианы, затем из точки их пересечения вертикально вверх высоту и только после этого – боковые рёбра. Используйте пунктирные и сплошные линии.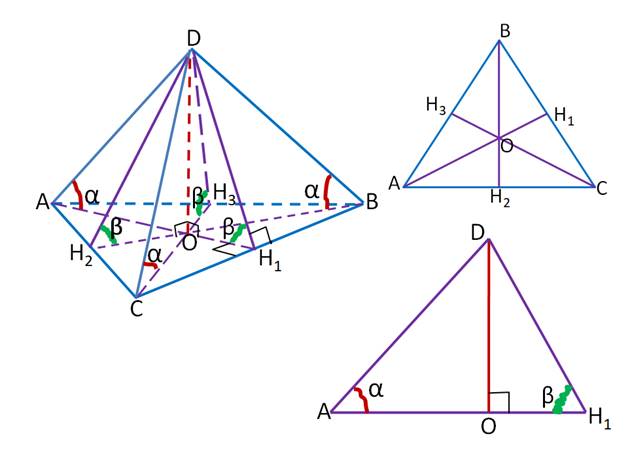

Теперь также самостоятельно постройте в тетради правильную четырёхугольную пирамиду. Отметьте углы α - между ребрами и основанием и β - между гранями и основанием пирамиды.

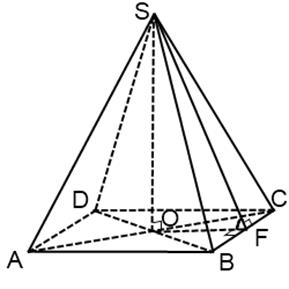
Площадь боковой и полной поверхности пирамиды и объём пирамиды:

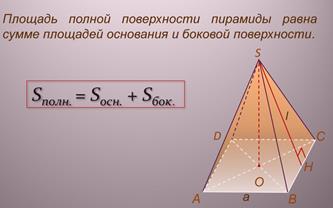
Запишите и выучите формулы нахождения площади боковой поверхности, площади полной поверхности и объёма пирамиды. Сравните с аналогичными формулами для призмы.

Также для решения задач необходимо вспомнить формулы площадей плоских фигур (распечатать и вклеить в тетрадь или переписать):

Особенные пирамиды

Теорема 1. Если боковые ребра пирамиды равны (или равнонаклонены к плоскости основания), то вершина пирамиды проецируется в центр описанной окружности (основание высоты пирамиды совпадает с центром описанной окружности)

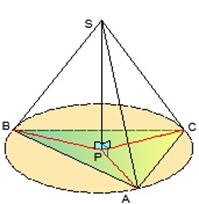
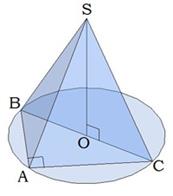
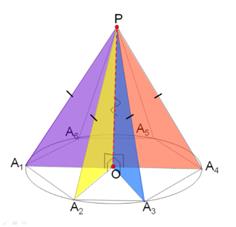
Теорема 2.

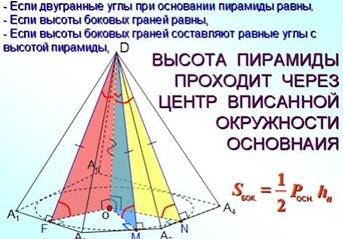
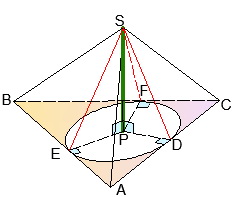
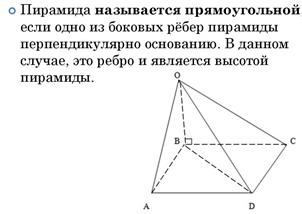
Прямоугольная пирамида

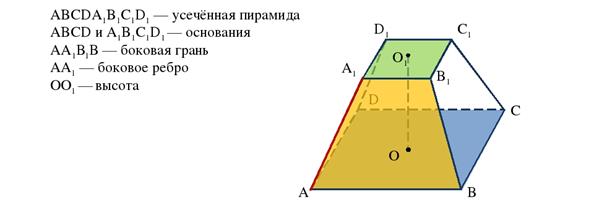
Усеченная пирамида – это часть полной пирамиды, заключенная между основанием пирамиды и секущей плоскостью, параллельной основанию.

В правильной усеченной пирамиде основания – правильные многогранники, а высота соединяет центры оснований.