
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Л.З. № 3 Определение площадей по карте с помощью палетки и планиметра
Л. З. № 3 Определение площадей по карте с помощью палетки и планиметра
Цель: познакомиться с определением площадей по карте с помощью палетки и планиметра.
Ход работы.
1. Ознакомиться с теоретическим материалом.
2. Законспектировать теоретический материал.
3. Зарисовать и описать схемы и рисунки.
4. Изготовить палетку. Провести измерение с помощью палетки.
Теоретический материал.
Аналитический способ. Если участок представляет собой замкнутый многоугольник, то, сняв с плана прямоугольные координаты его вершин, площадь участка вычисляют по формуле:
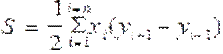
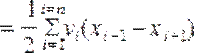 ,
,
где i - номера вершин многоугольника, пронумерованных по ходу часовой стрелки.
По этой же формуле можно вычислить площадь с криволинейными границами, если координаты точек границы сняты так часто, что отрезки между точками можно считать прямыми. В последнем случае съём координат выполняют с помощью специального прибора – дигитайзера, а вычисления выполняют на ЭВМ.
Графические способы. Участок на плане разбивают на простые геометрические фигуры (обычно – треугольники), элементы которых измеряют с помощью измерителя и поперечного масштаба, а площади вычисляют по известным формулам и суммируют.
Разбиение площади на простые фигуры выполняют также, применяя палетки. Палетка – лист прозрачного материала (восковки, лавсана, пластика), на который нанесена сетка квадратов размером 2× 2 мм или система равноотстоящих параллельных линий.
Палетку накладывают на фигуру, площадь которой должна быть определена (рисунок 2) и подсчитывают число больших квадратов (m1) и полных малых квадратов (m2), закрывающих фигуру. Затем суммируют неполные малые квадраты (m3). Площадь фигуры равна произведению цены деления палетки (t) на полную сумму делений:
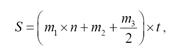
где n - число малых квадратов в большом.
Палеткой с параллельными линиями площадь делится на трапеции, в каждой из которых измеряют длину средней линии. Суммируя площади трапеций, равные произведению длины средней линии на расстояние между линиями, определяют площадь участка.
Точность определения площади с помощью палеток - 1/50.
Полярный планиметр. Планиметрами называются приборы для измерения площадей. Наиболее распространён полярный планиметр. Он состоит из двух рычагов – полюсного 1 и обводного 4, соединяемых шарниром 8. Полюс планиметра (массивный цилиндр 2 с иглой, втыкаемой в бумагу) в процессе измерения площади остается неподвижным. На конце длинного плеча обводного рычага укреплен шпиль 3 (или лупа с маркой в виде креста в ее центре), которым обводят контур измеряемой площади. На коротком плече обводного рычага крепится каретка с мерным колесиком 6, опирающимся на поверхность бумаги, и счетным механизмом. Когда обводной шпиль 3 (или марка) перемещается по линии контура перпендикулярно рычагу, мерное колесико 6 катится по бумаге. При перемещении обводного шпиля по направлению рычага колесико скользит по бумаге, не вращаясь. При перемещении шпиля в иных направлениях происходит и вращение, и скольжение. Суммарное число оборотов колесика, накопленное при обводке шпилем контура, пропорционально площади, ограниченной контуром.
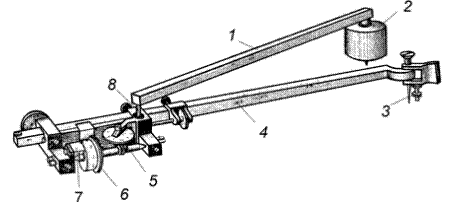
Рис. 1. Полярный планиметр
Для подсчета числа оборотов вращение колесика передается на циферблат 5. По ободу колесика нанесено 100 делений. Отсчеты по шкале обода берут с помощью верньера 7. Отсчет по планиметру состоит из отсчета числа целых оборотов колесика по циферблату (на рисунке – цифра 6), отсчета десятых и сотых долей оборота - по шкале обода против нуля верньера (цифры 4 и 2) и тысячных долей оборота – по номеру штриха верньера, совпадающего со штрихом на шкале обода (цифра 2).
Для измерения площади, обводят её контур, делая при этом два отсчёта по планиметру: один n1- до обвода, другой n2- после. Площадь вычисляют по формуле
S = c·(n2- n1), (4. 3)
где c – цена деления планиметра. Для надёжности площадь измеряют 3 - 5 раз и полученные результаты осредняют.
Если во время измерений полюс планиметра располагался внутри измеряемой площади, то вместо формулы (4. 3) используют формулу
S = c·(n2- n1+ Q),
где Q - постоянная планиметра.
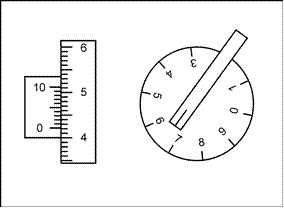
Рис. 2. Отсчет по планиметру
Цена деления планиметра c зависит от длины обводного рычага и регулируется перемещением по нему каретки с мерным колёсиком и счётным механизмом. Перед измерением площади цену деления планиметра определяют. При этом, расположив полюс в стороне, обводят фигуру, площадь S0которой известна (например, квадрат километровой сетки на карте) и вычисляют цену деления
с = S0/(n2- n1).
Для определения постоянной Q обводят фигуру с известной площадью, поместив полюс внутри этой площади, после чего вычисляют
Q = (S0 /c) - (n2- n1).
Точность определения площади планиметром - 1/300.
Электронные планиметры. Электронный полярный планиметр устроен подобно механическому, но имеет электронное счетное устройство и жидкокристаллический дисплей.
Электронный роликовый планиметр катится на двух высокофрикционных абразивных роликах, измеряющих смещения по направлению качения. Поворотная штанга с курсором, перемещаемым по контуру площади, измеряет смещения в поперечном направлении. Счетное устройство вычисляет площадь и высвечивает ее величину на дисплее.
Электронный роликовый планиметр-дигитайзер позволяет, кроме измерения площади, снимать координаты точек и решать некоторые задачи – определение радиуса окружности, длины дуги, площади сегмента и др. Возможна связь с компьютером через стандартный интерфейс.
Задание При помощи палетки определить площадьфигуры, снятой с карты масштаба 1: 10000 (см. рисунок 2). Цена наименьшего деленияпалетки (2x2 мм) для картымасштаба 1: 10000 будет равна:
t = 20x20 м = 400 м = 0, 04 Га.

Вывод:
Результаты подсчета числа квадратов палетки, содержащихся в заданной фигуре, таковы:
m1 = 7x25 =175; m2 = 61; m3 = 67.
Таким образом, общая площадь фигуры будет равна
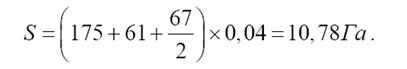
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|