МИНОБРНАУКИ РОССИИ. Санкт-Петербургский государственный. электротехнический университет. «ЛЭТИ» им. В.И. Ульянова (Ленина). Кафедра Фотоники. по лабораторной работе №5. по дисциплине «Информационные технологии». Цель работы.. Блок-схема алгоритмов

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В. И. Ульянова (Ленина)

Кафедра Фотоники

отчет

по лабораторной работе №5

по дисциплине «Информационные технологии»

Тема: бинарный поиск

Студент гр. 1204		Тупиков Е. В.
Преподаватель		Костик Н. Р.

Санкт-Петербург

Цель работы.

Изучение алгоритмов бинарного поиска, его реализация в среде Matlab на векторе исходных данных и векторе случайных чисел (изучение и программирование стандартного алгоритма «бинарного поиска»).

Блок-схема алгоритмов

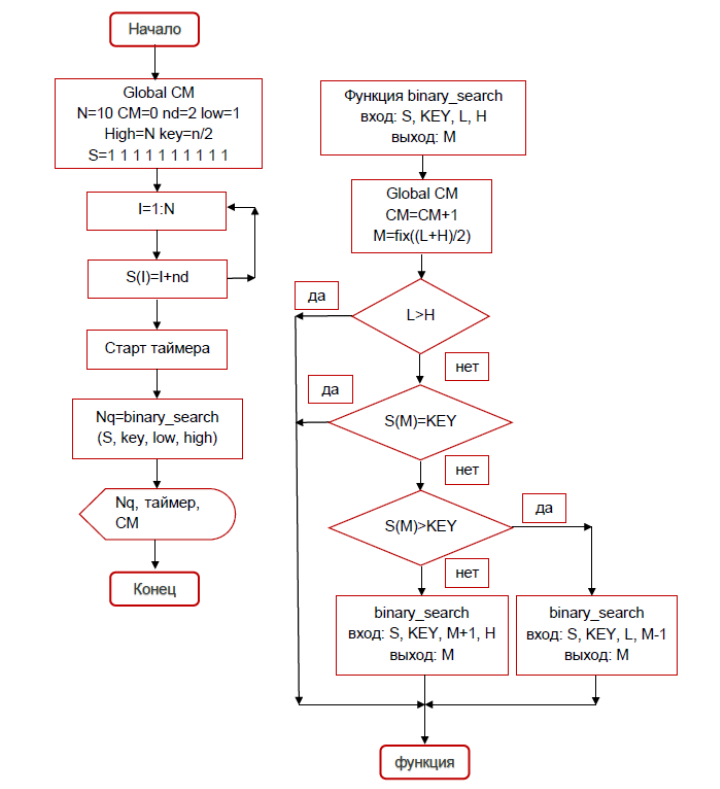
Рисунок 1. Блок-схема бинарного поиска

Код программы

global cm

cm=0;

nd=2; %shag

low=1; %nijniy segment

n = input('Vvedite dlinnu stroki: '); %zadacha dlini massiva

length=n;

S=ones(1, length); %vvodim vektor, sostoyashiy is edenic

N=numel(S);

key=round(N/2); %vibor kluchevogo elementa

for i=1: N %zapolnyaem massiv tak, chtobi on bil otsortirovan po vozrastaniyu

S(i)=i+nd;

end

tic

Nq=binary_search(S, key, low, N);

toc

disp(" dlina massiva: " );

disp(length);

disp(" key found at number: " );

disp(Nq);

disp(" number of function calls: " );

disp(cm);

Код функции

function M=binary_search(S, KEY, L, H)

global cm

cm=cm+1;

M=fix((L+H)/2); %elrment is seredini

if L< =H %esli granici ne somknulis

if S(M)~=KEY

if S(M)> KEY

M=binary_search(S, KEY, L, M-1); %poisk v pervoi polovine massiva

else

M=binary_search(S, KEY, M+1, H); %poisk vo vtoroi polovine massiva

end

Результаты

Бинарный поиск

Рисунок 2. Поиск в массиве пробного (10) вектора

Рисунок 3. Поиск в массиве длиной 100.

Рисунок 4. Поиск в массиве длиной 1000.

Рисунок 5. Поиск в массиве длиной 10000.

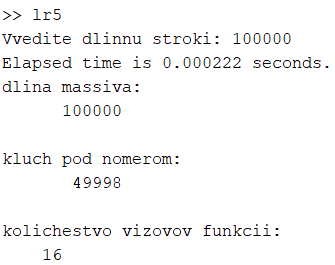
Рисунок 6. Поиск в массиве длиной 100000.

Рисунок 7. Поиск в массиве длиной 1000000.

Рисунок 8. Поиск в массиве длиной 10000000.

Таблица 1. Данные с размерностью вектора, логарифмом размерности вектора, временем выполнения сортировки и количеством вызовов функции

i	N	lg N	t*10⁴сек	cm	A
			10. 56
			6. 01
			1. 64
			1. 97		3. 25
			2. 22		3. 2
			6. 4		3. 166667
			1. 08		3. 285714

Вывод: В ходе данной работы был изучен алгоритм бинарного поиска элемента отсортированного массива и реализован в среде Matlab на примере последовательностей, являющихся арифметическими прогрессиями с длинами 10, 100, 1000, 10000, 100000, 1000000, 10000000. Были получены зависимости времен выполнения алгоритма и количества вызовов функции binary_search от длины массива. Исходя из данных можно сказать, что коэффициент пропорциональности А (cm=А lg N) – величина постоянная. Следовательно, время выполнения в среднем возрастает асимптотически как О(log n), а данная зависимость является одной из самых медленно растущих. Это показывает высокую эффективность алгоритма.