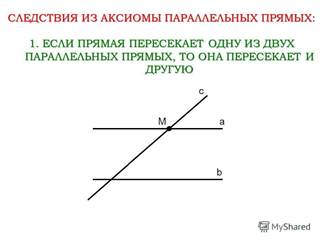
11 февраля. Тема. Аксиома параллельных прямых.. Аксиома параллельных прямых.. Задача (не записывать)

11 февраля. Тема. Аксиома параллельных прямых.

Цели: дать представление об аксиомах геометрии; ввести аксиому параллельных прямых и следствия из нее.

Ход урока

Записать в тетрадях:

Одиннадцатое февраля

Классная работа

Аксиома параллельных прямых.

Аксиомами называются те основные положения геометрии, которые не требуют доказательства, на основе которых доказываются далее теоремы и строится вся геометрия.

Задача (не записывать)

Через точку М, не лежащую на прямой а, провести прямую, параллельную прямой а. Сколько таких прямых можно провести?

- В геометрии Евклида, изложенной им в книге «Начала» ответ на данный вопрос следует из знаменитого пятого постулата, и этот ответ таков: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной. Пятый постулат знаменит тем, что долгие годы его пытались доказать на основе остальных аксиом Евклида. И лишь в прошлом веке, во многом благодаря великому русскому математику Н. И. Лобачевскому, было доказано, что пятый постулат не может быть выведен из остальных аксиом. Поэтому утверждение о единственности прямой, проходящей через данную точку параллельно данной прямой, принимается в качестве аксиомы.

Записать в тетрадях:

Следствиями называются утверждения, которые выводятся непосредственно из аксиом или теорем.

Решим задачи № 196 (устно), №197 (устно), №198.

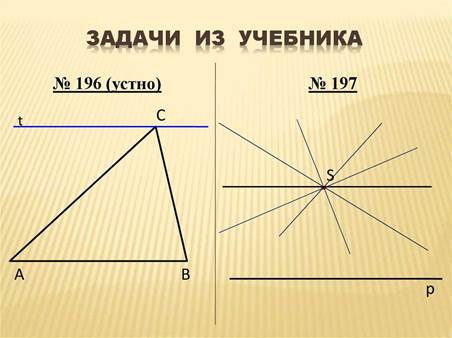
№196

По аксиоме параллельных прямых через точку С, не лежащую на АВ, можно провести только одну прямую параллельную стороне АВ. Это прямая t.

№197

1) все четыре прямые пересекают прямую р. Объясните почему?

2) одна из четырех прямых параллельна прямой р, а три другие прямые пересекают ее.

Ответ: по крайней мере, три прямые пересекают прямую р.

Записать в тетрадях:

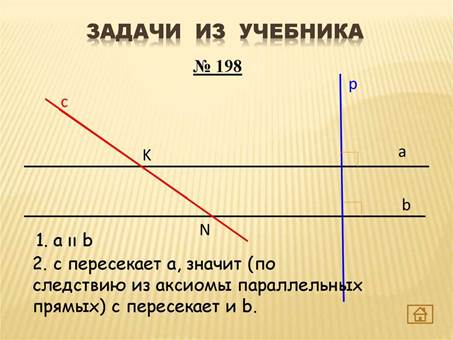
Объясните в решении, почему а ǁ b?

Домашнее задание

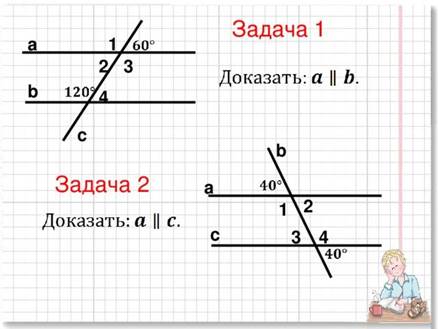
Изучить пункты 27 и 28; решить задачи № 199; задача 1; задача 2 по готовым чертежам.