
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Метод интервалов (решение квадратных и более сложных неравенств). Главное.
Метод интервалов (решение квадратных и более сложных неравенств). Главное.
Технология:
1. Всё – в левую часть, чтобы в правой части остался ноль.
2. Левую часть неравенства разложить на множители.
! Найти, при каком значении х обращается в ноль каждый множитель.
! Отметить эти точки на оси х. Если неравенство строгое, то все эти точки – выколотые.
3. Эти точки разобьют всю числовую ось (ось х) на несколько интервалов. Для каждого интервала определить знак (+ или ─ ) левой части неравенства и отметить на схеме.
4. Выделить штриховкой нужные интервалы.
! Если неравенство нестрогое и есть множители в чётных степенях, над разрешёнными (не выколотыми) ‘узловыми точками’ поставить восклицательные знаки.
5. Прочитать и записать ответ.
Примеры решений.

См. ниже


См. ниже
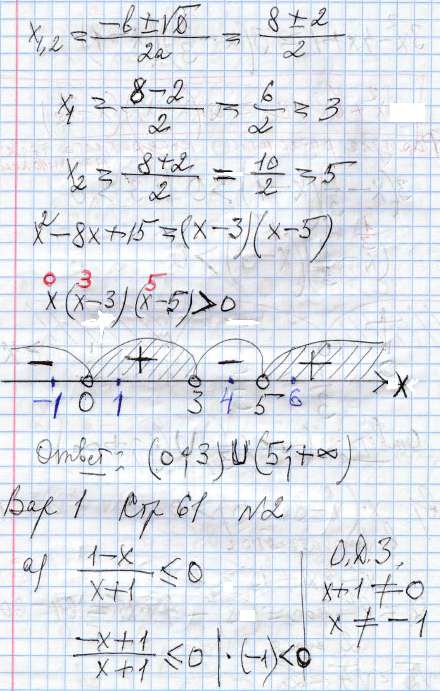
(сокращено) См. ниже
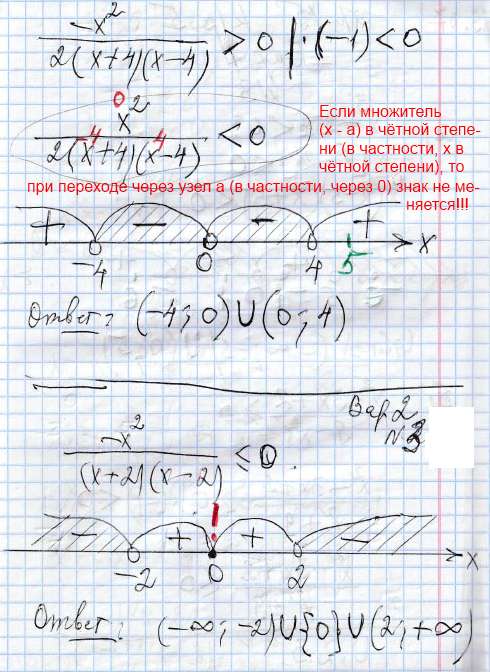
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|