
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Контрольная работа по математике (1 семестр)
Часть 1
1. Для данного определителя вычислить миноры и алгебраические дополнения элементов 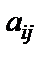 . Вычислить определитель путем разложения по k-той строке
. Вычислить определитель путем разложения по k-той строке
1. 1
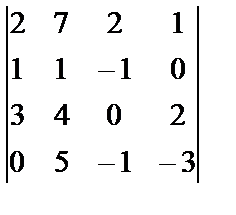 i=4, j=1, k=3
i=4, j=1, k=3
| 1. 2
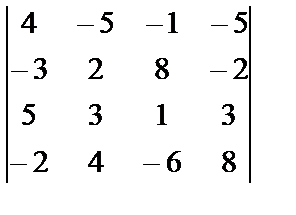 i=1, j=3, k=2
i=1, j=3, k=2
| 1. 3
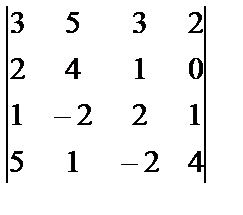 i=3, j=2, k=4
i=3, j=2, k=4
| 1. 4
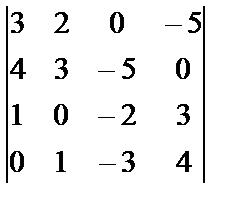 i=2, j=1, k=3
i=2, j=1, k=3
| 1. 5
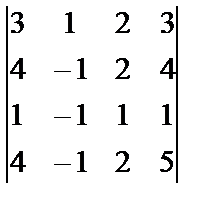 i=2, j=3, k=2
i=2, j=3, k=2
|
1. 6
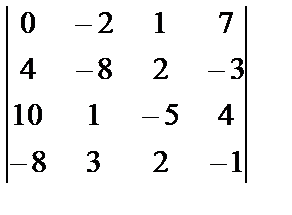 i=3, j=1, k=1
i=3, j=1, k=1
| 1. 7
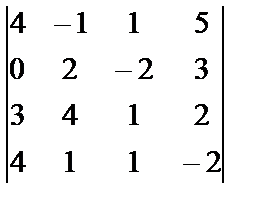 i=2, j=4, k=3
i=2, j=4, k=3
| 1. 8
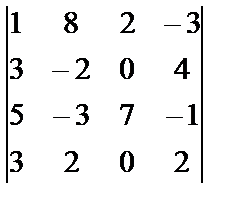 i=1, j=4, k=2
i=1, j=4, k=2
| 1. 9
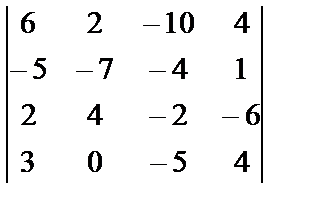 i=3, j=2, k=4
i=3, j=2, k=4
| 1. 10
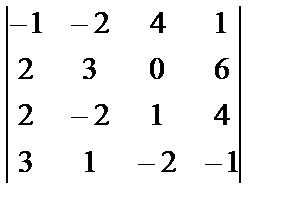 i=2, j=4, k=3
i=2, j=4, k=3
|
2. Проверить, является ли система алгебраических уравнений совместной, и если является, решить ее методом обратной матрицы
2. 1
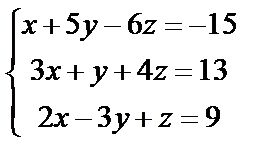
| 2. 2
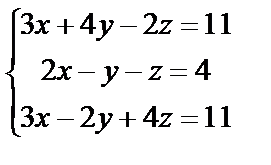
| 2. 3
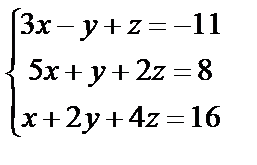
| 2. 4
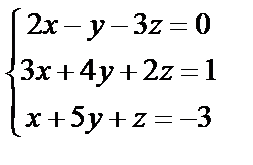
| 2. 5
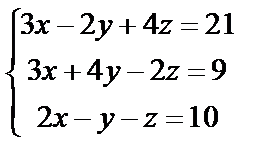
|
2. 6
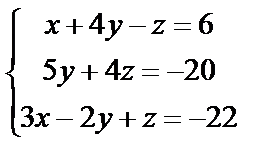
| 2. 7
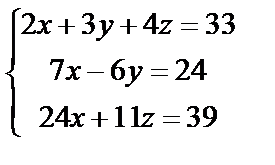
| 2. 8
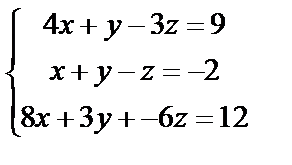
| 2. 9
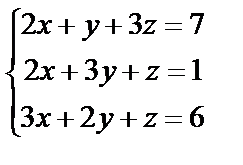
| 2. 10
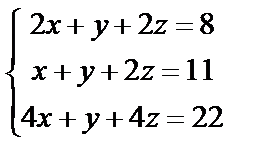
|
3. Решить однородную систему линейных уравнений. Если система имеет бесконечное множество решений, записать ее фундаментальное решение
3. 1
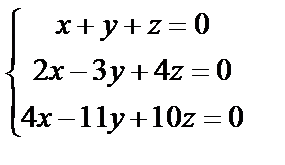
| 3. 2
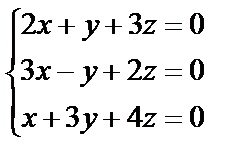
| 3. 3
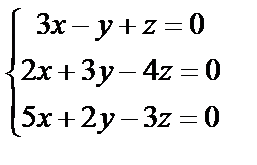
| 3. 4
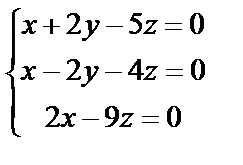
| 3. 5
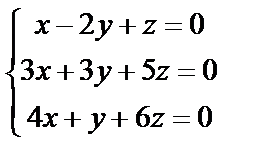
|
3. 6
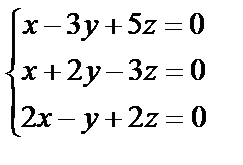
| 3. 7
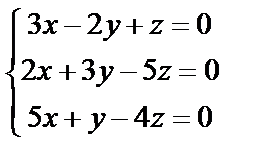
| 3. 8
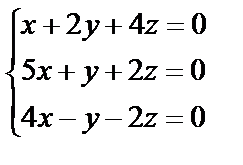
| 3. 9
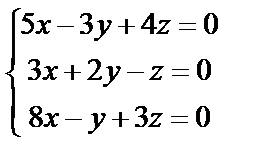
| 3. 10
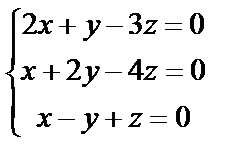
|
4. Показать, что векторы 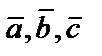 образуют базис, и найти координаты вектора
образуют базис, и найти координаты вектора 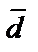 в этом базисе
в этом базисе
4. 1
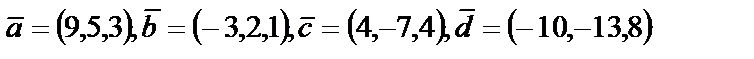
| 4. 2
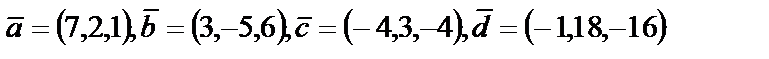
|
4. 3
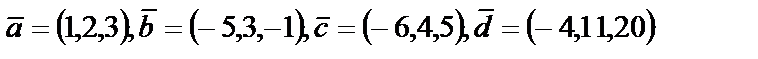
| 4. 4
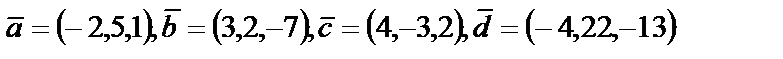
|
4. 5
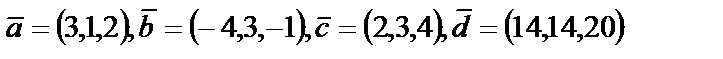
| 4. 6
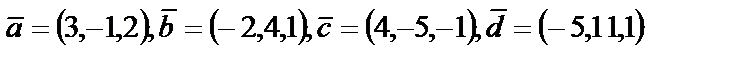
|
4. 7
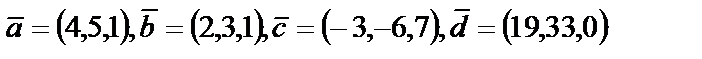
| 4. 8
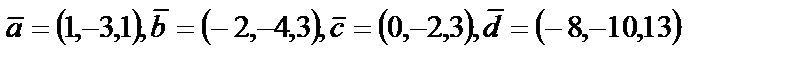
|
4. 9
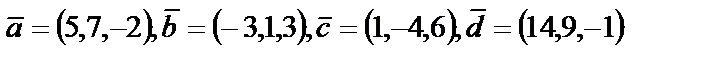
| 4. 10
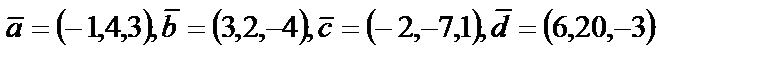
|
5. Даны векторы 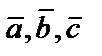 . Необходимо: а) проверить, будут ли компланарны векторы; б) найти модуль векторного произведения; в) вычислить скалярное произведение векторов
. Необходимо: а) проверить, будут ли компланарны векторы; б) найти модуль векторного произведения; в) вычислить скалярное произведение векторов
5. 1
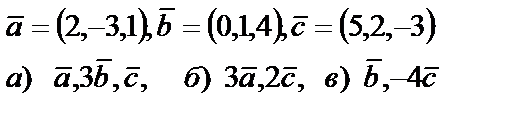
| 5. 2
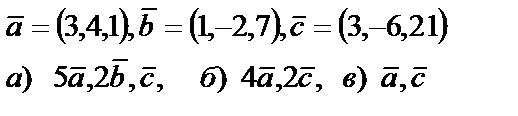
|
5. 3
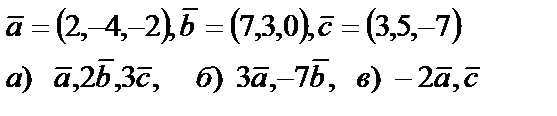
| 5. 4
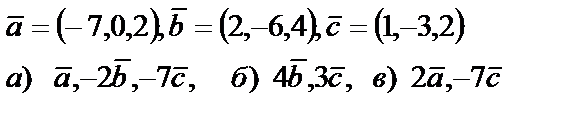
|
5. 5
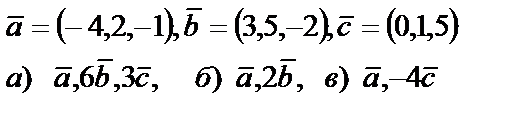
| 5. 6
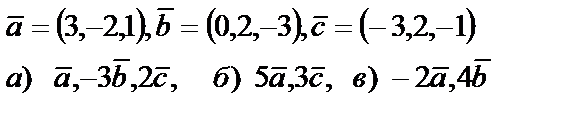
|
5. 7
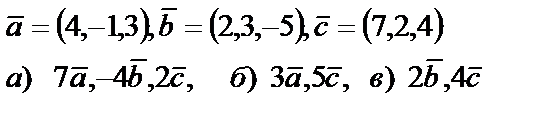
| 5. 8
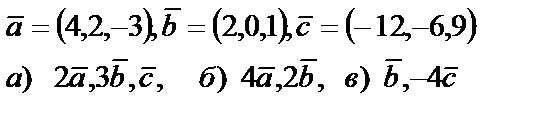
|
5. 9
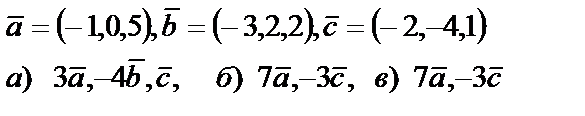
| 5. 10
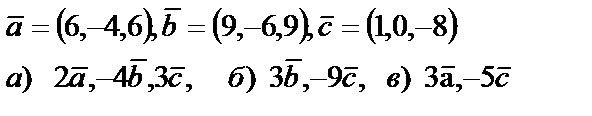
|
6.
6. 1 Найти уравнение прямой, проходящей через точку пересечения прямых 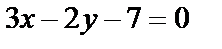 и и 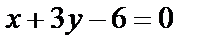 и отсекающей на оси абсцисс отрезок, равный 3. и отсекающей на оси абсцисс отрезок, равный 3.
|
| 6. 2 Найти проекцию точки А(-8, 12) на прямую, проходящую через точки В(2, -3) и С(-5, 1). |
| 6. 3 Даны две вершины треугольника АВС: А(-4, 4), В(4, -12)и точка М(4, 2) пересечения его высот. Найти вершину С. |
6. 4 Найти уравнение прямой, отсекающей не оси ординат отрезок, равный 2, и параллельной прямой 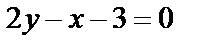 . .
|
6. 5 Найти уравнение прямой, проходящей через точку А(2, -3) и точку пересечения прямых 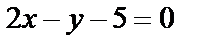 и и 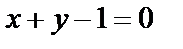 . .
|
| 6. 6 Доказать, что четырехугольник ABCD – трапеция, если А(3, 6), В(5, 2), С(-1, -3) и D(-5, 5). |
| 6. 7 Найти уравнение прямой, проходящей через точку А(3, 1) перпендикулярно прямой ВС, если В(2, 5), С(1, 0). |
| 6. 8 Найти уравнение прямой, проходящей через точку А(-2, 1) параллельно прямой MN, если M(-3, -2), N(1, 6). |
6. 9 Найти точку, симметричную точке M(2, -1) относительно прямой 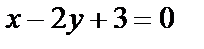 . .
|
| 6. 10 Найти точку пересечения диагоналей четырехугольника ABCD, если А(-1, -3), В(3, 5), С(5, 2) и D(3, -5). |
7. Даны четыре точки 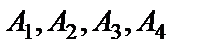 . Составить уравнения:
. Составить уравнения:
a) плоскости 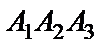 ;
;
b) прямой 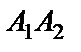 ;
;
c) прямой 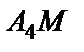 , перпендикулярной плоскости
, перпендикулярной плоскости 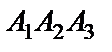 ;
;
d) прямой 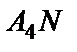 , параллельной прямой
, параллельной прямой 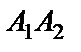 .
.
7. 1
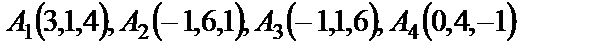
| 7. 2
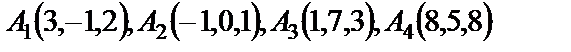
|
7. 3
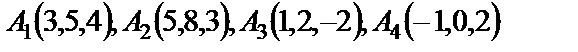
| 7. 4
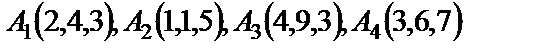
|
7. 5
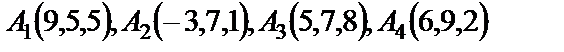
| 7. 6
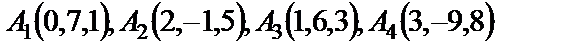
|
7. 7
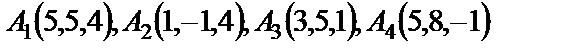
| 7. 8
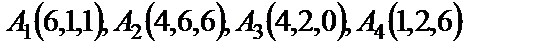
|
7. 9
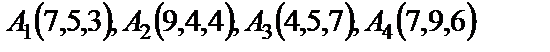
| 7. 10
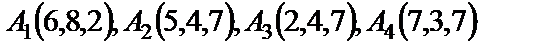
|
8. Вычислить пределы функций, не используя правила Лопиталя
| 8. 1 | а) 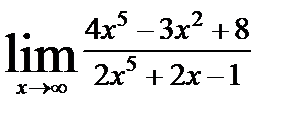
| б) 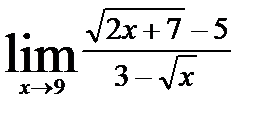
| в) 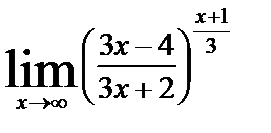
|
| 8. 2 | а) 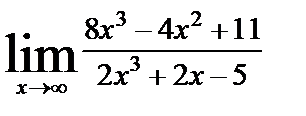
| б) 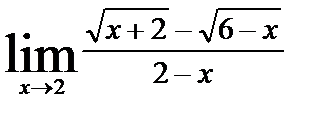
| в) 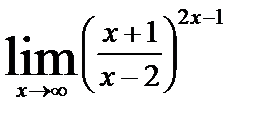
|
| 8. 3 | а) 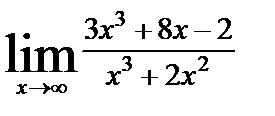
| б) 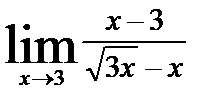
| в) 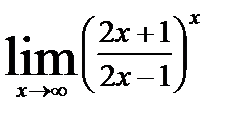
|
| 8. 4 | а) 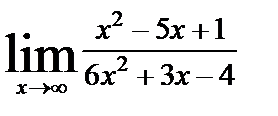
| б) 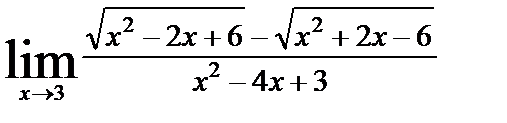
| в) 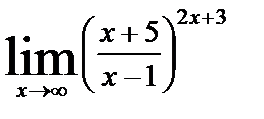
|
| 8. 5 | а) 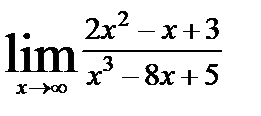
| б) 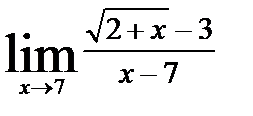
| в) 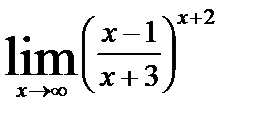
|
| 8. 6 | а) 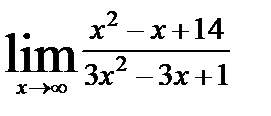
| б) 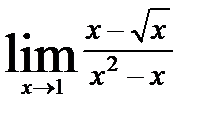
| в) 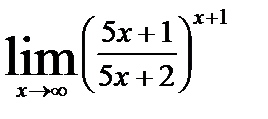
|
| 8. 7 | а) 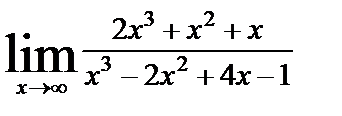
| б) 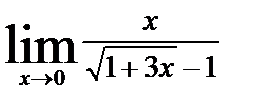
| в) 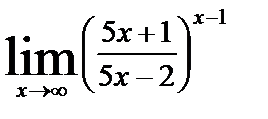
|
| 8. 8 | а) 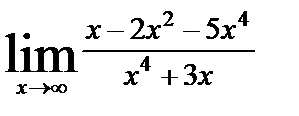
| б) 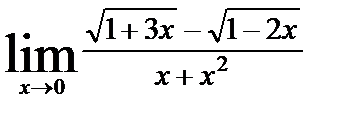
| в) 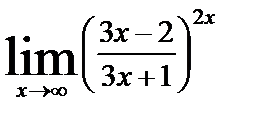
|
| 8. 9 | а) 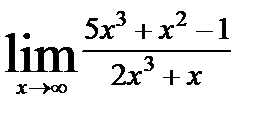
| б) 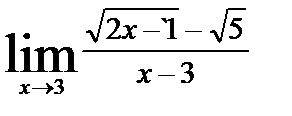
| в) 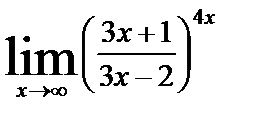
|
| 8. 10 | а) 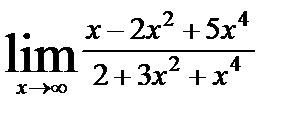
| б) 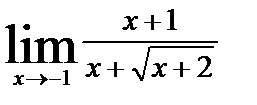
| в) 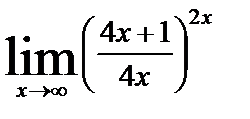
|
9. Исследовать функции на непрерывность и построит их графики
9. 1 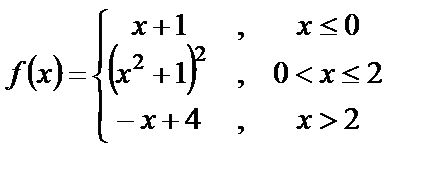
| 9. 2 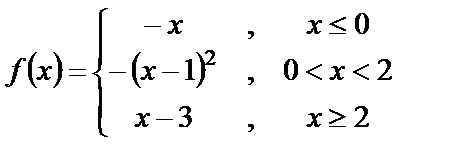
|
9. 3 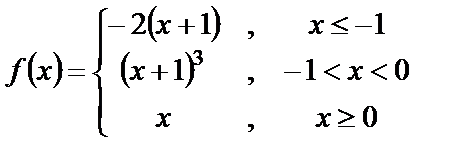
| 9. 4 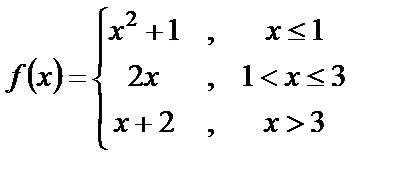
|
9. 5 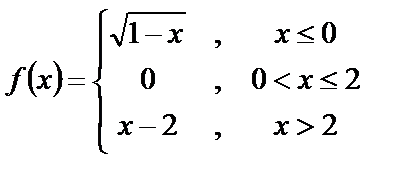
| 9. 6 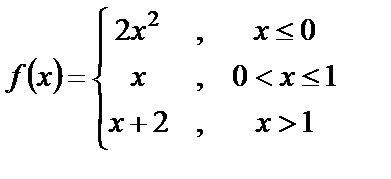
|
9. 7 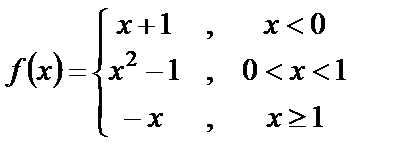
| 9. 8 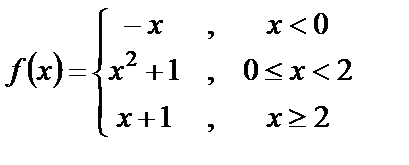
|
9. 9 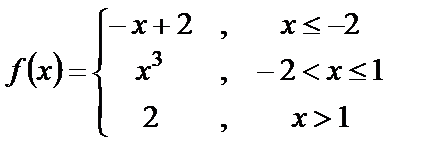
| 9. 10 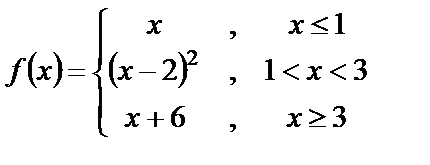
|
10. Вычислить производные следующих функций
| 10. 1 | а) 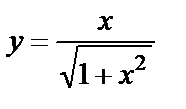
| б) 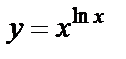
| в) 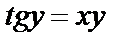
|
| 10. 2 | а) 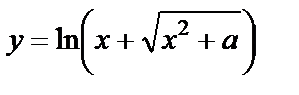
| б) 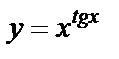
| в) 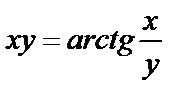
|
| 10. 3 | а) 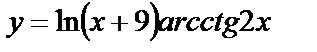
| б) 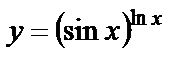
| в) 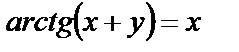
|
| 10. 4 | а) 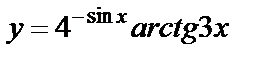
| б) 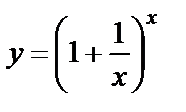
| в) 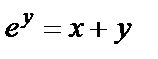
|
| 10. 5 | а) 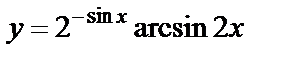
| б) 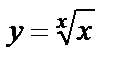
| в) 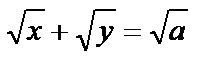
|
| 10. 6 | а) 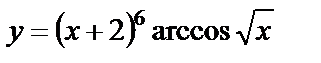
| б) 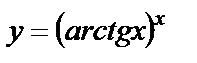
| в) 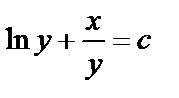
|
| 10. 7 | а) 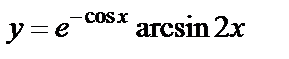
| б) 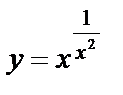
| в) 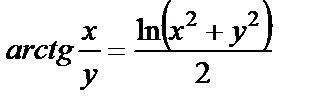
|
| 10. 8 | а) 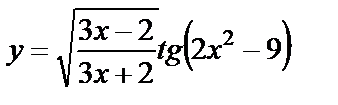
| б) 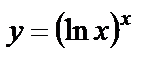
| в) 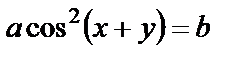
|
| 10. 9 | а) 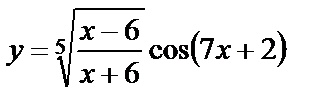
| б) 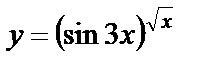
| в) 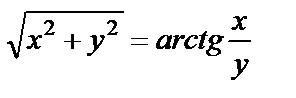
|
| 10. 10 | а) 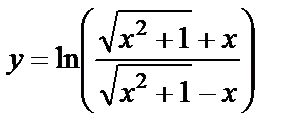
| б) 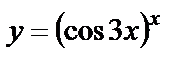
| в) 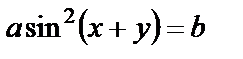
|
11. Вычислить вторую производную функции, заданной параметрически
11. 1 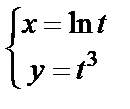
| 11. 2 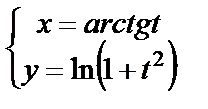
|
11. 3 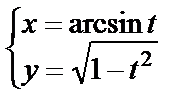
| 11. 4 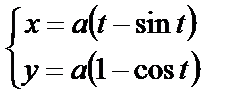
|
11. 5 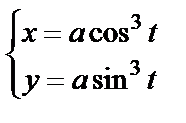
| 11. 6 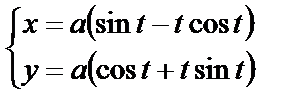
|
11. 7 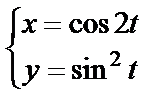
| 11. 8 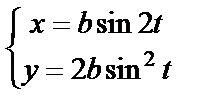
|
11. 9 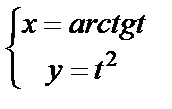
| 11. 10 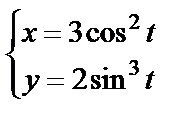
|
12. Раскрыть неопределенность, используя правила Лопиталя
12. 1 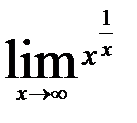
| 12. 2 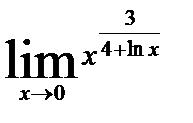
|
12. 3 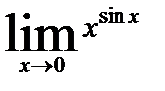
| 12. 4 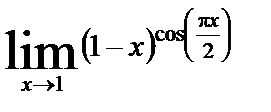
|
12. 5 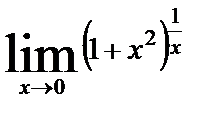
| 12. 6 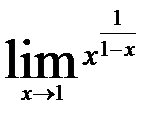
|
12. 7 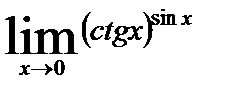
| 12. 8 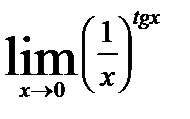 
|
12. 9 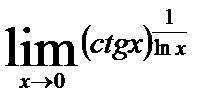
| 12. 10 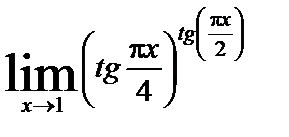
|
13. Методами дифференциального исчисления исследовать функции и построить их графики
| 13. 1 | 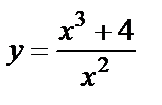
| 13. 2 | 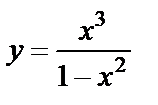
|
| 13. 3 | 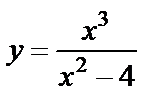
| 13. 4 | 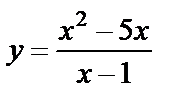
|
| 13. 5 | 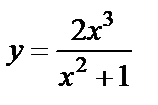
| 13. 6 | 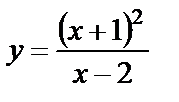
|
| 13. 7 | 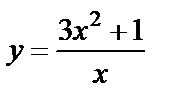
| 13. 8 | 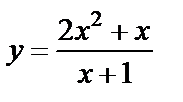
|
| 13. 9 | 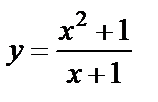
| 13. 10 | 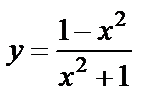
|
14. Найти наименьшее и наибольшее значения функции на отрезке
| 14. 1 | 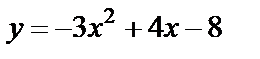 ; ; 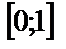
| 14. 2 | 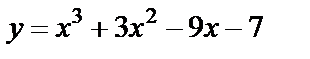 ; ; 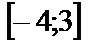
|
| 14. 3 | 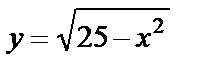 ; ; 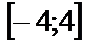
| 14. 4 | 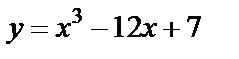 ; ; 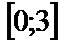
|
| 14. 5 | 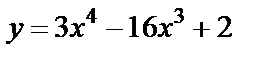 ; ; 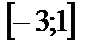
| 14. 6 | 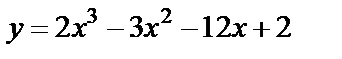 ; ; 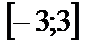
|
| 14. 7 | 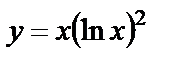 ; ; 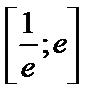
| 14. 8 | 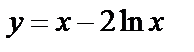 ; ; 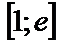
|
| 14. 9 | 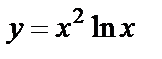 ; ; 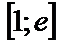
| 14. 10 | 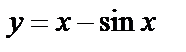 ; ; 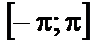
|
15. Найти частные производные 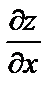 и
и 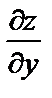 следующих функций
следующих функций
| 15. 1 | 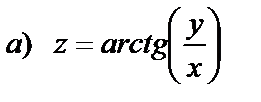
| 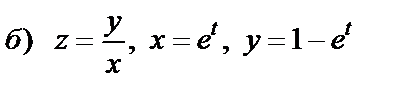
| 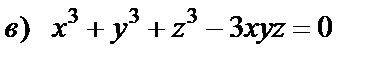
|
| 15. 2 | 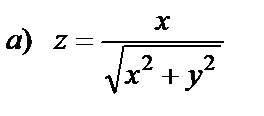
| 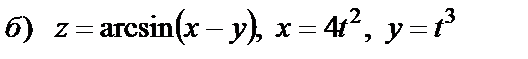
| 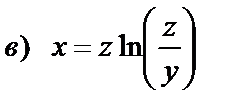
|
| 15. 3 | 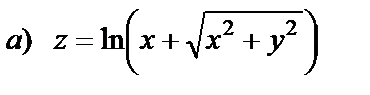
| 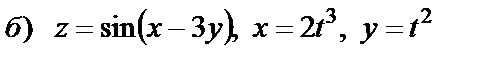
| 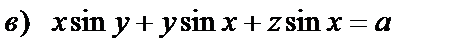
|
| 15. 4 | 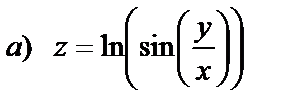
| 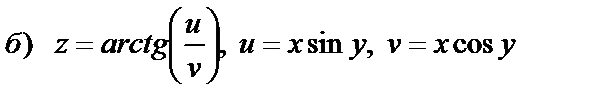
| 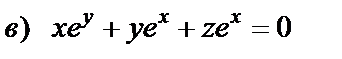
|
| 15. 5 | 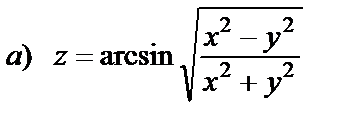
| 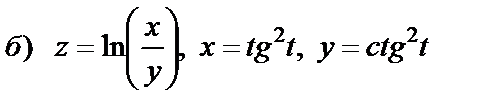
| 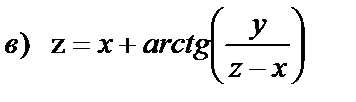
|
| 15. 6 | 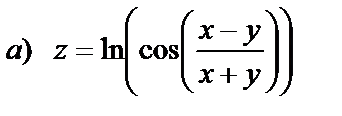
| 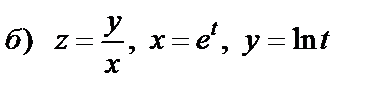
| 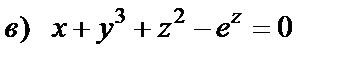
|
| 15. 7 | 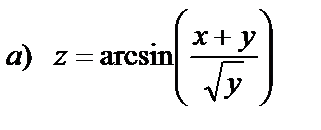
| 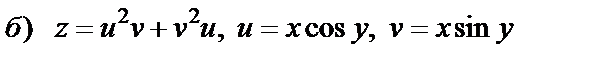
| 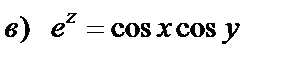
|
| 15. 8 | 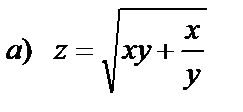
| 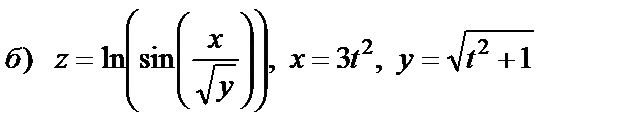
| 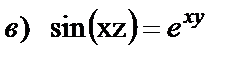
|
| 15. 9 | 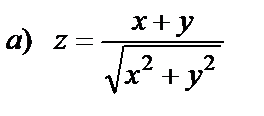
| 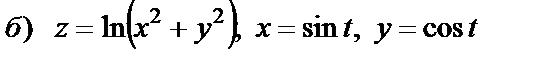
| 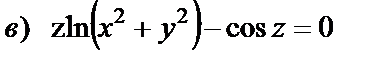
|
| 15. 10 | 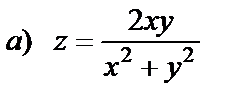
| 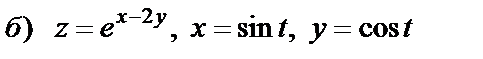
| 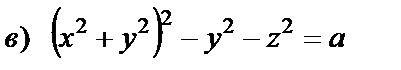
|
16. Найти полный дифференциал функции
| 16. 1 | 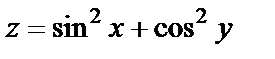
| 16. 2 | 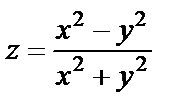
|
| 16. 3 | 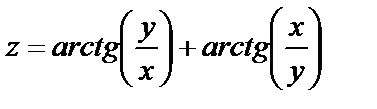
| 16. 4 | 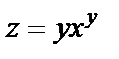
|
| 16. 5 | 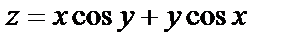
| 16. 6 | 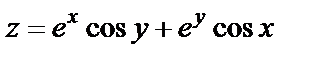
|
| 16. 7 | 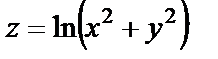
| 16. 8 | 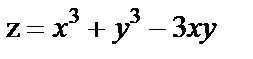
|
| 16. 9 | 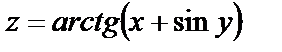
| 16. 10 | 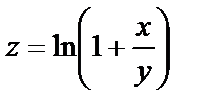
|
17. Проверить, удовлетворяет ли данная функция уравнению
| 17. 1 | 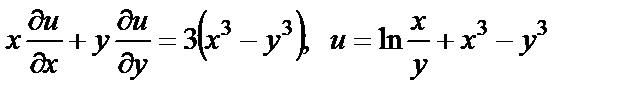
|
| 17. 2 | 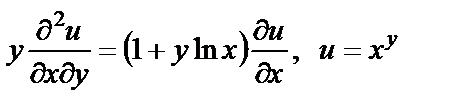
|
| 17. 3 | 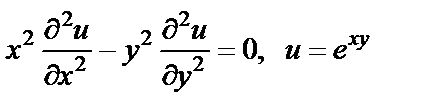
|
| 17. 4 | 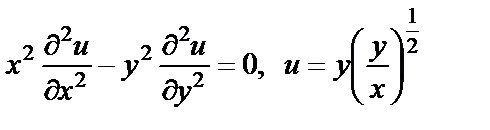
|
| 17. 5 | 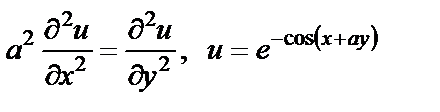
|
| 17. 6 | 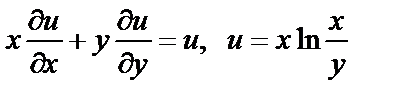
|
| 17. 7 | 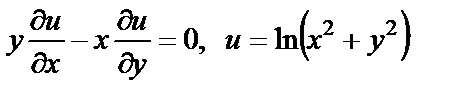
|
| 17. 8 | 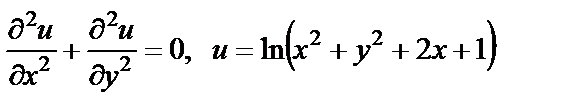
|
| 17. 9 | 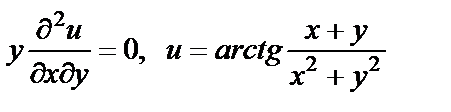
|
| 17. 10 | 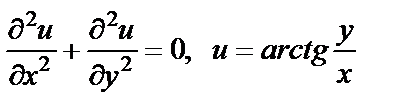
|
18. Исследовать на экстремум функции
| 18. 1 | 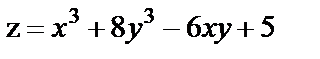
| 18. 2 | 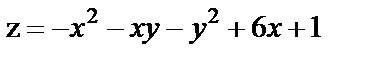
|
| 18. 3 | 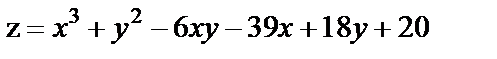
| 18. 4 | 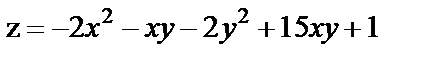
|
| 18. 5 | 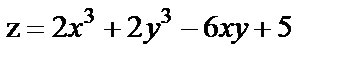
| 18. 6 | 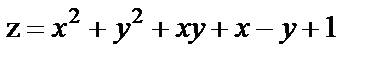
|
| 18. 7 | 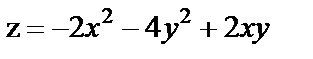
| 18. 8 | 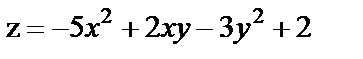
|
| 18. 9 | 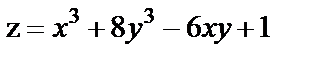
| 18. 10 | 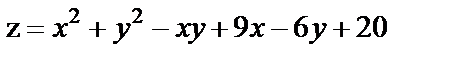
|
19. Найти наибольшее и наименьшее значения функции в области D, ограниченной данными линиями
| 19. 1 | 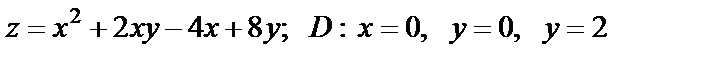
|
| 19. 2 | 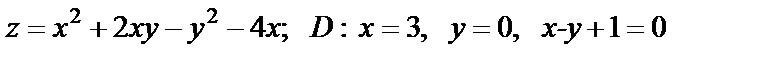
|
| 19. 3 | 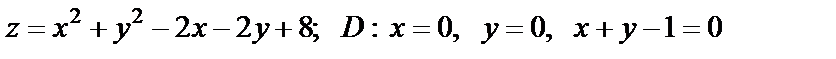
|
| 19. 4 | 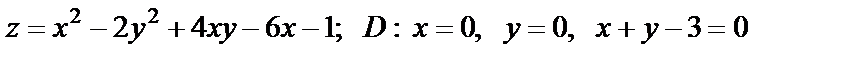
|
| 19. 5 | 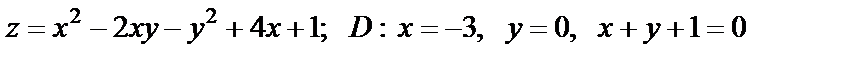
|
| 19. 6 | 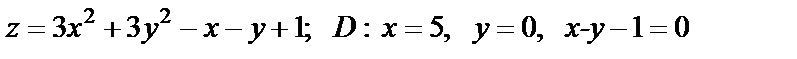
|
| 19. 7 | 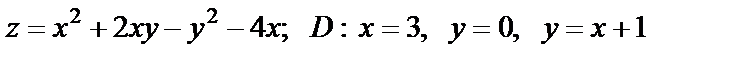
|
| 19. 8 | 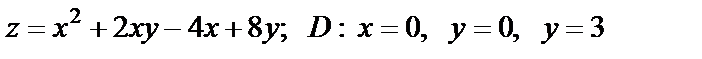
|
| 19. 9 | 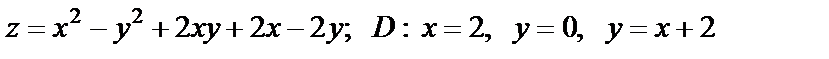
|
| 19. 10 | 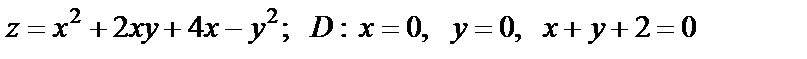
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|