Контрольная работа

Тема: «Параллельность прямых, прямой и плоскости, плоскостей».

I вариант.

1. Известно, что точки A, B, C, D лежат в одной плоскости. Определите, могут ли прямые AB и CD: а) быть параллельными; ; б) пересекаться в) быть скрещивающимися. 2. Через сторону AD четырехугольника ABCD проведена плоскость α. Известно, что Ð BCA = Ð CAD.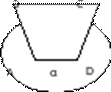

Докажите, что BC параллельно α. 3. Квадрат ABCD и трапеция BEFC не лежат в одной плоскости. Точки M и N середины отрезков BE и FC соответственно. а) докажите, что MN параллельно AD б) найдите MN, если AD=10 см, EF=6 см. 4. На стороне AD параллелограмма ABCD выбрана точка А1 так, что DA1=4 см. Плоскость, параллельная диагонали АС, проходит через точку А1 и пересекает сторону CD в точке С1.

а) Докажите подобие треугольников C1DA1 и ABC б) Найдите АС, если ВС=10 см, А1С1=6см. 5. Плоскость α пер

есекает стороны угла ВАС в точках А1 и В1, а параллельная ей плоскость β в точках А2 и В2. Найдите А2В2 и АА2, если А1В1=18, АА1=24, АА2=⅔ А1А2.

II вариант.

1. Известно, что точки A, B, C, D не лежат в одной плоскости. Определите, могут ли прямые AB и CD:

а) быть параллельными; б) пересекаться; в) быть скрещивающимися. 2. Через сторону AD четырехугольника ABCD проведена плоскость α. Известно, что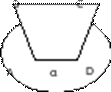

Ð ABC + Ð DAB = 180º . Докажите, что BC параллельно α. 3. Треугольник BEC и прямоугольник ABCD не лежат в одной плоскости. Точки M и N середины отрезков BE и EC соответственно. а) докажите, что AD параллельно MN б) найдите AD, если MN=5 см. 4. На стороне ВС параллелограмма ABCD выбрана точка С1 так, что С1В=3 см. Плоскость

пара ая диагонали АС, проходит через С1 и пересекает сторону АВ в точке А1. а) Докажите подобие треугольников ADС и C1ВA1 б) Найдите АD, если А1С1=4 см, АС=12см. 5. Плоскость α пересекает стороны угла ВАС в точках А1 и В1, а параллельная ей плоскость β в точках А2 и В2. Найдите АА2 и АВ2, если А1А2=2, А1А=12, АВ1=5.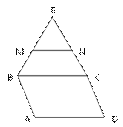

Решение писать в тетрадях, варианты выполнять по списку: нечетные – 1 вариант, четные 2 вариант. Работы всем сдать 17. 02. 2022 до 16-00