
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Теоретический материал для самостоятельного изучения
На прошлых уроках мы научились сравнивать, складывать и вычитать обыкновенные дроби.
Итак, обыкновенные дроби бывают правильными, когда числитель меньше знаменателя и неправильными, когда числитель больше или равен знаменателю.
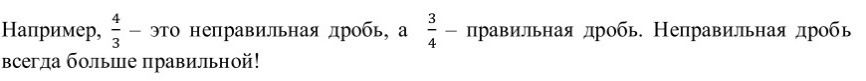
Давайте вспомним, как сравнить две дроби с общим знаменателем?
Чтобы сравнить две дроби, нужно ответить на вопрос, равны ли знаменатели. Если да, то из двух дробей с общим знаменателем больше та дробь, у которой числитель больше. Если нет, то нужно привести дроби к общему знаменателю, а затем сравнить числители.

А чтобы сложить дроби с разными знаменателями, их приводят к общему знаменателю двумя способами:
1. если знаменатели – взаимно простые числа, используем формулу:

2. в противном случае – находим наименьший общий знаменатель и используем формулу:

Например, сложение дробей с разными знаменателями:

Рассмотрим пример сложения дробей с одинаковыми знаменателями:

Правила вычитания очень похожи на правила сложения: чтобы вычесть две дроби, нужно определить, равные или разные у них знаменатели. А затем использовать то правило вычитания дробей, которое подходит в данном случае.
Вычитание обыкновенных дробей
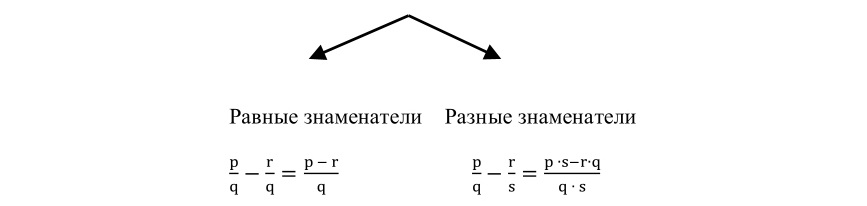
Например, вычитание дробей с разными знаменателями:

Вычитание дробей с равными знаменателями:

Итак, мы повторили основные правила на сравнение, сложение и вычитание обыкновенных дробей.
Разбор решения заданий тренировочного модуля

Решение: сначала приведём дроби к общему знаменателю, а затем найдём их разность:
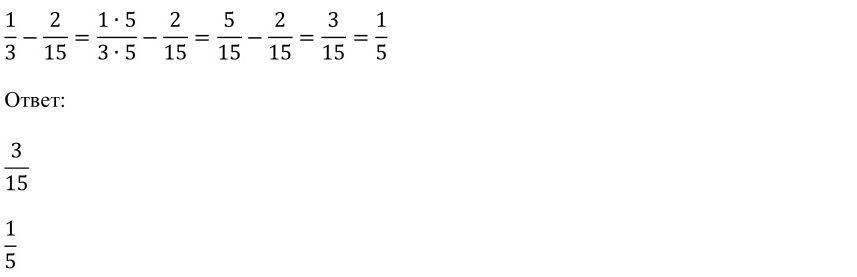
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|