
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Виды взаимодействий
Лекция №5. Второй закон Ньютона. Принцип суперпозиции сил. Третий закон Ньютона. Принцип относительности Галилея
План
1. Динамика материальной точки и поступательного движения твёрдого тела.
2. Виды взаимодействий.
3. Первый закон Ньютона.
4. Второй закон Ньютона.
5. Третий закон Ньютона.
6. Принцип относительности Галилея.
Динамика материальной точки и поступательного движения твёрдого тела
Динамика – раздел механики, изучающий движение тел с учетом причин, вызывающих это движение.
Основные понятия динамики
1. Масса (m) – скалярная физическая величина, являющаяся мерой инертных и гравитационных свойств тела. Может служить мерой энергосодержания.
[m] = кг.
Основные свойства массы:
- масса в классической механике не зависит от скорости движения;
- масса является величиной аддитивной, т. е. масса системы тел равняется сумме масс тел, входящих в систему;
- масса замкнутой системы остается величиной постоянной, т. е. выполняется за- кон сохранения массы.
Плотность (r) – скалярная физическая величина, характеристика материала, численно равная массе единицы объема.
 r = m . (5. 1)
r = m . (5. 1)
V
[r] =
кг.
 м3 →
м3 →
2. Импульс тела ( p ) – векторная физическая величина, равная произведению
массы тела на его скорость. → →
p = mv . (5. 2)
 [ p] = кг × м .
[ p] = кг × м .
с
Направление импульса тела совпадает с направлением скорости.
→
3. Сила ( F ) – векторная физическая величина, являющаяся мерой механиче-
ского воздействия на тело других тел или полей. Сила характеризуется модулем
(численным значением), направлением действия, точкой приложения. Прямая, вдоль которой направлена сила, называется линией действия силы.
[F ] = Н (ньютон)
Вид формулы для расчёта силы зависит от природы взаимодействия.
Виды взаимодействий
1. Гравитационные взаимодействия. Закон всемирного тяготения.
Две материальные точки массами m1 и m2 притягиваются друг к дру- гу с силой прямо пропорциональной массам этих точек и обратно пропор- циональной квадрату расстояния между ними (рис. 5. 1).
 F = G m1 m2, (5. 3)
F = G m1 m2, (5. 3)

|
 1
1
m
| |
Н × м2
кг 2
r 2
 – гравитационная постоянная.
– гравитационная постоянная.
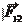
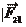

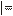
 F
F
Рисунок 5. 1
Если одно из взаимодействующих тел – Земля, а тело массой m находится на высоте h от поверхности Земли, то закон всемирного тяготения записывается в виде
где М – масса Земли;
R – средний радиус Земли.
F = G
M m
 |
(R + h)2,
На поверхности Земли (или вблизи поверхности) h » 0. В этом случае
 F = G M m .
F = G M m .
R 2
Можно ввести обозначение
G M = g ,
 R2
R2
где g – ускорение свободного падения. Величину
называют силой тяжести.
Fтяж = mg
(5. 4)
2. Электромагнитные взаимодействия.
Частными случаями проявления электромагнитных взаимодействий яв- ляются силы упругости и силы трения. Для этих сил можно получить лишь приближенные, т. е. основанные на опыте формулы.
а) Закон Гука.
Под действием внешних сил возникают деформации (т. е. изменение раз- меров и формы тел). Если после прекращения действия сил восстанавливаются прежняя форма и размеры тела, то деформация называется упругой.
Для упругих деформаций справедлив закон Гука:
Сила упругости пропорциональна абсолютному удлинению.
Fx = -k x , (5. 5)
где Fx – проекция силы упругости на ось х; k – жесткость пружины;
x – абсолютное удлинение пружины.
Для однородных стержней также справедлив закон Гука, который приня- то формулировать следующим образом:
Механическое напряжение прямо пропорционально относительному удлинению
Механическое напряжение:
s = Ee. (5. 6)
 s = F^ , (5. 7)
s = F^ , (5. 7)
S
где F^ – упругая сила, действующая перпендикулярно площади поперечного сечения стержня S.
Относительное удлинение:
где Dl – приращение длины;
l0 – первоначальная длина;
e = Dl , (5. 8)
 l0
l0
Е – модуль Юнга,
[E] = Н
 м2
м2
= Па.
Модуль Юнга (модуль упругих деформаций) – это физическая величина, характеризующая упругие свойства материала. Зависит от природы материала.
Посмотрите лекционную демонстрацию.
Закон Гука и нелинейные деформации.
http: //youtube. com/watch? v=sYjyAujrtmw
б) Закон сухого трения.


|


 N →
N →
 Fтр
Fтр
= m N
, (5. 9)
Рисунок 5. 2
где m – коэффициент трения скольжения. Он зависит от природы материалов и качества обработки соприкасаю-
щихся поверхностей. Значения коэффициентов трения определяют эксперимен- тальным путём.
Посмотрите лекционную демонстрацию.
Соскальзывание бруска с наклонной плоскости.
http: //youtube. com/watch? v=04gAToQ4r0U
в) Закон вязкого трения.
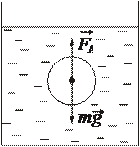 На тело, движущееся в вязкой (жидкой или газообразной) среде, действу- ет сила, тормозящая его движение. Эта сила называется си- лой вязкого трения
На тело, движущееся в вязкой (жидкой или газообразной) среде, действу- ет сила, тормозящая его движение. Эта сила называется си- лой вязкого трения
Рисунок 5. 3
F = -rv , (5. 10)
где v – скорость движения тела;
r – коэффициент сопротивления.
Коэффициент r зависит от формы и размеров тела, ха- рактера его поверхности, а также от свойств среды. Знак «–» указывает на то, что сила трения направлена противополож- но скорости.
г). Закон Архимеда.
На тело, погруженное в жидкость или газ, действует выталкиваю- щая сила, равная весу вытесненной телом жидкости или газа (рис. 5. 3)
где rж – плотность жидкости;
FA = rж gV , (5. 11)
V – объем погруженной части тела.
Основные законы динамики материальной точки (законы Ньютона)
Динамика базируется на законах Ньютона, которые математически не вы- водятся, а являются обобщением опыта.
Первый закон Ньютона
Первый закон Ньютона устанавливает факт существования инерциальных систем отсчёта и описывает характер движения свободной материальной точки в инерциальной системе отсчёта.
Всякое тело сохраняет состояние покоя или равномерного прямоли- нейного движения до тех пор, пока воздействия со стороны других тел не изменят этого состояния.
Свойство тел сохранять состояние покоя или равномерного прямолиней- ного движения называется инерцией . Система отсчёта, в которой выполняется первый закон Ньютона, называется инерциальной. Поэтому, первый закон Ньютона можно сформулировать и таким образом.
Существуют такие системы отсчёта, относительно которых тело находится в состоянии покоя или движется прямолинейно и равномерно, если на это тело не действуют другие тела или действие этих тел ском- пенсировано.
Любая другая система отсчёта, движущаяся относительно инерциальной с постоянной скоростью также является инерциальной.
Второй закон Ньютона
Скорость изменения импульса тела равна результирующей всех сил, действующих на тело :
→ dp→
Импульс тела равен ющим образом:
F =. (5. 12)
 dt
dt
p→ = mv→ . Формулу (6. 13) можно преобразовать следу-


|
dt dt dt
1. Уравнение (5. 13) можно применять как в тех случаях, когда масса ме- няется с течением времени (например, при полете ракеты), так и при изменении массы с изменением скорости.
2. Если масса тела остается постоянной ние (5. 13) примет следующий вид:
m = const, т. е.
dm = 0, то уравне-
 dt
dt
|
dv→

dt
= ma→ ,
|
Результирующая всех сил, действующих на тело, равна произведению массы тела на его ускорение.
3.
|
|
Проинтегрировав полученное уравнение, получим:
|
|
Импульс силы равен изменению импульса тела.
→ Dt ,
Из второго закона Ньютона следует, что изменения скоростей материаль- ных точек или тел происходят не мгновенно, а в течение конечных промежут- ков времени.
Посмотрите лекционные демонстрации.
1. Опыт с инерцией гири.
http: //youtube. com/watch? v=f7Aahv7_3Is
2. Выдергивание скатерти из-под сосуда с водой.
http: //youtube. com/watch? v=xVSWuvZ8aQA
Третий закон Ньютона
Силы, с которыми взаимодействуют два тела, равны по величине и противоположны по направлению.
→ = - →
. (5. 16)
F12 F21
Таким образом, силы всегда возникают попарно. Силы, фигурирующие в третьем законе Ньютона, приложены к разным телам, поэтому они не уравно- вешивают друг друга.
Законы Ньютона выполняются только в инерциальных системах отсчёта.
Посмотрите лекционные демонстрации.
1. Взаимодействие тележек. Два мотора.
http: //youtube. com/watch? v=bAp0pWg_iDI
2. Взаимодействие тележек. Один мотор.
http: //youtube. com/watch? v=exPXEi1wAcM
3. Взаимодействие тележек. Разные массы.
http: //youtube. com/watch? v=14LizsP4CGo
Закон сохранения импульса
Совокупность материальных точек (тел), выделенных для рассмотрения, называется механической системой. Силы, которые действуют на тела систе- мы, делят на внешние и внутренние. Внутренние силы обусловлены взаимо- действием тел, входящих в систему. Внешние силы обусловлены взаимодей- ствием с телами, не входящими в систему.
Система называется замкнутой, если на неё не действуют внешние силы.
Второй закон Ньютона, записанный для одного тела, можно применить и к системе тел. Если система является замкнутой (внешних сил нет), то из второ-
го закона Ньютона следует, что
dp→ = 0. (5. 17)
 dt
dt
Если производная некоторой величины равна нулю, то эта величина по-
стоянна. Поэтому из последнего уравнения следует, что p→ = const.
Импульс замкнутой системы материальных точек (тел) остается постоянным.
Закон сохранения импульса можно записать в развернутом виде:
| |
p→ 2 +
p→ 3 + × × × +
p→ n = const, (5. 18)
или
→ → → →
m1v1 + m2 v2 + m3v3 + × × × mnvn = const. (5. 19)
Закон сохранения импульса выполняется и для незамкнутых систем в следующих частных случаях.
1. На систему действуют внешние силы, но их векторная сумма равна ну-
лю.
2. Векторная сумма внешних сил не равна нулю, но равна нулю сумма
проекций этих сил на какое-либо направление, например, на направление оси x.
Полный импульс системы при этом не сохраняется, но сохраняется проекция
импульса на направление оси x.
2. Время действия сил очень мало. При этом изменение импульса
dp→
бу-
дет стремиться к нулю:
dp→ ® 0. В этом случае
p→ = const
- импульс системы со-
храняется. Примером является взаимодействие тел при ударе, взрыве.
Посмотрите лекционные демонстрации.
1. Выстрел назад с движущейся тележки.
http: //youtube. com/watch? v=HzHAj62yn5o
2. Выстрел вперёд с движущейся тележки.
http: //youtube. com/watch? v=-Hd8UEIFD0M
lS = V
- объём соленои-
Контрольные вопросы
1. Что называется материальной точкой?
2. Можно ли считать материальной точкой камень, брошенный вверх?
3. Как связано ускорение тела с силой?
4. Что такое инерция? Приведите примеры, демонстрирующие инерцию тел, не указанные в тексте.
5. В каких случаях направление скорости совпадает с направлением силы?
6. Можно ли утверждать, что первый закон Ньютона является следствием второго?
Литература

|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|