1 вариант:. Уровень А. 2 вариант

1 вариант:

Уровень А

1. В параллелограмме АВСD найдите:

а) стороны, если ВС на 8 см больше стороны АВ, а периметр равен 64 см;
б) углы, если угол А равен 38⁰.

2. В прямоугольной трапеции один угол 110⁰, найдите остальные углы.

3. Найдите одну из диагоналей ромба, если один из его углов 60⁰, а периметр равен 16 см.

Уровень В:

1. Дано: АВСD – прямоугольник, АВD = 48⁰. Найдите СОD, САD.

2. Периметр параллелограмма 46 см. Найдите стороны параллелограмма, если сумма трех его сторон равна 42 см.

3. Из вершины тупого угла ромба проведен перпендикуляр к его стороне, делящий эту сторону пополам. Найдите углы ромба.

Уровень С:

1. Дано: ABCD – параллелограмм, AD = 11 см, CD = 4 см. Периметр треугольника BOC равен 26 см. Найдите периметр треугольника АОВ, если точка О – точка пересечения диагоналей параллелограмма.

2. ABCD – прямоугольник (Рисунок4), BE ^ АС, АВ = 12 см, АЕ: ЕС = 1: 3. Найти диагонали прямоугольника.

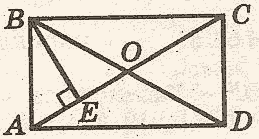
Рисунок 4.

3. В прямоугольной трапеции диагональ перпендикулярна к боковой стороне, острый угол трапеции равен 45⁰. Найдите отношение оснований.

2 вариант

Уровень А:

1. Один из углов параллелограмма в три раза больше другого его угла. Найдите все углы параллелограмма.

2. Докажите, что ромб, у которого угол между диагональю и стороной равен 45⁰, является квадратом.

3. В прямоугольнике ABCD диагонали пересекаются в точке О. Е – середина стороны АВ, ВАС = 50⁰. Чему равен ЕОD?

Уровень В:

1. ABCD – параллелограмм, ВЕ – биссектриса АВС; периметр ABCD равен 48 см, АЕ больше ED на 3 см. Найти стороны параллелограмма.

2. ABCD – прямоугольник; АОВ = 36⁰. Найти: CAD, BDC, если точка О – точка пересечения диагоналей прямоугольника.

3. Сторона ромба в два раза больше перпендикуляра, проведенного к ней из вершины тупого угла. Найдите углы ромба.

Уровень С:

1. Дано: ABCD – параллелограмм, точка О – точка пересечения диагоналей параллелограмма, периметр треугольника АОВ равен 21 см, периметр треугольника BOC 24 см, CD = 6 см. Найти периметр параллелограмма ABCD.

2. Дано: ABCD – прямоугольник (Рисунок5), СЕ BD, CD = 10 см, DЕ: ОС = 1: 2. Найти диагонали прямоугольника.

Рисунок 5.

3. В равнобедренной трапеции диагональ составляет с боковой стороной угол в 120⁰. Боковая сторона равна меньшему основанию. Найти углы трапеции.