03.04.2020 Тема урока «Решение неравенств с одной переменной»

Рекомендуем внимательно изучить видеоурок по ссылке https: //youtu. be/v4NgRLyMBpI

При изучении темы особое внимание уделите обозначениям промежутков, а также внимательно рассмотреть примеры решения и оформления решения неравенств с одной переменной.

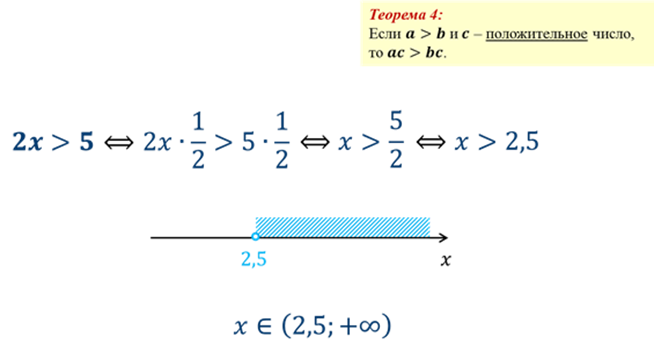
Ранее мы с вами изучили свойства числовых неравенств. На этом уроке нам понадобятся следующие теоремы:

Зная основные свойства числовых неравенств, и умея их правильно применять, можно научиться решать неравенства. Чем мы и будем заниматься на этом уроке.

Итак, рассмотрим неравенство:

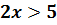
Такие неравенства называют неравенством с одной переменной или неравенством с одним неизвестным.

Но это не все решения данного неравенства. Чтобы найти все его решения, нужно рассмотреть следующие равносильные переходы.

Определение:

Решением неравенства с одной неизвестной называется значение переменной, которое обращает его в верное числовое неравенство.

Решить неравенство – это значит найти все его решения или доказать, что их нет.

Два неравенства называются равносильными, если каждое решение одного неравенства является решением другого, и наоборот, т. е. они имеют одни и те же решения. Равносильными называются и неравенства, которые не имеют решений.

Например:

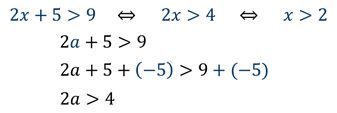
При решении неравенств используют следующие свойства:

Задание: решить неравенство:

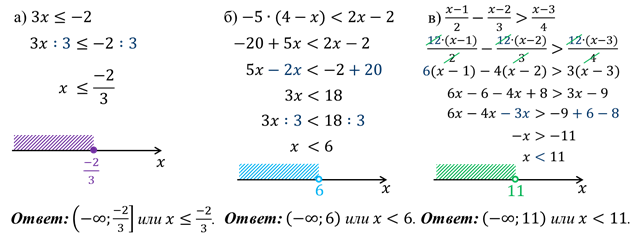
В каждом из рассмотренных примеров мы заменяли заданное неравенство равносильным ему неравенством вида 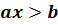или 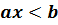, где а и b – некоторые числа.

Неравенства такого вида называют линейными неравенствами с одной переменной.

Обратите внимание, в примерах мы получали линейные неравенства, в которых коэффициент при переменной не равен нулю. Но может случиться так, что при решении неравенства мы придём к линейному неравенству вида 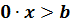или . Неравенство такого вида, а значит, и соответствующее исходное неравенство либо не имеют решений, либо их решением является любое число.

Например, решим неравенства:

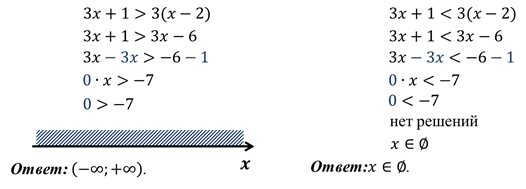
Итоги:

Неравенства вида 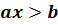, , 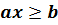, 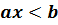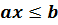называются линейными неравенствами с одной переменной.

Решить неравенство – это значит найти все его решения или доказать, что их нет.

Два неравенства называются равносильными, если каждое решение одного неравенства является решением другого.

Равносильными называются и неравенства, которые не имеют решений.

Домашнее задание

Изучить §11, п. 34, решить №835, №836.

Пройти тестирование по ссылке https: //testedu. ru/test/matematika/8-klass/neravenstva-s-odnoj-peremennoj-2. html

Выполненное домашнее задание и скриншот результатов тестирования прислать до 06. 04. 2020 на почту:

8-А licey12matem@mail. ru

8-Б gaika. guk51@gmail. com