
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Обработка опытных данных.
1. Тарировка расходомера
| δ | V, м. | t, с. | Q, м3/с |
Построить график зависимости Q от δ , для точности построения графика использовать метод наименьших квадратов для нахождения значений Q0 и A.
Q=Q0 + Aδ
для следующих лабораторных работ, если значение δ не совпадает с табличными данными использовать следующую формулу:

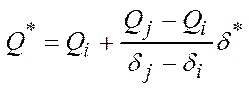
2. Потери напора в трубе круглого диаметра
| δ | Q, м3/с | h1, см | h2, см | hg, см | V, м/с | λ | Re | lgRe |
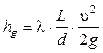
где hg -потери напора (полной механической энергии);
L и d - соответственно длина опытного участка трубы и ее диаметр;
υ - средняя скорость потока;
λ - гидравлический коэффициент трения.
По результатам измерений находятся следующие величины:
- потери напора по длине hg = h1 - h2;
- средняя скорость потока в трубе υ = 4Q / π d2;
- гидравлический коэффициент трения из формулы: λ = 2ghg d / Lυ 2;
- число Рейнольдса: Rе = υ d / ν 11
Построить график зависимости λ от числа Re. Также по значению λ и lgRe определить шероховатость трубы.
3. Уравнение Бернулли
| № точки | |||||||||||
| d, мм | |||||||||||
| S м2 | |||||||||||
| h, см | |||||||||||
| vср, м/с | |||||||||||
| Re | |||||||||||
| течение | |||||||||||
| α | |||||||||||
| α *v2/2g | |||||||||||
| Hпол. , м | |||||||||||
| hwi-j |
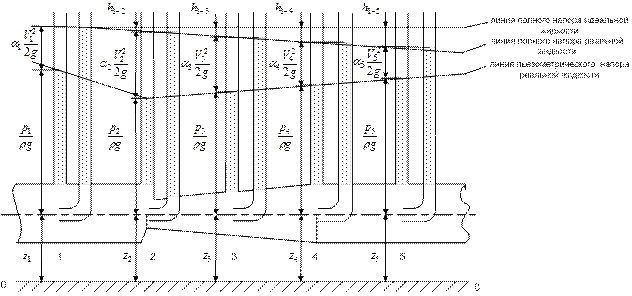 Рис. Схема к геометрическому изображению уравнения Бернулли
Рис. Схема к геометрическому изображению уравнения Бернулли
По результатам измерений следует вычислить скорость в каждом i -том сечении трубы Вентури:
υ i = Q/Si, а затем скоростной напор υ i2/2g
α тур. ≈ 1, 05
α лам. ≈ 2
ν =1, 032*10-6м2/с
H= h + α *v2/2g полный напор
На чертеж нанести:
- профиль трубы Вентури в масштабе;
- измеренные пьезометрические напоры для каждого i-того сечения:
откладывая их от оси трубы; вычертить пьезометрическую линию;
- скоростные напоры, суммируя их с ординатами пьезометрической линии в соответствующих сечениях; провести линию энергии;
- провести напорную плоскость (горизонтальную прямую) на уровне ординаты линии энергии первого пьезометра и обозначить потери напора (энергии) между этим сечением и любым, расположенным ниже по течению.
Рекомендуется провести 3 опыта с различными расходами для демонстрации изменения напоров в зависимости от расхода.
В заключение отчета о работе студента рекомендуется дать объяснения получившейся конфигурации пьезометрической линии и линии полного напора с точки напорное и энергетическое толкование.
4. Потери напора на внезапном расширении
| № опыта | δ | v/ м/с | Q, м3/с | ξ | h | ||||||||||||
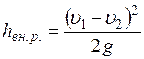 - потери напора на внезапном расширении
- потери напора на внезапном расширении
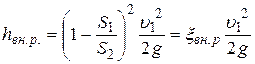
где S1 и S2 - площади нормальных сечений; ξ вн. р -коэффициент потерь на внезапном расширении.
h=h5 – h4
Обработка опытных данных.
При определении коэффициента местного сопротивления (в данном случае внезапного расширения) необходимо иметь в виду, что за местным сопротивлением, где поток претерпевает значительную деформацию лежит достаточно протяженный «участок стабилизации», на котором существуют, крупные вихри с возвратными течениями. Поэтому экспериментальный коэффициент местного сопротивления должен учитывать полные потери на участке стабилизации, а значит должен явно зависеть от числа Рейнольдса. Совпадение с теоретической формулой Борда можно ожидать только при весьма больших числах Рейнольдса.
Расчетными соотношениями для определения коэффициента местного сопротивления по экспериментальным данным являются следующие. Применительно к рисунку, из уравнения Бернулли для сечения 1 и 2 следует
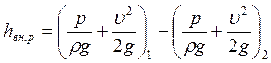
где hвн. р – искомые потери на внезапном расширении.
Здесь сечение 2 выбирается на расстоянии достаточном для расширения потока на все сечение S2. Отнеся потери к скоростному напору υ 12 / 2g, получим:
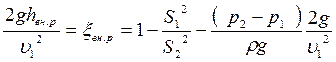
Разности пьезометрических напоров p2-p1 / pg определяется по пьезометрам 1 и 2, а скорость υ 1 по расходу, измеренному ротаметром. Тогда последняя формула позволяет вычислить экспериментальное значение ξ вн. р.
Измерив пьезометрами давления во всех точках их подключения, можно построить пьезометрическую линию вдоль трубы, а так же линию энергии. Студентам рекомендуется объяснить физическую сущность этих графиков, а также обозначить на них потери напора в местном сопротивлении.
В данной лабораторной работе следует построить график уравнения Бернулли, соотнесенную в масштабе с самой экспериментальной трубой. Также в рамках этой работы необходимо вычислить погрешность измерений:
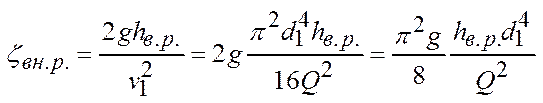
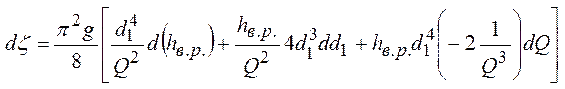
d(d1)=0, 01мм
d(hв. р. )=2мм
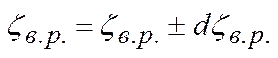
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|