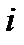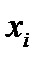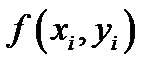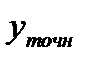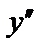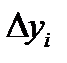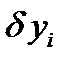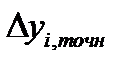- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа № 5.. Пример выполнения практической работы № 5.
Практическая работа № 5.
Задание 1. Используя метод Эйлера найти приближенные значения решения обыкновенного дифференциального уравнения 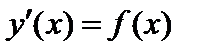 на отрезке
на отрезке 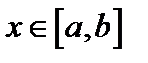 с шагом
с шагом 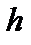 при начальном условии
при начальном условии 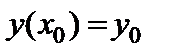 . Построить графики точного и численного решений.
. Построить графики точного и численного решений.
| Вариант | Дифферениальное уравнение первого порядка | Отрезок 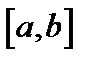
| Шаг 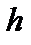
| Начальное условие 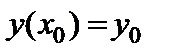
|
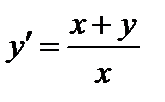
| 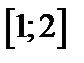
| 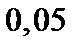
| 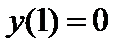
| |
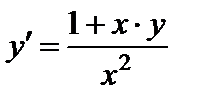
| 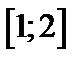
| 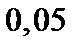
| 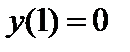
| |
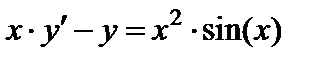
| 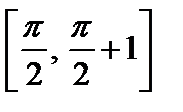
| 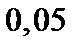
| 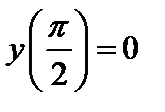
| |
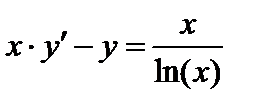
| 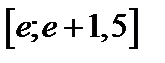
| 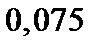
| 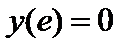
| |
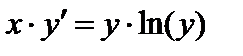
| 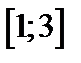
| 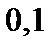
| 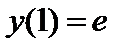
| |
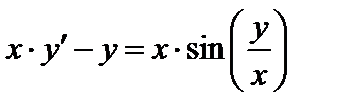
| 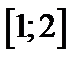
| 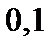
| 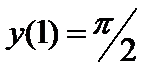
| |
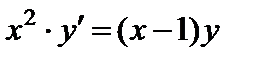
| 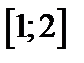
| 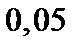
| 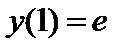
| |
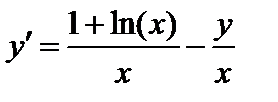
| 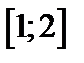
| 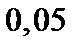
| 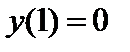
| |
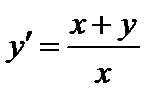
| 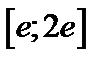
| 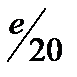
| 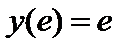
| |
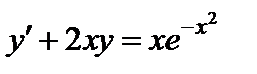
| 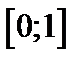
| 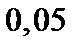
| 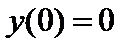
| |
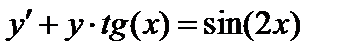
| 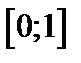
| 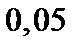
| 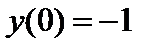
| |
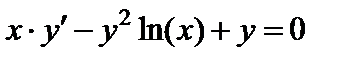
| 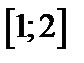
| 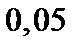
| 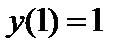
| |
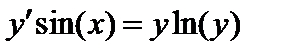
| 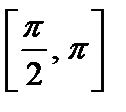
| 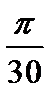
| 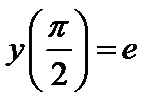
| |
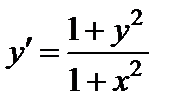
| 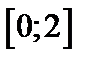
| 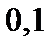
| 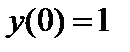
| |
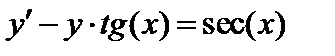
| 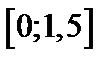
| 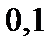
| 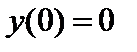
| |
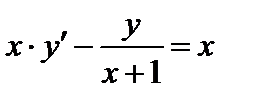
| 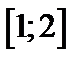
| 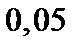
| 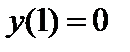
| |
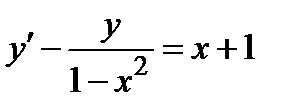
| 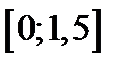
| 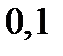
| 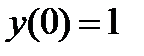
| |
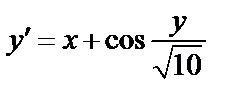
| 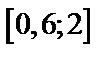
| 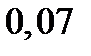
| 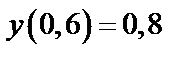
| |
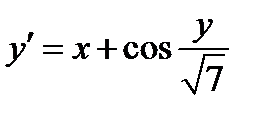
| 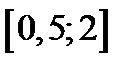
| 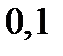
| 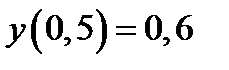
| |
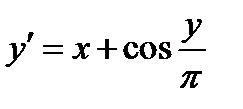
| 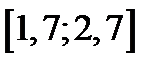
| 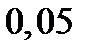
| 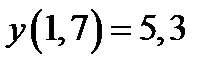
|
Задание 2. Используя метод Рунге-Кутта найти приближенные значения решения обыкновенного дифференциального уравнения 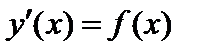 на отрезке
на отрезке 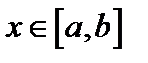 с шагом
с шагом 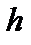 при начальном условии
при начальном условии 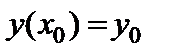 . Построить графики точного и численного решений.
. Построить графики точного и численного решений.
| Вариант | Дифферениальное уравнение первого порядка | Отрезок 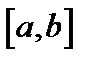
| Шаг 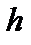
| Начальное условие 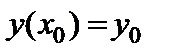
|
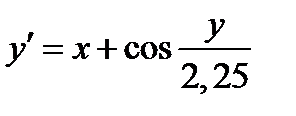
| 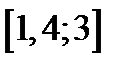
| 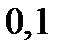
| 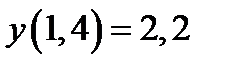
| |
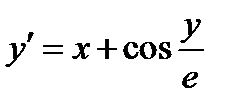
| 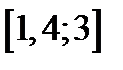
| 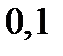
| 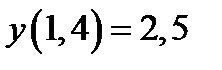
| |
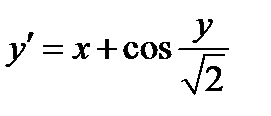
| 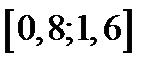
| 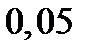
| 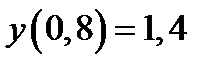
| |
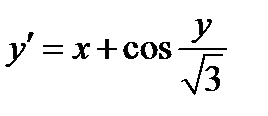
| 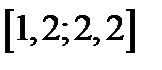
| 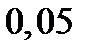
| 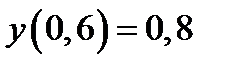
| |
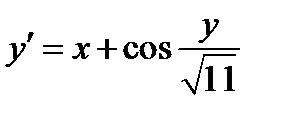
| 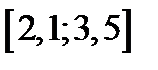
| 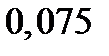
| 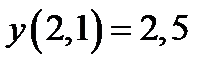
| |
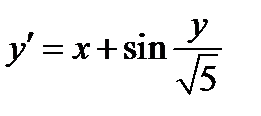
| 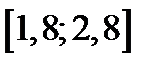
| 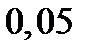
| 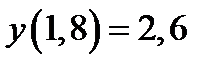
| |
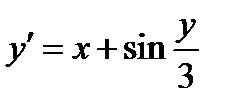
| 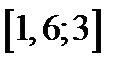
| 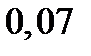
| 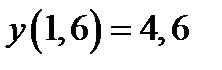
| |
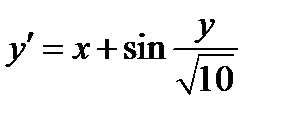
| 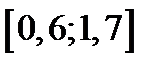
| 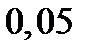
| 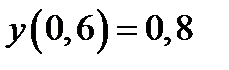
| |
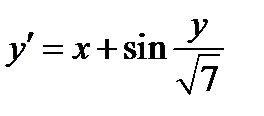
| 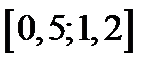
| 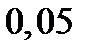
| 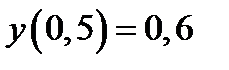
| |
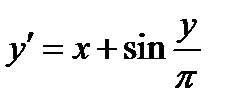
| 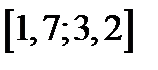
| 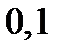
| 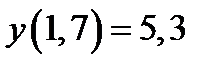
| |
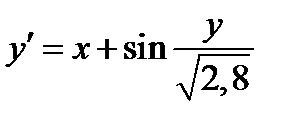
| 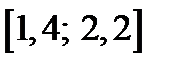
| 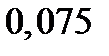
| 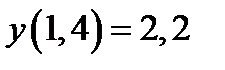
| |
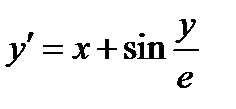
| 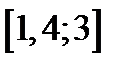
| 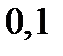
| 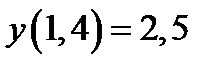
| |
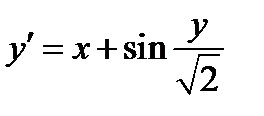
| 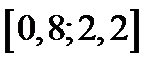
| 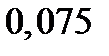
| 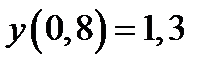
| |
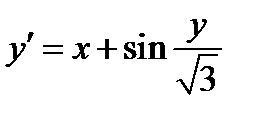
| 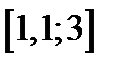
| 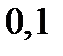
| 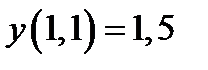
| |
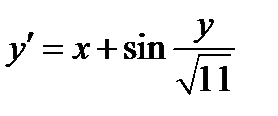
| 
| 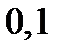
| 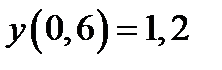
| |
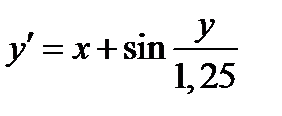
| 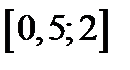
| 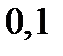
| 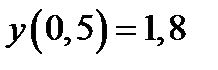
| |
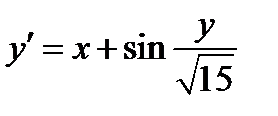
| 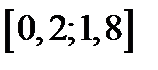
| 
| 
| |
| 
| 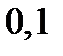
| 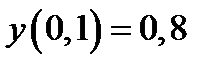
| |
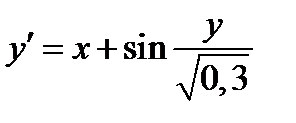
| 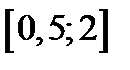
| 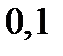
| 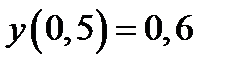
| |
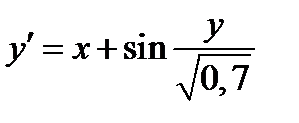
| 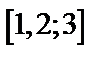
| 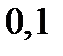
| 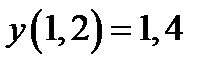
|
Пример выполнения практической работы № 5.
Задание 1. Найти приближенное решение дифференциального уравнения первого порядка методом Эйлера с шагом 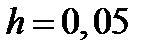 :
:
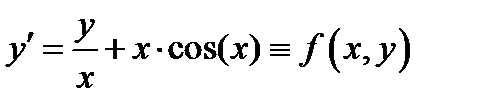 ,
, 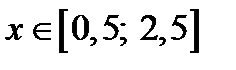 ,
, 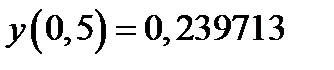 .
.
Решение:
Составим вспомогательную таблицу значений
|
|
|
|
|
|
|
| 0, 5 | 0, 918217 | 0, 239713 | 0, 239713 | 1, 515452 | |
| 0, 55 | 0, 988204 | 0, 285624 | 0, 287478 | 1, 417571 | |
| 0, 6 | 1, 053591 | 0, 335034 | 0, 338785 | 1, 311886 | |
| 0, 65 | 1, 113937 | 0, 387713 | 0, 393371 | 1, 198796 | |
| 0, 7 | 1, 168833 | 0, 44341 | 0, 450952 | 1, 078732 | |
| 0, 75 | 1, 217902 | 0, 501852 | 0, 511229 | 0, 952149 | |
| 0, 8 | 1, 260799 | 0, 562747 | 0, 573885 | 0, 819529 | |
| 0, 85 | 1, 297206 | 0, 625787 | 0, 638588 | 0, 681378 | |
| 0, 9 | 1, 326835 | 0, 690647 | 0, 704994 | 0, 538226 | |
| 0, 95 | 1, 349429 | 0, 756989 | 0, 772745 | 0, 390621 | |
| 1, 364763 | 0, 82446 | 0, 841471 | 0, 239134 | ||
| 1, 05 | 1, 372639 | 0, 892699 | 0, 910794 | 0, 084348 | |
| 1, 1 | 1, 372893 | 0, 96133 | 0, 980328 | 0, 073136 | |
| 1, 15 | 1, 365391 | 1, 029975 | 1, 049679 | 0, 232704 | |
| 1, 2 | 1, 350033 | 1, 098245 | 1, 118447 | 0, 393731 | |
| 1, 25 | 1, 32675 | 1, 165746 | 1, 186231 | 0, 555586 | |
| 1, 3 | 1, 295505 | 1, 232084 | 1, 252626 | 0, 717628 | |
| 1, 35 | 1, 256295 | 1, 296859 | 1, 317227 | 0, 879213 | |
| 1, 4 | 1, 20915 | 1, 359674 | 1, 37963 | 1, 039695 | |
| 1, 45 | 1, 15413 | 1, 420131 | 1, 439434 | 1, 198428 | |
| 1, 5 | 1, 091331 | 1, 477838 | 1, 496242 | 1, 354768 | |
| 1, 55 | 1, 02088 | 1, 532404 | 1, 549665 | 1, 508075 | |
| 1, 6 | 0, 942936 | 1, 583448 | 1, 599318 | 1, 657717 | |
| 1, 65 | 0, 85769 | 1, 630595 | 1, 644827 | 1, 803069 | |
| 1, 7 | 0, 765364 | 1, 67348 | 1, 68583 | 1, 943519 | |
| 1, 75 | 0, 666211 | 1, 711748 | 1, 721975 | 2, 078468 | |
| 1, 8 | 0, 560513 | 1, 745058 | 1, 752926 | 2, 207330 | |
| 1, 85 | 0, 448582 | 1, 773084 | 1, 778359 | 2, 329540 | |
| 1, 9 | 0, 330757 | 1, 795513 | 1, 79797 | 2, 444549 | |
| 1, 95 | 0, 207404 | 1, 812051 | 1, 811471 | 2, 551833 | |
| 0, 078917 | 1, 822421 | 1, 818595 | 2, 650889 | ||
| 2, 05 | -0, 05429 | 1, 826367 | 1, 819093 | 2, 741238 | |
| 2, 1 | -0, 19177 | 1, 823653 | 1, 81274 | 2, 822432 | |
| 2, 15 | -0, 33307 | 1, 814064 | 1, 799332 | 2, 894048 | |
| 2, 2 | -0, 4777 | 1, 797411 | 1, 778692 | 2, 955694 | |
| 2, 25 | -0, 62516 | 1, 773526 | 1, 750665 | 3, 007012 | |
| 2, 3 | -0, 77493 | 1, 742268 | 1, 715122 | 3, 047674 | |
| 2, 35 | -0, 92647 | 1, 703522 | 1, 671962 | 3, 077389 | |
| 2, 4 | -1, 07925 | 1, 657198 | 1, 621112 | 3, 095899 | |
| 2, 45 | -1, 23268 | 1, 603236 | 1, 562524 | 3, 102986 | |
| 2, 5 | -1, 38622 | 1, 541601 | 1, 49618 | 3, 098468 |
|
|
|
|
|
|
|
| 0, 5 |
|
|
|
| |
| 0, 55 | 0, 001894 | 0, 66% | 0, 00185 | 0, 65% | |
| 0, 6 | 0, 003666 | 1, 08% | 0, 00375 | 1, 11% | |
| 0, 65 | 0, 005306 | 1, 35% | 0, 00566 | 1, 44% | |
| 0, 7 | 0, 006805 | 1, 51% | 0, 00754 | 1, 67% | |
| 0, 75 | 0, 008153 | 1, 59% | 0, 00938 | 1, 83% | |
| 0, 8 | 0, 009343 | 1, 63% | 0, 01114 | 1, 94% | |
| 0, 85 | 0, 010368 | 1, 62% | 0, 01280 | 2, 00% | |
| 0, 9 | 0, 011219 | 1, 59% | 0, 01435 | 2, 04% | |
| 0, 95 | 0, 011892 | 1, 54% | 0, 01576 | 2, 04% | |
| 0, 012380 | 1, 47% | 0, 01701 | 2, 02% | ||
| 1, 05 | 0, 012679 | 1, 39% | 0, 01810 | 1, 99% | |
| 1, 1 | 0, 012785 | 1, 30% | 0, 01900 | 1, 94% | |
| 1, 15 | 0, 013076 | 1, 25% | 0, 01970 | 1, 88% | |
| 1, 2 | 0, 013568 | 1, 21% | 0, 02020 | 1, 81% | |
| 1, 25 | 0, 014262 | 1, 20% | 0, 02048 | 1, 73% | |
| 1, 3 | 0, 015159 | 1, 21% | 0, 02054 | 1, 64% | |
| 1, 35 | 0, 016258 | 1, 23% | 0, 02037 | 1, 55% | |
| 1, 4 | 0, 017558 | 1, 27% | 0, 01996 | 1, 45% | |
| 1, 45 | 0, 019056 | 1, 32% | 0, 01930 | 1, 34% | |
| 1, 5 | 0, 020749 | 1, 39% | 0, 01840 | 1, 23% | |
| 1, 55 | 0, 022635 | 1, 46% | 0, 01726 | 1, 11% | |
| 1, 6 | 0, 024707 | 1, 54% | 0, 01587 | 0, 99% | |
| 1, 65 | 0, 026961 | 1, 64% | 0, 01423 | 0, 87% | |
| 1, 7 | 0, 029390 | 1, 74% | 0, 01235 | 0, 73% | |
| 1, 75 | 0, 031988 | 1, 86% | 0, 01023 | 0, 59% | |
| 1, 8 | 0, 034747 | 1, 98% | 0, 00787 | 0, 45% | |
| 1, 85 | 0, 037659 | 2, 12% | 0, 00528 | 0, 30% | |
| 1, 9 | 0, 040715 | 2, 26% | 0, 00246 | 0, 14% | |
| 1, 95 | 0, 043905 | 2, 42% | 0, 00058 | 0, 03% | |
| 0, 047218 | 2, 60% | 0, 00383 | 0, 21% | ||
| 2, 05 | 0, 050645 | 2, 78% | 0, 00727 | 0, 40% | |
| 2, 1 | 0, 054173 | 2, 99% | 0, 01091 | 0, 60% | |
| 2, 15 | 0, 057790 | 3, 21% | 0, 01473 | 0, 82% | |
| 2, 2 | 0, 061485 | 3, 46% | 0, 01872 | 1, 05% | |
| 2, 25 | 0, 065244 | 3, 73% | 0, 02286 | 1, 31% | |
| 2, 3 | 0, 069053 | 4, 03% | 0, 02715 | 1, 58% | |
| 2, 35 | 0, 072900 | 4, 36% | 0, 03156 | 1, 89% | |
| 2, 4 | 0, 076770 | 4, 74% | 0, 03609 | 2, 23% | |
| 2, 45 | 0, 080649 | 5, 16% | 0, 04071 | 2, 61% | |
| 2, 5 | 0, 084527 | 5, 65% | 0, 04542 | 3, 04% |
где 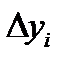 -абсолютная погрешность нахождения
-абсолютная погрешность нахождения 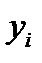 определяемая следующим образом:
определяемая следующим образом: 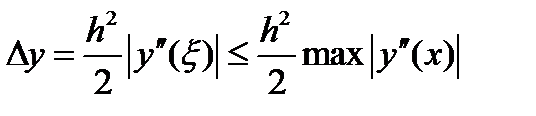 ,
, 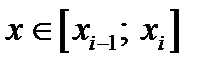 .
.
Построим графики точных и приближенных значений функции 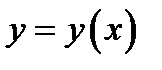 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|