
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Иррациональные неравенства
IV. Иррациональные неравенства
Неравенства называются иррациональными, если его неизвестное входит
под знак корня (радикала).
Иррациональное неравенство вида 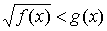 равносильно системе неравенств:
равносильно системе неравенств:
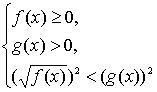
Иррациональное неравенство вида 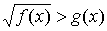
равносильно совокуп-ности двух систем неравенств:
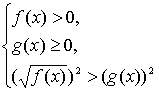 и
и 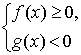
Решение иррациональных неравенств стандартного вида:
а) Решить неравенство 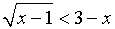
Решение.
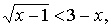
Данное неравенство равносильно системе неравенств:
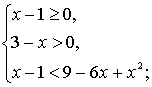
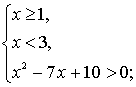
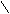
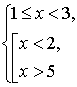

+ – +

1 3 x
Ответ: [1; 2).
б) Решить неравенство 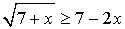
Решение.
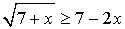
Данное неравенство равносильно двум системам неравенств:
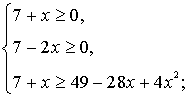
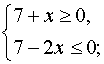
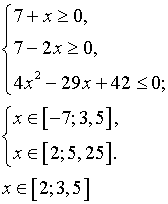
Ответ: 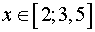
в) Решить неравенство 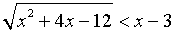
Решение.
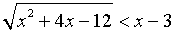
Данное неравенство равносильно системе неравенств:
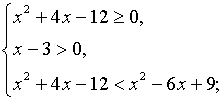
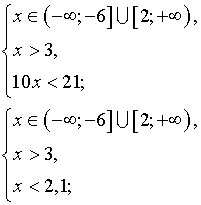
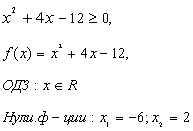
Ответ: нет решений 
Решение иррациональных неравенств нестандартного вида:
а) Решить неравенство 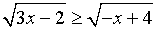
Решение.
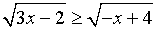
Данное неравенство равносильно системе неравенств:
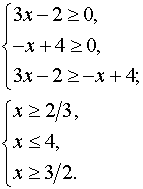
Ответ: 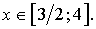
б) Решить неравенство 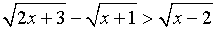
Решение.
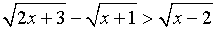
Данное неравенство равносильно системе неравенств:
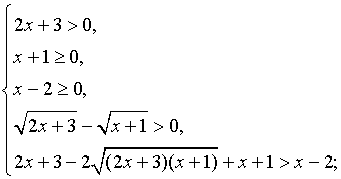
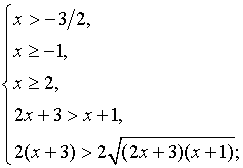
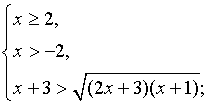
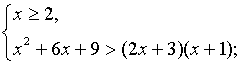
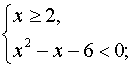
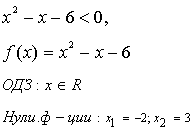
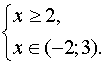
Ответ: 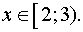
·
Решение иррациональных неравенств с помощью правила знаков
при умножении и делении :
а) Решить неравенство 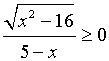
Решение.
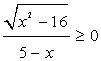
Учитывая то, что 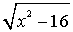
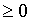
и правило знаков при делении данное неравенство равносильно системе
неравенств:
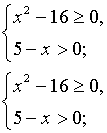
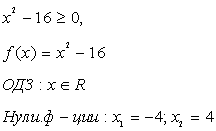
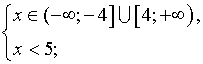
Ответ: 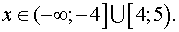
б) Решить неравенство (2x – 5) 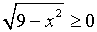
Решение.
(2x – 5) 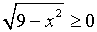
Учитывая то, что 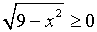 и
и
правило знаков при делении данное неравенство равносильно системе
неравенств:
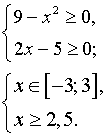
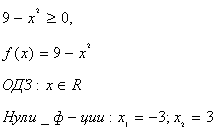
Ответ: 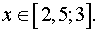
·
Решение иррациональных неравенств способом группировки:
Решить неравенство 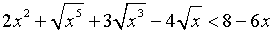
Решение.
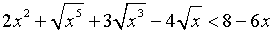 ,
,
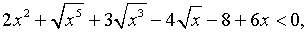 сгруппируем по два слагаемых
сгруппируем по два слагаемых
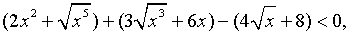
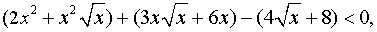
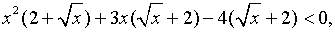 вынесем общий множитель за скобку
вынесем общий множитель за скобку 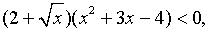 учитывая, что
учитывая, что 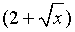 > 0
> 0
и правило знаков при умножении данное неравенство равносильно системе неравенств: 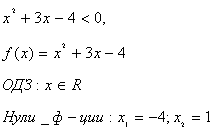
Ответ: 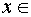 ( 0; 1 )
( 0; 1 )
Иррациональное неравенство, содержащее два знака иррациональности:
Решить неравенство 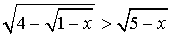
Решение.
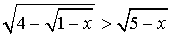
Данное неравенство равносильно системе неравенств:
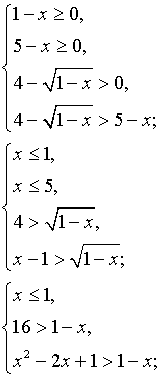
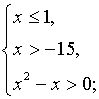
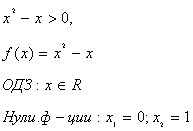
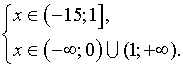
Ответ: 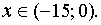
Решение иррациональных неравенств заменой:
Решить неравенство 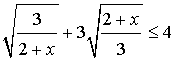
Решение.
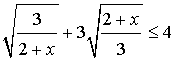
Пусть 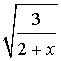 = t, тогда
= t, тогда 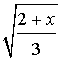 =
= 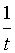 , t > 0
, t > 0
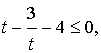
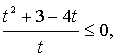
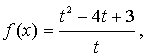
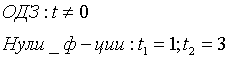
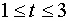
Сделаем обратную замену:
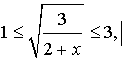 возведем в квадрат обе части неравенства
возведем в квадрат обе части неравенства
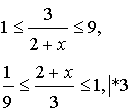
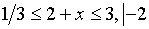
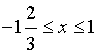
Ответ: 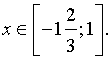
Решение иррациональных неравенств смешанного вида:
Иррациональные показательные неравенства:
а) Решить неравенство 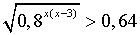
Решение.
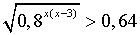 ,
,
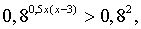 т. к. y = 0, 8t
т. к. y = 0, 8t 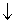 , то
, то
0, 5x(x – 3) < 2,
0, 5x2 – 1, 5x – 2 < 0,
x2 – 3x – 4 < 0,
f(x) = x2 – 3x – 4,
ОДЗ 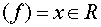 ,
,
+ – +

Нули функции: x1 = 4; x2 = – 1.
–1 4 x
Ответ: х 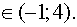
б) Решить неравенство 4 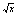 – 2
– 2 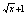 < 2
< 2 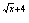 – 32
– 32
Решение.
4 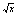 – 2
– 2 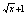 < 2
< 2 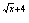 – 32, ОДЗ: x > 0
– 32, ОДЗ: x > 0
2 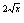 – 2
– 2 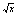
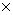 2 < 2
2 < 2 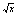
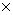 24 – 25, выполним группировку слагаемых
24 – 25, выполним группировку слагаемых
2 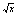 (2
(2 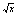 – 2) – 24(2
– 2) – 24(2 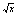 –2) < 0,
–2) < 0,
(2 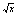 – 2)
– 2) 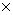
(2 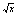 – 24)
– 24)
< 0, учитывая правило знаков и ОДЗ данное неравенство равносильно 2-м
системам:
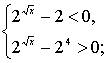 или
или 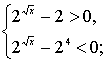

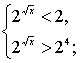 т. к. y = 2t
т. к. y = 2t  , то
, то 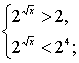 т. к. y = 2t
т. к. y = 2t 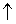 , то
, то
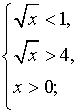
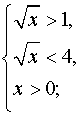
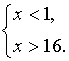
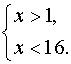
Ответ: х
Решение иррациональных логарифмических неравенств:
Решить неравенство 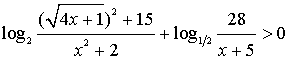
Решение.
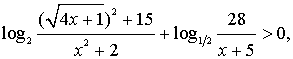 уч. ОДЗ данное нер-во равносильно системе нер-ств
уч. ОДЗ данное нер-во равносильно системе нер-ств
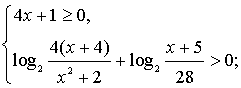
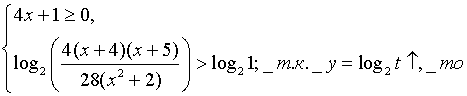
Иррациональные неравенства
Если в неравенство входят функции под знаком корня, то такие неравенства называют иррациональными.
Стандартный метод решения этих неравенств заключается в возведении обеих частей неравенства в нужную степень: если в неравенство входит квадратный корень, то в квадрат; входит корень третьей степени − в куб и т. д. Однако, как было показано выше в правиле 4 преобразования неравенств, возводить в квадрат, не нарушая равносильности, можно только неравенство, у которого обе части неотрицательны. При возведении же в квадрат неравенств, части которых имеют разные знаки, могут получиться неравенства, как равносильные исходному, так и неравносильные ему. Простой пример: –1 < 3 − верное неравенство, 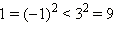 − тоже верное неравенство. Несмотря на то, что –4 < –1 − неравенство верное, неравенство
− тоже верное неравенство. Несмотря на то, что –4 < –1 − неравенство верное, неравенство 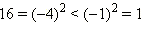 уже верным не является.
уже верным не является.
Покажем, как получить равносильные системы для некоторых часто встречающихся типов неравенств.
Неравенства вида 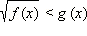
Если x лежит в ОДЗ: f ( x ) ≥ 0, то левая часть неравенства существует и неотрицательна. Поскольку для всех x, являющихся решением данного неравенства, правая часть больше левой, то g ( x ) > 0. Следовательно, обе части неравенства неотрицательны (для тех x, которые являются решениями неравенства, другие x нас не интересуют). Значит, возведение в квадрат не нарушает равносильности и можно записать равносильную нашему неравенству систему неравенств:
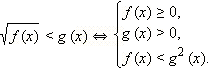
Пример 1
Решите неравенство 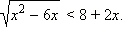
Сразу перейдём к равносильной системе:
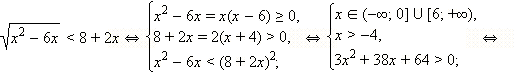
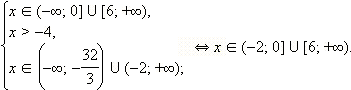
Ответ. 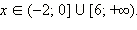
Пример 2
Решите неравенство 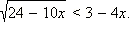
Перейдём к равносильной системе:
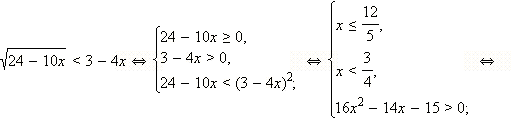
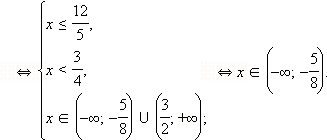
Ответ. 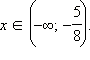
Неравенства вида 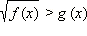
ОДЗ данного неравенства f ( x ) ≥ 0. Пусть для каких-то x из ОДЗ g ( x ) < 0. Тогда, очевидно, все эти x − решения, так как при этих x левая часть определена ( x 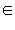 ОДЗ) и неотрицательна, в то время как правая часть g ( x ) < 0.
ОДЗ) и неотрицательна, в то время как правая часть g ( x ) < 0.
Для других x из ОДЗ g ( x ) ≥ 0. Для них обе части неравенства неотрицательны, и его можно возвести в квадрат: 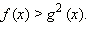 Значит, данное неравенство равносильно совокупности неравенств:
Значит, данное неравенство равносильно совокупности неравенств:
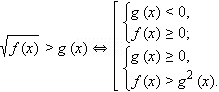
Заметим, что в последнюю систему не входит требование f ( x ) ≥ 0. Оно и не нужно, так как выполняется автоматически 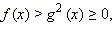 ибо полный квадрат всегда неотрицателен.
ибо полный квадрат всегда неотрицателен.
Пример 3
Решите неравенство 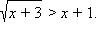
ОДЗ неравенства: x ≥ –3.
1. Если 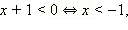 то все эти x
то все эти x 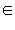 ОДЗ, для которых верно x < –1, − решения. Таким образом,
ОДЗ, для которых верно x < –1, − решения. Таким образом, 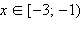 − первая часть ответа.
− первая часть ответа.
2. Если 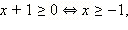 то обе части неравенства неотрицательны, и его можно возвести в квадрат. Имеем:
то обе части неравенства неотрицательны, и его можно возвести в квадрат. Имеем:
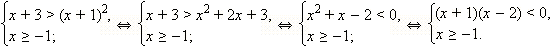
Получаем, что решениями являются все 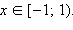
Объединяя результаты пунктов 1 и 2, получаем:
Ответ. 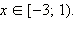
Пример 4
Решите неравенство 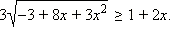
ОДЗ данного неравенства: 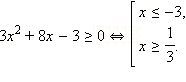 Будем рассматривать только эти x, другие x не могут являться решениями данного неравенства.
Будем рассматривать только эти x, другие x не могут являться решениями данного неравенства.
1. Если 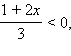 то есть
то есть 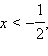 то все такие x из ОДЗ, удовлетворяющие этому условию, являются решениями неравенства. Значит, все x ≤ –3 − решения неравенства.
то все такие x из ОДЗ, удовлетворяющие этому условию, являются решениями неравенства. Значит, все x ≤ –3 − решения неравенства.
2. Если 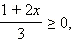 то есть
то есть 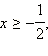 а с учетом ОДЗ это означает, что
а с учетом ОДЗ это означает, что 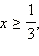 то обе части неравенства неотрицательны. Возведём обе части неравенства в квадрат:
то обе части неравенства неотрицательны. Возведём обе части неравенства в квадрат:
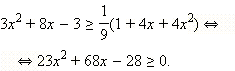
Уравнение 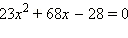 имеет корни
имеет корни 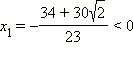 и
и 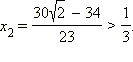 Значит, решением неравенства являются
Значит, решением неравенства являются 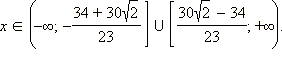
С учётом 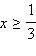 получается, что на данном множестве решениями являются
получается, что на данном множестве решениями являются 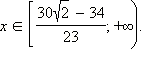 Объединяя результаты пунктов 1 и 2, получаем
Объединяя результаты пунктов 1 и 2, получаем
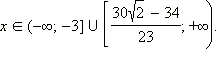
Запишем это решение другим способом:
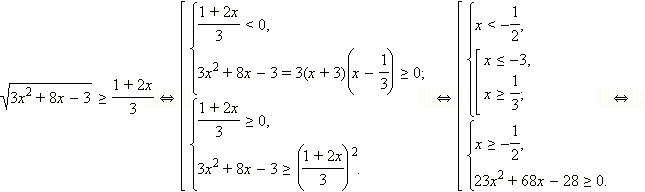
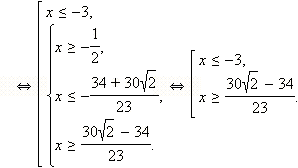
Ответ. 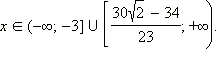
Неравенства вида 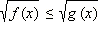
ОДЗ данного неравенства: 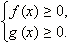 Обе части неравенства неотрицательны в ОДЗ, и потому можно возводить в квадрат. Получим равносильную систему
Обе части неравенства неотрицательны в ОДЗ, и потому можно возводить в квадрат. Получим равносильную систему

Заметим, что из неравенства 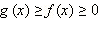 следует, что
следует, что 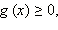 то есть дополнительно это требовать и включать это неравенство в систему не нужно.
то есть дополнительно это требовать и включать это неравенство в систему не нужно.
Отметим полезное следствие. Предположим, что ОДЗ неравенства уже найдено, и мы будем отбирать решения только из ОДЗ (это разумно, поскольку вне ОДЗ решений нет). Тогда исходное неравенство равносильно следующему: 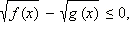 а та система, которой это неравенство равносильно, может быть представлена (для x из ОДЗ) в виде
а та система, которой это неравенство равносильно, может быть представлена (для x из ОДЗ) в виде 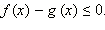 Следовательно, в ОДЗ
Следовательно, в ОДЗ
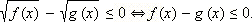
Ясно, что те же рассуждения применимы и для знака неравенства ≥. Отсюда можно сделать полезное заключение:
Знак разности 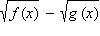 совпадает со знаком выражения
совпадает со знаком выражения 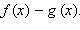
Отсюда же получается ещё одно полезное следствие:
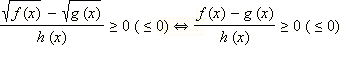 в ОДЗ:
в ОДЗ: 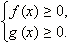
Пример 5
Решите неравенство 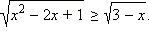
Перейдём к равносильной системе:
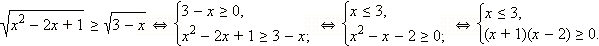
Решая эту систему методом интервалов, сразу получаем:
Ответ. 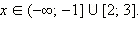
Пример 6
Решите неравенство 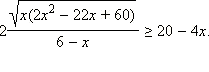
ОДЗ данного неравенства: 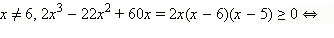
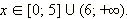
Заметим, что в ОДЗ x ≥ 0, поэтому существует 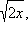 и значит,
и значит,
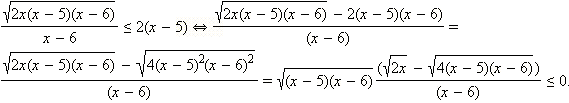
Мы воспользовались здесь тем, что в ОДЗ x ≥ 0, ( x – 5)( x – 6) ≥ 0 и потому существуют выписанные в последней строчке корни. Кроме того, мы вынесли за скобку 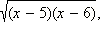 который по вышесказанному существует. Этот корень неотрицателен и потому не влияет на знак неравенства, следовательно, на него можно сократить, не забывая, что он может ещё обратиться в нуль и те x, для которых корень обращается в нуль, являются решениями неравенства. Таким образом, в ответ необходимо включить число x = 5. При x = 6 корень
который по вышесказанному существует. Этот корень неотрицателен и потому не влияет на знак неравенства, следовательно, на него можно сократить, не забывая, что он может ещё обратиться в нуль и те x, для которых корень обращается в нуль, являются решениями неравенства. Таким образом, в ответ необходимо включить число x = 5. При x = 6 корень 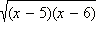 обращается в нуль, но x = 6 не входит в ОДЗ неравенства. Воспользуемся теперь тем, что знак разности корней совпадает со знаком разности подкоренных выражений. Имеем:
обращается в нуль, но x = 6 не входит в ОДЗ неравенства. Воспользуемся теперь тем, что знак разности корней совпадает со знаком разности подкоренных выражений. Имеем:
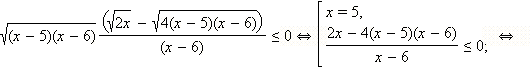
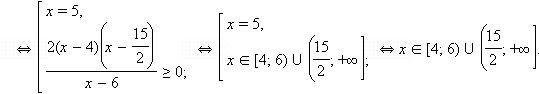 Учтём теперь ОДЗ и получим:
Учтём теперь ОДЗ и получим:
Ответ. 
Неравенства вида 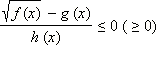
ОДЗ данного неравенства: 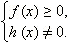 Предположим, что функции f ( x ) и g ( x ) не имеют общих корней. Рассмотрим вспомогательное неравенство
Предположим, что функции f ( x ) и g ( x ) не имеют общих корней. Рассмотрим вспомогательное неравенство
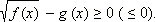 (*)
(*)
1. Если g ( x ) < 0, то для любого x из ОДЗ выполнено 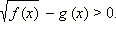
2. Если g ( x ) ≥ 0, то выражение 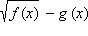 может иметь любой знак, но выражение
может иметь любой знак, но выражение 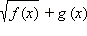 всегда строго положительно. Умножая обе части неравенства (*) на строго положительное число
всегда строго положительно. Умножая обе части неравенства (*) на строго положительное число 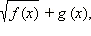 не меняя знака неравенства, перейдём к равносильному неравенству
не меняя знака неравенства, перейдём к равносильному неравенству
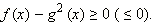 Таким образом, в ОДЗ
Таким образом, в ОДЗ
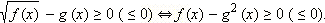
Значит, при g ( x ) ≥ 0, знак разности 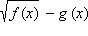 совпадает со знаком разности
совпадает со знаком разности 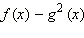 в ОДЗ.
в ОДЗ.
Получаем следующие условия равносильности.
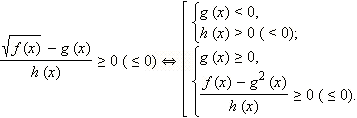
Запоминать приведённые системы неравенств не нужно, важно понимать, как они получаются.
Пример 7
Решите неравенство 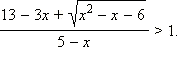
Выполним равносильные в ОДЗ преобразования и приведём неравенство к удобному для применения результатов настоящего пункта виду.
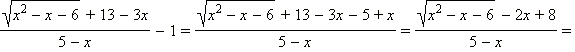
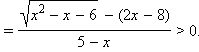
Мы не случайно сделали последнее преобразование. Важно понимать, чему здесь конкретно равняется функция g ( x ) = 2 x – 8. Типичной ошибкой является считать, что g ( x ) = 2 x + 8.
ОДЗ данного неравенства: 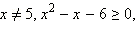 то есть
то есть 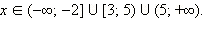 Теперь перейдём к равносильной системе. В ОДЗ
Теперь перейдём к равносильной системе. В ОДЗ
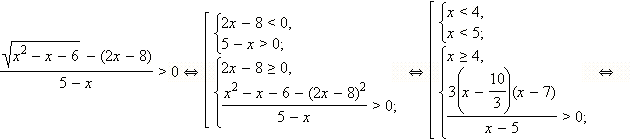
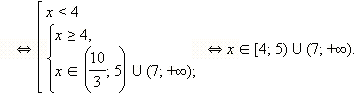 С учётом ОДЗ сразу получаем:
С учётом ОДЗ сразу получаем:
Ответ. 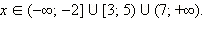
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|