
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тренировочный вариант №22 профильного ЕГЭ (2022 год)
Тренировочный вариант №22 профильного ЕГЭ (2022 год)
Часть 1
1. Найдите корень уравнения 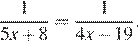
2. В сборнике билетов по географии всего 50 билетов, в 8 из них встречается вопрос по теме " Страны Европы". Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме " Страны Европы".
3. Угол между двумя соседними сторонами правильного многоугольника, равен 156°. Найдите число вершин многоугольника.
4. Найдите значение выражения 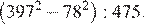
5. Середина ребра куба со стороной 1, 9 является центром шара радиуса 0, 95. Найдите площадь S части поверхности шара, лежащей внутри куба. В ответе запишите 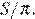
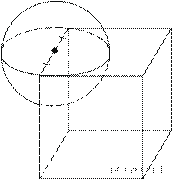
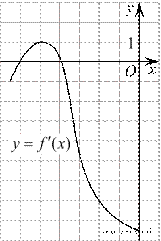
6. На рисунке изображён график 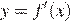 — производной функции
— производной функции 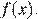 Найдите абсциссу точки, в которой касательная к графику
Найдите абсциссу точки, в которой касательная к графику 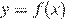 параллельна прямой y = 10 − 7x или совпадает с ней.
параллельна прямой y = 10 − 7x или совпадает с ней.
7. Расстояние от наблюдателя, находящегося на высоте h м над землeй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле 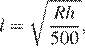 где
где 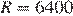 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 48 километров?
км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 48 километров?
8. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 1 минуту дольше, чем вторая труба?
9. На рисунке изображён график функции 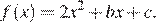 Найдите
Найдите 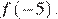
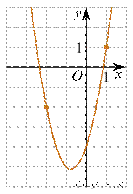
10. Вероятность того, что батарейка бракованная, равна 0, 06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
11. Найдите наименьшее значение функции 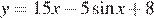 на отрезке
на отрезке 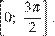
Часть 2
12. а) Решите уравнение 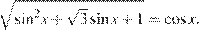
б) Укажите корни этого уравнения, принадлежащие отрезку 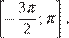
13. Все рёбра правильной треугольной пирамиды SBCD с вершиной S равны 9.
Основание O высоты SO этой пирамиды является серединой отрезка SS1, M — середина ребра SB, точка L лежит на ребре CD так, что CL: LD = 7: 2.
а) Докажите, что сечение пирамиды SBCD плоскостью S1LM — равнобедренная трапеция.
б) Вычислите длину средней линии этой трапеции.
14. Решите неравенство 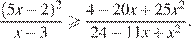
15. 15-го декабря планируется взять кредит в банке на 26 месяцев. Условия возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца с 1-го по 25-й долг должен быть на 20 тысяч рублей меньше долга на 15-е число предыдущего месяца;
— к 15-му числу 26-го месяца кредит должен быть полностью погашен.
Какой долг будет 15-го числа 25-го месяца, если общая сумма выплат после полного погашения кредита составит 1407 тысяч рублей?
16. Отрезки AK, BL, CN — высоты остроугольного треугольника АВС. Точки Р и Q — проекции точки N на стороны АС и ВС соответственно.
а) Докажите, что прямые PQ и KL параллельны.
б) Найдите площадь четырехугольника PQKL, если известно, что CN = 12, AC = 13, BC = 15.
17. Найти все значения a, при каждом из которых уравнение
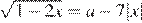
имеет более двух корней.
18. На полиграфической фабрике страницы тетради пронумерованы числами от 1 до 96. На случайной странице Максим, записал число 0 и пронумеровал все страницы далее до конца тетради числами 1, 2, 3,... и т. д., не пропуская ни одной. Затем он вернулся к странице с записанным 0 и пронумеровал страницы тетради назад числами − 1, − 2, − 3, ... и т. д. до начала тетради без пропусков. Сумма всех записанных чисел в тетради равна S. Определите номер страницы фабричной нумерации, на которой Максим записал число 0, если:
а) 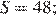 б)
б) 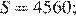 в)
в) 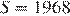
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|