
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема1: «Обзор общих понятий. Что включает в себя понятие функция?»
14. 02. 2022
Тема1: «Обзор общих понятий. Что включает в себя понятие функция? »
Тема2: «Область определения функции. Множество значений функции»
Задание №1. Пройдите по ссылке и посмотрите видеоурок по теме
https: //vk. com/video74831974_456239257
Задание №2. Запишите краткий конспект по теме (все, что выделено жирным шрифтом)
y = f(x)
y, f – функция
x- зависимая переменная, аргумент
f(x) – значение функции в точке x
1. Область определения функции D(y), D(f) – множество всех возможных значений переменной х.
2. Функциональная зависимость – правило, по которому каждому числу х из области определения D сопоставляется только одно число у.
3. Множество значений функции E(f), E(y)– множество значений, которые принимает переменная y.
4. Способы задания функции:
· Аналитический (формула)
· Табличный (таблица)
· Графический (график)
· Неявное задание функции (зависимость задана в форме уравнения, связывающего выражения с переменными)
5. Области определения некоторых функций:
A. Областью определения дроби являются все числа, при которых знаменатель отличен от нуля;
B. Областью определения корня четной степени являются все неотрицательные числа (т. е. подкоренное выражение должно быть ≥ 0);
C. Областью определения логарифмической функции являются только положительные значения аргумента (т. е. выражение, стоящее под знаком логарифма должно быть > 0)
Задание №3. Рассмотрите устно примеры решения некоторых задач (записывать не нужно)
Примеры.
1. Вычислите значение функции в указанной точке:
f(x)= 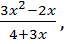 x= -1
x= -1
Решение. Подставим в заданную формулу вместо х данное число -1, получим:
f(-1)= 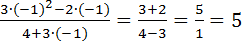
2. Найдите область определения функции:
a) f(x) = 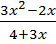 Данная функция является дробью (см. п. 5А), знаменатель не должен быть равен нулю. Выписываем знаменатель, приравниваем его к нулю, решаем уравнение, находим x. Затем знак равенства перечеркиваем.
Данная функция является дробью (см. п. 5А), знаменатель не должен быть равен нулю. Выписываем знаменатель, приравниваем его к нулю, решаем уравнение, находим x. Затем знак равенства перечеркиваем.
D(f): 4+3x ≠ 0, 3x ≠ -4, x ≠ -  .
.
Ответ записывают так 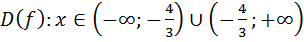
б) 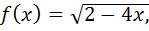 Это квадратный корень (см. п. 5В), подкоренное выражение должно быть больше либо равно нуля. Выписываем подкоренное выражение, записываем и решаем неравенство
Это квадратный корень (см. п. 5В), подкоренное выражение должно быть больше либо равно нуля. Выписываем подкоренное выражение, записываем и решаем неравенство
D(f): 2-4x≥ 0; -4x≥ -2; x≤ 0, 5; x 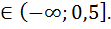
в) 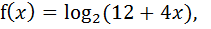 Это логарифмическая функция (см. п. 5С), выражение, стоящее внутри знака логарифм, должно быть больше нуля. Выписываем выражение, стоящее под знаком логарифма, записываем и решаем неравенство
Это логарифмическая функция (см. п. 5С), выражение, стоящее внутри знака логарифм, должно быть больше нуля. Выписываем выражение, стоящее под знаком логарифма, записываем и решаем неравенство
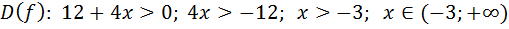
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|