Контакты

Случайная статья

Дифференциал функции. Свойства дифференциала

Дифференциал функции

Пусть функция 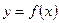дифференцируема на отрезке 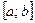. Тогда для всех 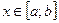определена производная: .

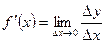Тогда 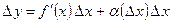. (1)

Первое слагаемое приращения функции 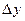(по формуле (1)) есть главная часть приращения функции 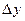, линейная относительно 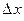. Это выражение 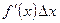называют также дифференциалом функции 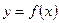и обозначают через 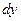или .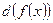

Таким образом, 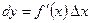. (2)

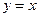Если , то 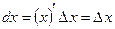, отсюда 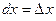. Следовательно, дифференциал независимой переменной 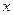совпадает с её приращением. Формулу (2) можно записать в виде

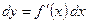. (3)

Свойства дифференциала

Теорема 1. Дифференциал суммы двух дифференцируемых функци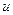й и 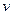равен сумме дифференциалов этих функций:

.

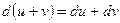Теорема 2. Дифференциал произведения двух дифференцируемых функци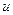й и 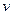определяется по формуле:

.

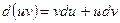Теорема 3. Дифференциал частного двух дифференцируемых функци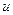й и 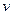определяется по формуле:

.

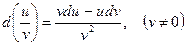© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.