
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
В2. Вычислить , если f(x)= .
Дневное отделение. 1 курс Группа ТЭО-20
Дата 11. 02. 2022
Математика.
Тема Дифференцирование сложной функции. Дифференциал функции.
Цель – знать, что такое дифференциал функции, что обозначает дифференцируемая функция, как находить производную сложной функции и дифференциал сложной функции. отработка алгоритма применения правила нахождения производной сложной функции и дифференциала функции при решении примеров и теста.
Добрый день, ребята.
Высылаю обещанное видео по определению производной. Ссылка ниже.
https: //vk. com/club208362343? z=video-208362343_456239017%2F213c08b488d7c26884%2Fpl_post_-208362343_21
После проработки лекции по ссылке еще ниже
https: //studfile. net/preview/10022442/
необходимо записать узловые моменты ( формулировки теорем и примеры) и перейти к выполнению практического задания ниже.
Тест по теме «Производная сложной функции».
Вариант №1.
Часть1.
При выполнении заданий этой части укажите № выбранного ответа.
А1. Найдите производную функции f(x)= 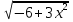 .
.
1) f/ (x)= 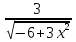 ; 2) f/ (x)=
; 2) f/ (x)= 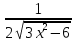 ; 3) f/ (x)=
; 3) f/ (x)= 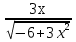 ; 4) f/ (x)=9х2-18.
; 4) f/ (x)=9х2-18.
А2. Найдите область определения функции f(x)=  .
.
1) (- 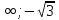 )
) 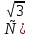 :
: 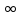 ); 2)
); 2) 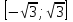 ; 3) (
; 3) ( 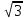 ;
; 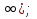 4) (-
4) (- 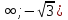
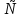 [
[ 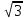 ;
; 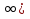 .
.
Часть 2.
Ответом на каждое задание этой части будет некоторое целое число. Это число следует записать в бланк ответов. Если ответом будет дробь, то её следует округлить до целых.
В1. Вычислить f/(0), если f(x)= (8х4-5х+1)2.
В2. Вычислить, если f(x)=.
Часть 3.
Запишите развёрнутое решение и ответ.
На «4»- выполнение заданий А1-А2, на «5»- необходимо выполнить все задания
Выполнить 17. 02. 2022; до 18. 00. Успехов!
С уважением к вам и вашему труду Татьяна Петровна.
Удачи.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|