Хелпикс

Главная

Контакты

Случайная статья



Р(А+В)=Р(А)+Р(В)



 

Тема урока: «Элементы комбинаторики» (2 часа).

 

Произведение всех натуральных чисел от 1 до n включительно называется факториалом числа n и записывается n! (читается как «эн факториал»).

n! =1⋅ 2⋅ 3⋅... ⋅ (n− 2)⋅ (n− 1)⋅ n.

 

Принято, что 0! =1.

1! =1;

2! =2⋅ 1=2;

3! =3⋅ 2⋅ 1=6;

4! =4⋅ 3⋅ 2⋅ 1=24;

5! =5⋅ 4⋅ 3⋅ 2⋅ 1=120;

6! =6⋅ 5⋅ 4⋅ 3⋅ 2⋅ 1=720.

 

Пример:

 Вычисли значение выражения.

а) 5! +4! =5⋅ 4⋅ 3⋅ 2⋅ 1+4⋅ 3⋅ 2⋅ 1=120+24=144.

 

б) 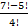=  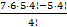=  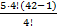= 5⋅ 41 = 205 (4! выносится за скобки. В дроби равные факториалы можно сокращать).

 

в) 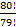 +  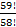=  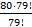+  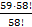= 80+59 = 139.

 

Каждый больший факториал можно выразить меньшим факториалом, т. е.
n! = n(n− 1)! = n(n− 1)(n− 2)! = n(n− 1)(n− 2)(n− 3)! и т. д.

Комбинаторика — раздел математики о вычислении количества различных комбинаций каких-либо элементов.

Основные элементы комбинаторики:

1) Размещение:

а) с повторениями б) без повторений

2) Перестановка

3) Сочетание

 

Всякий упорядоченный набор, имеющий k элементов, взятых из наперед заданных n элементов, будем называть размещением с повторениями из n по k.

Размещение с повторениями: m = nk

Например:

Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8?
Решение. Всего цифр 5, то есть n = 5, из них надо составить четырехзначные числа, то есть k = 4. Для каждого разряда четырехзначного числа имеется пять возможностей, значит m = 5*5*5*5 = nk = 54 = 625.

Цифры в числе могут повторяться, например, 1122, 1223, 4444 …

Ответ: 625

 

Всякий упорядоченный набор, имеющий k элементов, взятых из наперед заданных n элементов без повторений, будем называть размещением из n по k (без повторений).
Размещение без повторений: Аkn = .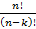

Например:

Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?
Решение: т. к. нечетных цифр пять, а именно 1, 3, 5, 7, 9 (n = 5), то эта задача сводится к выбору и размещению на две разные позиции (k= 2) двух из пяти различных цифр, т. е. указанных чисел будет: А25 = 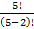 =  =  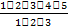= 4 ꞏ 5 = 20.

Цифры в числе не могут повторяться, то есть 13, 51, 73… Но нельзя 33, 11, 77…

Ответ:  20

 

Всякий упорядоченный набор имеющий n элементов, взятых из наперед заданных n элементов без повторений, будем называть перестановкой из n.
Перестановка из n элементов: Рn = n!

Например:

Сколькими различными способами можно составить список учеников (не по алфавиту, любым способом), если в нём должно быть 25 различных учеников?

Решение: Р25 = 25! = 1⋅ 2⋅ 3⋅... ⋅ 24⋅ 25=25!

Ответ: список можно составить 25! различными способами.

 

Всякий неупорядоченный набор имеющий k элементов, взятых из наперед заданных n элементов без повторений, будем называть сочетанием из n по k.
Сочетание из n элементов по k: Ckn =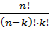

Например:

Сколькими способами читатель может выбрать две книжки из шести имеющихся?
Решение: Число способов равно числу сочетаний из шести книжек по две, т. е. равно:

C26 = 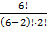 =  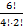=  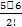=  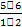= 15

Заметьте, книги, естественно, не повторяются и какую из двух мы взяли первой или второй роли не играет.

Ответ: 15.

 

 Различные способы решения задач:

В заданиях по комбинаторике обычно нужно выяснить, возможно ли составить комбинацию определённого вида, и сколько различных комбинаций можно составить.

 

Один из способов решения задач комбинаторики — это рассмотреть все возможные комбинации элементов, что называется полным перебором вариантов.

 

Древовидная диаграмма

Древовидная диаграмма — один из способов показать и систематизировать все размещения. С помощью древовидной диаграммы осуществляется полный перебор.

 

Пример 1: Сколько различных двузначных чисел можно составить из цифр 1, 2 и 3, если каждую использовать только один раз?

Решение:

составляется древовидная диаграмма.

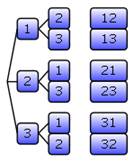
Ответ: можно составить 6 различных чисел.

 

Пример 2: Сколькими различными способами можно образовать пару дежурных, если в

классе остались Надя, Вика, Саша и Юра?

 

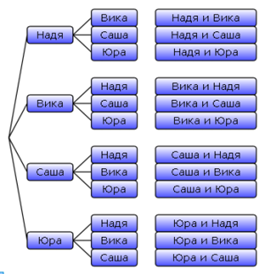
На древовидной диаграмме видно, что можно образовать только 6 пар дежурных (Надя и Вика, Надя и Саша, Надя и Юра, Вика и Саша, Саша и Юра, Вика и Юра), т. к. каждая пара повторяется 2 раза.

Эту задачу можно решить с помощью сочетания: C24 = 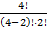 =  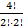=  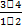= 6

Ответ: 6

 

Пример 3:

Сколькими различными способами можно выбрать двух учеников (одного — чистить доску, второго — подметать пол), если в классе остались Надя, Вика, Саша и Юра?

 

Используется та же древовидная диаграмма, но в данном случае ответ будет — 12 пар, т. к. каждая пара из диаграммы отличается. Если детей поменять местами, они выполняют уже другие функции.

Эту задачу можно решить с помощью размещения без повторения: А24 = 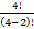 =  =  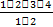= 3· 4 = 12.

С помощью древовидной диаграммы были получены различные результаты, т. к. в 3 и 4 примере были рассмотрены различные виды комбинаций: сочетания и размещения.

 

Такого рода диаграммы в подробностях удобно рисовать только для сравнительно небольшого числа вариантов, а, например, для сотен комбинаций дерево вариантов целиком не нарисуешь. Тогда приходится действовать по-другому. Чаще всего при различных подсчётах используют правило умножения.

 

Правило умножения: для того чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.

Например:

Сколькими различными способами можно составить танцевальную пару, если в коллективе 3 мальчика и 4 девочки?

Решение: 3 · 4 = 12

Ответ: 12

Таблица

В отдельных случаях для систематизации данных составляются таблицы комбинаций.

Простой игровой кубик бросается 2 раза, и полученные пункты перемножаются (или суммируются, в зависимости от задачи). Сколько различных произведений можно получить?

 

 

 

 

Различные произведения — это 1; 2; 3; 4; 5; 6; 8; 9; 10; 12; 15; 16; 18; 20; 24; 25; 30; 36 — всего 18 различных результатов.

 

 

Тема урока: «Классическое определение вероятности» (2 часа).

 

Испытанием называется осуществление определенных действий.

Событие - факт, который может произойти в результате испытания.

Любой результат испытания называется исходом .

Достоверным называют событие, которое в результате испытания обязательно произойдёт.

Невозможным называют событие, которое заведомо не произойдёт в результате испытания.

Пространство элементарных событий — множество всех различных исходов произвольного испытания.

Если события не могут произойти одновременно в одном испытании, то события называются несовместными .

Противоположное событие происходит тогда, когда исходное событие А не происходит.

Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой сверху.

Например:

A – сдал экзамен по математике;

Ᾱ – не сдал экзамен по математике.

 

Суммой событий А и В называется событие А+В, которое состоит в том, что наступит или событие А, или событие В, или оба события одновременно.

Произведением событий А и В называется событие А•В, состоящее в совместном осуществлении событий А и В.

Например:

Пусть А - идет дождь, B - идет снег, тогда А + В – «идет снег или дождь»

 

При 3-х выстрелах по мишени события: А0 – «попаданий нет», А1 – «одно попадание», А2 – «два попадания», тогда А=А0+А1+А2 - «произошло не больше двух попаданий»

 

Пусть С - из урны вынули белый шар, D - из урны вынули белый шар, тогда C⋅ D - из урны вынули два белых шара

Пусть С - из урны вынули белый шар, D - из урны вынули белый шар, тогда C⋅ 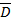- из урны вынули два шара: белый и не белый.

Теорема сложения вероятностей несовместных событий: вероятность появления одного из двух несовместных событий А или В равна сумме вероятностей этих событий:

Р(А+В)=Р(А)+Р(В)

 

Классическое определение вероятности применяется для равновозможных событий.

К равновозможным (равновероятностным) относятся такие события, для которых нет никаких объективных оснований считать, что одно является более возможным, чем другие.

Например, при бросании игрального кубика события выпадения любого из очков равно возможны.

 

Рассмотрим произвольный эксперимент.

Пусть n − число всех исходов эксперимента, которые образуют полную группу попарно несовместных и равновозможных событий, m – число благоприятных событию А исходов.

Тогда вероятностью события А называется число:

P(A) =

Из классического определения вероятности вытекают следующие ее свойства:

 1. Вероятность достоверного события А всегда равна единице, то есть P(А) = 1;

 это объясняется тем, что достоверному событию благоприятствуют все элементарные события, то есть m = n;

 

2. Вероятность невозможного события В всегда равна нулю, то есть P(В) = 0;

это объясняется тем, что невозможному событию не благоприятствует ни одно из элементарных, то есть m = 0;

 

3. Вероятность любого случайного события A всегда удовлетворяет условию 0 ≤ P(A) ≤ 1.
Если в процентах, то 0 ≤ P(A) ≤ 100

 

Задача:   Из колоды в 36 карт вынимается одна карта. Какова вероятность появления карты червовой масти?

 

Решение. Количество элементарных исходов (количество карт) n=36. Событие A — появление карты червовой масти. Число случаев, благоприятствующих появлению события A, m=9. Следовательно, P(A)= 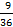= =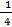0, 25.

Если в процентах, то 0, 25 · 100 = 25%.

Теорема

Для нахождения вероятности противоположного события следует из единицы вычесть вероятность самого события: P(A) = 1 − P( ).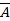

 

Задача: В коробке находятся 4 мячика белого цвета и 13 мячиков красного цвета.

Вытаскивают три мячика. Какова вероятность, что хотя бы один будет белого цвета?

 

Решение: Благоприятные исходы, когда из трех мячей один белого цвета, два или три (так как в задаче сказано: хотя бы один).

Нас не устраивает только исход, в котором вытащим три красных мяча. Это и есть противоположное событие. Найдем его вероятность и вычтем из 1.

m = C313 = 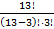 =  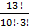= = 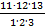286

n = C317 = 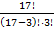 =  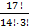= = 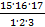680

Р( ) =  =  =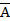

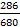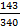
P(A) = 1 − 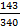 = 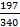≈ 0, 579 (57, 9%)

Ответ: 0, 579

Есть второй способ решения: Р( ) =  ·  ·  = …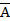

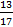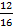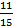Затем, P(A) = 1 − Р( ) =…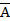

 

Решите вероятностную задачу с помощью таблицы.

Подбрасываются две игральные кости. Какова вероятность события А, заключающегося в том, что сумма выпавших очков нечетная?

Решение:

 

 

Всего исходов (сумм) 36, n = 36.  Нечетных сумм (выделенные зеленым) 18, m = 18.

P(A) =  =  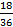=  = 0, 5 (50%)

Ответ: 0, 5

 

Задача: Найти вероятность того, что наудачу взятое двузначное число от 10 до 99 окажется кратным либо 3, либо 8, либо тому и другому одновременно.

Решение: Всего чисел 90 (можете посчитать и проверить).

Событие А: из них делятся на 3 – 30.

Событие В: из них делятся на 8 – 11.

В этих двух событиях есть повторяющиеся числа, а берут только один раз, поэтому повторение надо исключить. Таких чисел (те, которые делятся и на 3, и на 8, то есть на 24, событие С) – 4.

P(A) = 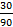P(В) = 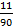P(С) =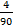

Р = P(A) + P(В) − P(С) = 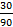 +  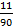−  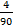= 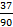≈ 0, 41 (41%).

Ответ: 0, 41

 



  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.