
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Краевая задача о кручении прямолинейного стержня
ТЕМА №2
Краевая задача о кручении прямолинейного стержня
произвольного сечения
Задание. Стальной стержень прямоугольного поперечного сечения с размерами 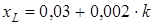 м;
м; 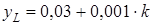 м и длиной
м и длиной 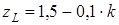 м подвержен действию крутящего момента
м подвержен действию крутящего момента 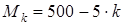 н× м. Требуется определить значения относительного и действительного углов кручения, а также наибольшее касательное напряжение в сечении стержня и значение момента инерции, если известен модуль упругости сдвига
н× м. Требуется определить значения относительного и действительного углов кручения, а также наибольшее касательное напряжение в сечении стержня и значение момента инерции, если известен модуль упругости сдвига 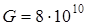 н/м2. В задании
н/м2. В задании 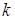 – номер варианта. Для решения задачи использовать программу, приведенную на рис. 7. 17. Построить график поверхности напряжения Эри
– номер варианта. Для решения задачи использовать программу, приведенную на рис. 7. 17. Построить график поверхности напряжения Эри  в зависимости от координат
в зависимости от координат 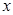 и
и 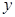 , касательного напряжения
, касательного напряжения 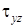 в сечении
в сечении 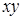 . Провести анализ полученных решений.
. Провести анализ полученных решений.
В инженерной практике широко распространены конструкции, испытывающие кручение: это оси машин и механизмов, пружины, испытывающие кручение совместно с изгибом, несущие конструкции пролетных строений мостов и т. п. Стержень испытывает кручение, если на него действуют пары сил, расположенных в плоскостях, перпендикулярных его продольной оси. Способы расчета деталей машин на прочность и жесткость зависят от их формы и вида нагружения. Чем сложнее форма детали, тем сложнее, как правило, и методы ее расчета. Поэтому при составлении расчетной схемы инженер стремится к тому, чтобы упростить реальные формы деталей и свести их к простейшим, не внося при этом в расчеты существенных погрешностей. Простейшую форму имеет брус (прямолинейный стержень) – тело, одно из измерений которого (длина) значительно превышает другие (размеры поперечного сечения).
Рассматривается однородный стержень постоянного поперечного сечения произвольной формы, скручиваемый крутящим моментом 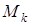 . При кручении деформация характеризуется поворотом вокруг оси одного сечения по отношению к другому на некоторый угол закручивания
. При кручении деформация характеризуется поворотом вокруг оси одного сечения по отношению к другому на некоторый угол закручивания 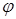 . При этом сечения круглых и кольцевых профилей поворачиваются, оставаясь плоскими, некруглых – искривляются из своей плоскости по некоторой поверхности ( депланируют ).
. При этом сечения круглых и кольцевых профилей поворачиваются, оставаясь плоскими, некруглых – искривляются из своей плоскости по некоторой поверхности ( депланируют ).
В связи с развитием депланаций различают два типа кручения стержней: свободное и стесненное. Если депланации всех поперечных сечений по длине стержня одинаковы или отсутствуют, то кручение называется свободным. При переменных по длине депланациях кручение называют стесненным. При свободном кручении в поперечных сечениях возникают только касательные напряжения 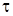 . При стесненном кручении наряду с касательными напряжениями
. При стесненном кручении наряду с касательными напряжениями 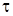 появляются и нормальные напряжения
появляются и нормальные напряжения 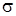 , распределенные неравномерно по площади сечения и длине стержня.
, распределенные неравномерно по площади сечения и длине стержня.
Постановка задачи. Необходимо определить значения относительного и действительного углов кручения, а также наибольшее касательное напряжение при расчете испытывающих кручение прямолинейных стержней на прочность и жесткость.
В теории упругости используется определение свободного кручения, предложенное Сен-Венаном, в соответствии с которым кручение стержней состоит из двух частей – поворотов поперечных сечений без перекосов углов в них и депланаций поперечных сечений, которые для всех сечений одинаковы. Если под действием крутящего момента форма сечений по длине стержня не меняется, а распределение сил на торцах не оказывает влияние на части тела, находящиеся вдали от них, то кручение можно считать свободным.
Условия прочности и жесткости при кручении можно записать в виде
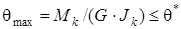 и
и 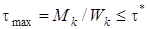 , (I)
, (I)
где 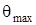 и
и 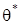 – наибольший и допускаемый относительные (погонные) углы закручивания;
– наибольший и допускаемый относительные (погонные) углы закручивания;  и
и 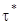 – наибольшее и допускаемое касательные напряжения в поперечном сечении стержня;
– наибольшее и допускаемое касательные напряжения в поперечном сечении стержня; 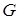 – модуль упругости при кручении;
– модуль упругости при кручении; 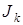 – момент инерции при кручении;
– момент инерции при кручении; 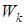 – момент сопротивления кручению. Для некоторых сечений, например, круглого, кольцевого, прямоугольного и т. п., при расчете стержней на прочность и жесткость можно использовать приближенные формулы, полученные методами теории упругости [51]. Например, для стержней прямоугольного поперечного сечения момент инерции при кручении приближенно можно вычислять по формуле:
– момент сопротивления кручению. Для некоторых сечений, например, круглого, кольцевого, прямоугольного и т. п., при расчете стержней на прочность и жесткость можно использовать приближенные формулы, полученные методами теории упругости [51]. Например, для стержней прямоугольного поперечного сечения момент инерции при кручении приближенно можно вычислять по формуле:
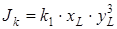 ,
,
а момент сопротивления кручению по формуле:
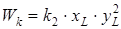 ,
,
где 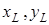 – размеры прямоугольного поперечного сечения бруса, причем
– размеры прямоугольного поперечного сечения бруса, причем 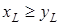 ;
; 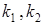 – коэффициенты, зависящие от отношения длинной стороны к короткой, определяются по известным таблицам из теории упругости [51]. Таблица 1
– коэффициенты, зависящие от отношения длинной стороны к короткой, определяются по известным таблицам из теории упругости [51]. Таблица 1
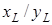
| 1. 0 | 1. 25 | 1. 5 | 1. 75 | 2. 0 | 2. 5 | 3. 0 | 
|
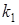
| 0. 141 | 0. 172 | 0. 196 | 0. 214 | 0. 229 | 0. 249 | 0. 263 | 1/3 |
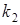
| 0. 208 | 0. 221 | 0. 231 | 0. 239 | 0. 246 | 0. 258 | 0. 267 | 1/3 |
Пусть к торцам прямолинейного стержня приложены силы, статически эквивалентные крутящему моменту 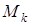 , а боковая его поверхность свободна от внешних усилий. При кручении стержня постоянного сечения парами, приложенными по его концам (чистое кручение) в поперечных сечениях возникают только касательные напряжения, одинаковые во всех сечениях. При чистом кручении поперечное сечение поворачивается относительно продольной оси на малый угол
, а боковая его поверхность свободна от внешних усилий. При кручении стержня постоянного сечения парами, приложенными по его концам (чистое кручение) в поперечных сечениях возникают только касательные напряжения, одинаковые во всех сечениях. При чистом кручении поперечное сечение поворачивается относительно продольной оси на малый угол 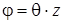 , где
, где 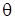 – погонный угол закручивания,
– погонный угол закручивания, 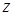 – расстояние рассматриваемого сечения от начала координат. Ось
– расстояние рассматриваемого сечения от начала координат. Ось 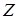 будем располагать вдоль оси стержня (рис. 7. 15).
будем располагать вдоль оси стержня (рис. 7. 15).
В стержнях некруглых сечений при кручении поперечные сечения коробятся ( депланируют), т. е. точки сечения выходят из плоскости сечения. Если депланации сечения ничто не мешает, то в сечении на расстоянии 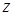 от начала координат нормальные напряжения
от начала координат нормальные напряжения 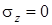 и имеем свободное кручение, при котором в сечении возникают только
и имеем свободное кручение, при котором в сечении возникают только 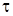 – касательные напряжения. Ввиду отсутствия нормальных напряжений при свободном кручении, уравнения равновесия имеют вид:
– касательные напряжения. Ввиду отсутствия нормальных напряжений при свободном кручении, уравнения равновесия имеют вид:
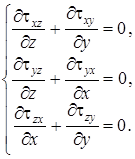 (7. 50)
(7. 50)
где 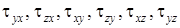 – компоненты касательных напряжений, действующих на шести гранях малого прямоугольного параллелепипеда, используемого для составления дифференциальных уравнений равновесия деформированного тела [51]. С помощью исследования равновесия элемента (малого прямоугольного параллелепипеда) число символов для касательных напряжений сокращается до трех:
– компоненты касательных напряжений, действующих на шести гранях малого прямоугольного параллелепипеда, используемого для составления дифференциальных уравнений равновесия деформированного тела [51]. С помощью исследования равновесия элемента (малого прямоугольного параллелепипеда) число символов для касательных напряжений сокращается до трех: 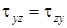 ,
,  ,
, 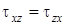 .
.
| 
|
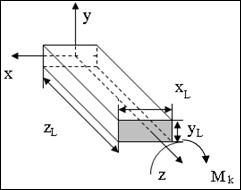
Рис. 7. 15. Касательные напряжения при кручении стержня прямоугольного сечения
Для определения перемещений вдоль координатных осей можно воспользоваться решением задачи Сен-Венана о кручении стержня:
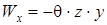 ,
, 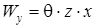 ,
, 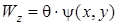 ,
,
где 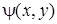 – функция, определяющая депланацию поперечного сечения,
– функция, определяющая депланацию поперечного сечения, 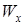 ,
, 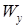 ,
, 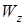 – перемещения в направлении осей, соответственно,
– перемещения в направлении осей, соответственно, 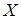 ,
, 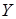 ,
, 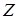 ;
; 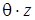 – угол закручивания поперечного сечения на расстоянии
– угол закручивания поперечного сечения на расстоянии 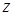 от начала координат.
от начала координат.
В случае если депланации чем-то ограничены, например, при заделке торца стержня, то рядом расположенные сечения коробятся по-разному, возникает стесненное кручение. В зоне стесненного кручения в поперечном сечении наряду с касательными напряжениями 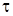 возникают нормальные напряжения,
возникают нормальные напряжения, 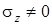 . При этом нормальные напряжения стесненного кручения быстро убывают по мере удаления от заделки.
. При этом нормальные напряжения стесненного кручения быстро убывают по мере удаления от заделки.
Возникновение перемещений 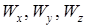 связано с образованием сдвигов в плоскостях
связано с образованием сдвигов в плоскостях 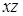 и
и 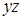 :
:
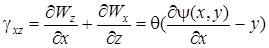 ,
,
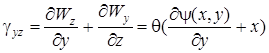 .
.
Сдвиг в плоскости поперечного сечения 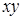 отсутствует, т. е.
отсутствует, т. е.
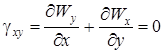 ,
,
где 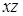 ,
, 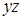 ,
, 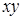 – сечения, параллельные координатным плоскостям;
– сечения, параллельные координатным плоскостям; 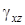 ,
, 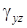 ,
, 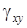 – углы сдвигов.
– углы сдвигов.
Составляющие касательного напряжения определяются на основании закона Гука:
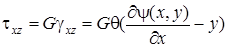 ,
,
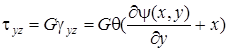 , (7. 51)
, (7. 51)
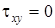 ,
,
где 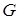 – модуль сдвига материала стержня.
– модуль сдвига материала стержня.
Относительный угол закручивания 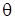 (взаимный поворот двух сечений) можно вычислять по формуле
(взаимный поворот двух сечений) можно вычислять по формуле
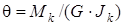 , (7. 52)
, (7. 52)
где 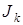 – неизвестный пока момент инерции при кручении. Уравнения равновесия (7. 50) для прямолинейного стержня при свободном кручении имеют вид:
– неизвестный пока момент инерции при кручении. Уравнения равновесия (7. 50) для прямолинейного стержня при свободном кручении имеют вид: 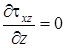 ,
,  ,
, 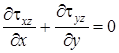 . При этом нормальные напряжения ввиду чистого сдвига равны нулю. Первые два из этих уравнений уже удовлетворяются, так как
. При этом нормальные напряжения ввиду чистого сдвига равны нулю. Первые два из этих уравнений уже удовлетворяются, так как 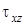 и
и 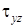 , определяемые уравнениями (7. 51), не зависят от координаты
, определяемые уравнениями (7. 51), не зависят от координаты 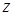 . Из третьего уравнения следует, что
. Из третьего уравнения следует, что 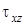 и
и 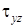 можно выразить в виде:
можно выразить в виде:
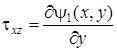 и
и 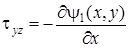 , (7. 53)
, (7. 53)
где функция  называется функцией напряжений Эри. Непосредственным дифференцированием соотношений (7. 53) с учетом (7. 51) можно показать, что функция напряжений
называется функцией напряжений Эри. Непосредственным дифференцированием соотношений (7. 53) с учетом (7. 51) можно показать, что функция напряжений  удовлетворяет уравнению:
удовлетворяет уравнению:
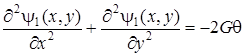 . (7. 54)
. (7. 54)
Если ввести функцию 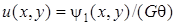 , то уравнение (7. 54) примет вид:
, то уравнение (7. 54) примет вид: 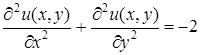 . (7. 55)
. (7. 55)
Когда боковая поверхность стержня свободна от внешней нагрузки, уравнение (7. 55) необходимо интегрировать при граничном условии:
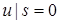 . (7. 56)
. (7. 56)
На контуре сечения функция напряжения  должна иметь постоянное значение, так как согласно выражению (7. 53) напряжения зависят только от производных функции
должна иметь постоянное значение, так как согласно выражению (7. 53) напряжения зависят только от производных функции  , ее изменение на постоянную величину не изменяет напряжений, поэтому можно принять условие (7. 56).
, ее изменение на постоянную величину не изменяет напряжений, поэтому можно принять условие (7. 56).
Таким образом, исследование напряженного и деформированного состояния прямолинейного стержня с произвольной формой поперечного сечения при кручении сводится к изучению математической модели в виде краевой задачи (7. 55)–(7. 56). Решение этой краевой задачи дает возможность определить момент инерции при кручении по соотношению:
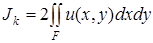 , (7. 57)
, (7. 57)
где 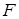 – область поперечного сечения стержня. Относительный угол закручивания
– область поперечного сечения стержня. Относительный угол закручивания 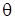 определяется из выражения (7. 52) с учетом формулы (7. 57) для определения момента инерции.
определяется из выражения (7. 52) с учетом формулы (7. 57) для определения момента инерции.
Касательные напряжения 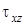 и
и 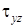 , возникающие при кручении, определяются из выражений (7. 53). Действительный угол кручения
, возникающие при кручении, определяются из выражений (7. 53). Действительный угол кручения 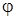 в общем случае определяется из решения дифференциального уравнения
в общем случае определяется из решения дифференциального уравнения
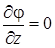 (7. 58)
(7. 58)
При соответствующих граничных условиях, в частности, когда скручиваемый стержень имеет постоянное поперечное сечение, а начало координат выбрано на конце стержня, это решение записывается в виде:
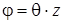 , (7. 59)
, (7. 59)
где координата 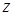 – расстояние от начального до рассматриваемого сечения по оси стержня.
– расстояние от начального до рассматриваемого сечения по оси стержня.
Таким образом, расчет кручения стержня сводится в основном к решению краевой задачи (7. 55)–(7. 56), которая представляет собой задачу Дирихле для уравнения Пуассона.
Для численного решения краевой задачи (7. 55)–(7. 56) о кручении стержня используем метод конечных разностей. Пусть сечение стержня для конкретности имеет форму прямоугольника размерами 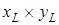 . При этом область поперечного сечения
. При этом область поперечного сечения 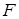 заменяется сеточной областью. Выбрав шаги
заменяется сеточной областью. Выбрав шаги 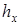 ,
, 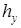 по
по 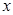 и
и 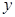 соответственно, строим сетку
соответственно, строим сетку 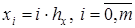 ;
; 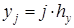 ,
, 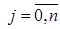 , где
, где 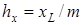 и
и 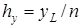 ,
, 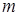 и
и 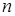 – соответственно, число разбиений сторон прямоугольника
– соответственно, число разбиений сторон прямоугольника 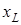 и
и 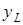 .
.
Введем обозначения 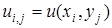 и аппроксимируем частные производные
и аппроксимируем частные производные 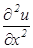 и
и 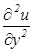 в каждом внутреннем узле сетки центральными разностными производными второго порядка
в каждом внутреннем узле сетки центральными разностными производными второго порядка
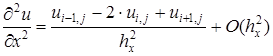 ,
,
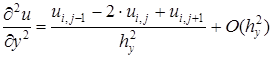 .
.
Уравнение Пуассона (7. 55) аппроксимируем на пятиточечном шаблоне под названием «крест», представленном на рис. 7. 16
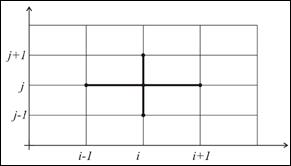
Рис. 7. 16
В результате получим следующую разностную схему:
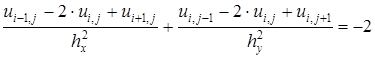 , (7. 60)
, (7. 60)
где индексы меняются в пределах 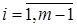 ,
, 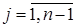 .
.
Погрешность замены дифференциального уравнения разностным уравнением составляет величину 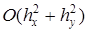 , т. е. второй порядок точности по координате
, т. е. второй порядок точности по координате 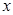 и второй порядок точности по координате
и второй порядок точности по координате 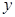 .
.
Уравнения (7. 60) вместе со значениями 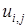 в граничных узлах образуют систему линейных алгебраических уравнений относительно приближенных значений функции
в граничных узлах образуют систему линейных алгебраических уравнений относительно приближенных значений функции 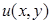 в узлах сетки
в узлах сетки 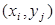 . Разностную схему (7. 60) с учетом граничных условий (7. 56) представим в виде
. Разностную схему (7. 60) с учетом граничных условий (7. 56) представим в виде
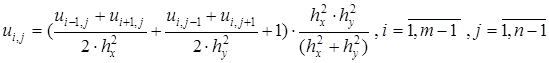 ,
,
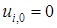 ,
,  ,
, 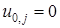 ,
, 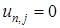 ,
, 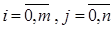 . (7. 61)
. (7. 61)
Численное решение задачи Дирихле для уравнения Пуассона в прямоугольнике состоит в нахождении приближенных значений 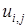 искомой функции
искомой функции 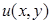 во внутренних узлах сетки. Для определения величин
во внутренних узлах сетки. Для определения величин 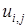 требуется решить систему линейных алгебраических уравнений (7. 61). Для ее решения существуют прямые и итерационные методы, такие как метод Гаусса, матричной прогонки, Зейделя и т. д. Ввиду большой размерности системы (7. 61) для ее решения лучше использовать итерационный метод Зейделя, который состоит в построении последовательности итераций вида
требуется решить систему линейных алгебраических уравнений (7. 61). Для ее решения существуют прямые и итерационные методы, такие как метод Гаусса, матричной прогонки, Зейделя и т. д. Ввиду большой размерности системы (7. 61) для ее решения лучше использовать итерационный метод Зейделя, который состоит в построении последовательности итераций вида
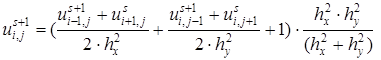 ,
,
где верхним индексом 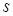 обозначен номер итерации. При значениях
обозначен номер итерации. При значениях 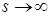 последовательность
последовательность 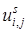 сходится к точному решению системы (7. 61). В качестве условия окончания итерационного процесса можно принять
сходится к точному решению системы (7. 61). В качестве условия окончания итерационного процесса можно принять
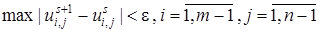 ,
, 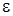 – погрешность (отклонение приближенного решения от точного).
– погрешность (отклонение приближенного решения от точного).
Таким образом, погрешность приближенного решения, полученного методом сеток, складывается из двух погрешностей: погрешности аппроксимации дифференциального уравнения разностными уравнениями и погрешности, возникающей в результате приближенного решения системы уравнений (7. 61).
Рассмотренная здесь разностная схема обладает свойством устойчивости и сходимости. Устойчивость схемы означает, что малые изменения в начальных данных приводят к малым изменениям решения разностной задачи. Сходимость схемы означает, что при стремлении одновременно шага 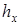 и шага
и шага 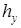 к нулю, решение разностной задачи стремится в некотором смысле к решению исходной задачи. Таким образом, выбрав достаточно малый шаг
к нулю, решение разностной задачи стремится в некотором смысле к решению исходной задачи. Таким образом, выбрав достаточно малый шаг 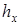 и малый шаг
и малый шаг 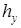 , можно как угодно точно решить исходную задачу.
, можно как угодно точно решить исходную задачу.
Алгоритм численного решения задачи Дирихле для уравнения Пуассона методом сеток реализуется в виде программы на языке VBA в Excel (рис. 7. 17). Входными параметрами в программу являются: 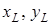 (м) – размеры поперечного сечения прямоугольной формы (
(м) – размеры поперечного сечения прямоугольной формы ( 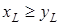 );
); 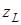 (м) – длина стержня;
(м) – длина стержня; 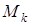 (н× м) – крутящий момент;
(н× м) – крутящий момент; 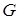 (н/м2) – модуль сдвига материала;
(н/м2) – модуль сдвига материала; 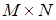 – размеры сеточной области для поперечного сечения (число разбиений по
– размеры сеточной области для поперечного сечения (число разбиений по 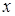 и по
и по 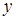 );
); 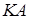 – максимальное число итераций в методе Зейделя;
– максимальное число итераций в методе Зейделя;  – коэффициент, зависящий от отношения длинной стороны прямоугольного сечения к короткой, используется при определении наибольшего касательного напряжения в сечении прямоугольной формы по формуле (I), некоторые его значения приведены табл. 1.
– коэффициент, зависящий от отношения длинной стороны прямоугольного сечения к короткой, используется при определении наибольшего касательного напряжения в сечении прямоугольной формы по формуле (I), некоторые его значения приведены табл. 1.

Рис. 7. 17
Выходные параметры следующие: двумерный массив из 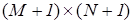 действительных чисел, содержащий значения функции напряжений Эри
действительных чисел, содержащий значения функции напряжений Эри 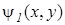 в узлах сетки;
в узлах сетки; 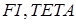 – значения действительного и относительного углов кручения
– значения действительного и относительного углов кручения 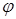 и
и 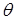 ;
; 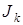 – момент инерции при кручении;
– момент инерции при кручении; 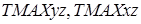 – наибольшие касательные напряжения в сечениях, параллельных координатным плоскостям;
– наибольшие касательные напряжения в сечениях, параллельных координатным плоскостям; 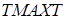 – максимальное касательное напряжение в сечении стержня, определяемое по формуле (I), которое используется для сравнения с расчетными значениями максимального касательного напряжения, полученными с помощью программного модуля, приведенного на рис. 7. 17.
– максимальное касательное напряжение в сечении стержня, определяемое по формуле (I), которое используется для сравнения с расчетными значениями максимального касательного напряжения, полученными с помощью программного модуля, приведенного на рис. 7. 17.
Пример. Стальной стержень прямоугольного поперечного сечения с размерами  м;
м; 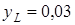 м и длиной
м и длиной 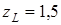 м подвержен действию крутящего момента
м подвержен действию крутящего момента 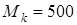 н× м. Требуется определить значения относительного и действительного углов кручения, а также наибольшее касательное напряжение в сечении стержня и значение момента инерции, если известен модуль упругости сдвига
н× м. Требуется определить значения относительного и действительного углов кручения, а также наибольшее касательное напряжение в сечении стержня и значение момента инерции, если известен модуль упругости сдвига 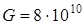 н/м2.
н/м2.
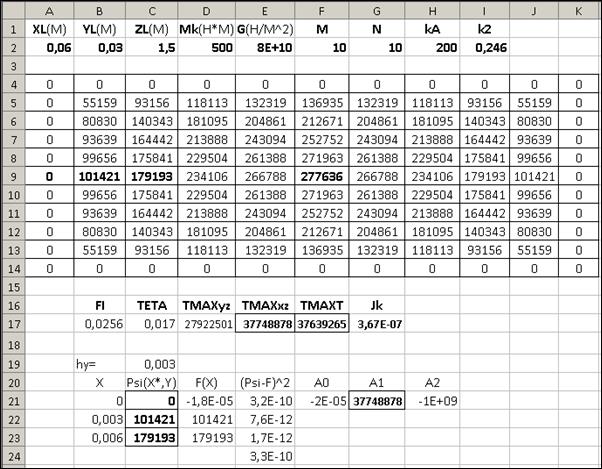
Рис. 7. 18
Входные параметры вводятся в ячейки таблицы Excel согласно рис. 7. 18. Размеры поперечного сечения 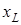 и
и 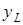 вводятся в ячейки A2 и B2; длина стержня
вводятся в ячейки A2 и B2; длина стержня 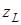 – в ячейку C2; значение крутящего момента
– в ячейку C2; значение крутящего момента 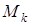 – в ячейку D2; значение модуля упругости
– в ячейку D2; значение модуля упругости 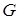 – в ячейку E2; размерности сеточной области
– в ячейку E2; размерности сеточной области 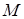 и
и 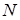 – в ячейки F2 и G2; максимальное число итераций
– в ячейки F2 и G2; максимальное число итераций 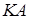 – в ячейку H2; значение коэффициента
– в ячейку H2; значение коэффициента 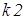 – в ячейку I2.
– в ячейку I2.
Для ввода программы, написанной на VBA, в электронную таблицу Excel следует нажать комбинацию клавиш « Alt + F11 », далее последовательно выполнить команду « Insert » и « Module. Откроется пустое окно – окно для вставки кода программы как на рис. 3. 17.
Вычисления по программе, приведенной на рис. 7. 17, привели к следующим результатам (рис. 7. 18): действительный угол кручения 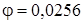 рад; относительный угол кручения (погонный угол)
рад; относительный угол кручения (погонный угол) 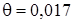 рад/м; момент инерции при кручении
рад/м; момент инерции при кручении 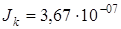 м4. На рис. 7. 19 приводится график функции напряжений Эри в прямоугольном сечении.
м4. На рис. 7. 19 приводится график функции напряжений Эри в прямоугольном сечении.
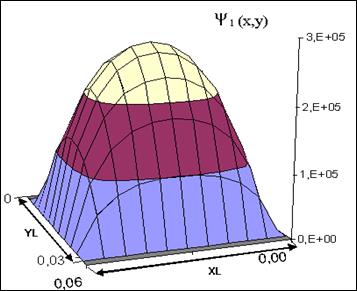
Рис. 7. 19. Функция напряжений Эри
Анализ полученных результатов (значений функции напряжений Эри  в узловых точках) показывает, что наибольшее напряжение при кручении стержня возникает в середине его сечения
в узловых точках) показывает, что наибольшее напряжение при кручении стержня возникает в середине его сечения 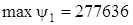 Н/м, а наибольшее касательное напряжение возникает в середине длинной стороны контура сечения (рис. 7. 20).
Н/м, а наибольшее касательное напряжение возникает в середине длинной стороны контура сечения (рис. 7. 20).

Рис. 7. 20. Касательные напряжения 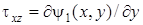 в узловых точках
в узловых точках
На рис. 7. 20 в первом приближении приводятся значения касательного напряжения 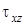 в узловых точках
в узловых точках 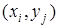 , найденные по формулам:
, найденные по формулам:
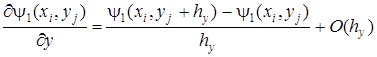 – для граничных точек (на контуре сечения) и
– для граничных точек (на контуре сечения) и
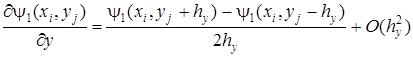 – для внутренних точек сечения.
– для внутренних точек сечения.
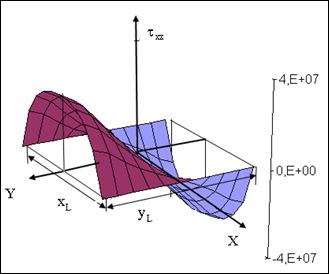
Рис. 7. 21
На рис. 7. 21 приводится график касательного напряжения 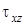 в поперечном сечении прямолинейного стержня, построенного по его значениям на рис. 7. 20.
в поперечном сечении прямолинейного стержня, построенного по его значениям на рис. 7. 20.
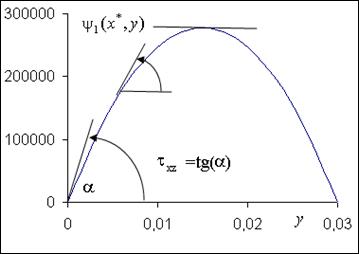
Рис. 7. 22
На рис. 7. 22 приводится линия напряжения Эри 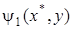 при фиксированном значении
при фиксированном значении 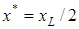 (середина длинной стороны контура сечения), где
(середина длинной стороны контура сечения), где 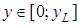 . Линия напряжения построена по результатам решения, приведенного на рис. 7. 18. Анализ показывает, что наибольшее абсолютное значение касательное напряжение
. Линия напряжения построена по результатам решения, приведенного на рис. 7. 18. Анализ показывает, что наибольшее абсолютное значение касательное напряжение 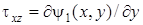 имеет в середине длинной стороны контура сечения. На рис. 7. 22 это точки при
имеет в середине длинной стороны контура сечения. На рис. 7. 22 это точки при 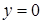 и
и 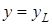 (
( 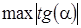 ). Таким образом, чтобы найти наибольшее абсолютное значение касательного напряжения в сечении стержня, можно интерполировать линию напряжения Эри
). Таким образом, чтобы найти наибольшее абсолютное значение касательного напряжения в сечении стержня, можно интерполировать линию напряжения Эри 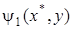 при
при 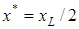 , например, по первым трем точкам из решения, приведенного на рис. 7. 18, некоторым алгебраическим полиномом. Далее можно вычислить значение производной этого полинома в начальной точке, которое можно принять за наибольшее значение касательного напряжения. Из решения, приведенного на рис. 7. 18, выбираем первые три значения
, например, по первым трем точкам из решения, приведенного на рис. 7. 18, некоторым алгебраическим полиномом. Далее можно вычислить значение производной этого полинома в начальной точке, которое можно принять за наибольшее значение касательного напряжения. Из решения, приведенного на рис. 7. 18, выбираем первые три значения 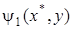 , где
, где 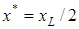 :
:
| y | 0. 003 | 0. 006 | |
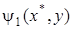
|
Далее, по выбранной таблице строится интерполяционный полином 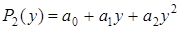 при условии
при условии 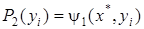 , где
, где 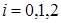 . Тогда
. Тогда 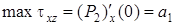 . В итоге получим расчетную формулу для определения наибольшего абсолютного значения касательного напряжения:
. В итоге получим расчетную формулу для определения наибольшего абсолютного значения касательного напряжения:
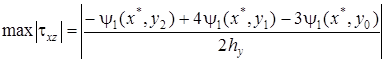 (7. 62)
(7. 62)
Для построения интерполяционного полинома также можно использовать надстройку Excel «Поиск Решения» как это показано на рис. 7. 18.
Расчеты по формуле (7. 62) привели к следующему результату (рис. 7. 18): 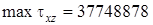 н/м2, а наибольшее значение касательного напряжения для сечения прямоугольной формы, найденное по формуле (I) из теории упругости, равно
н/м2, а наибольшее значение касательного напряжения для сечения прямоугольной формы, найденное по формуле (I) из теории упругости, равно 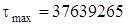 н/м2. Отклонение между этими двумя решениями незначительное, не превышает
н/м2. Отклонение между этими двумя решениями незначительное, не превышает 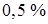 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|