Тренировочный вариант №3 профильного ЕГЭ (2022 год)

Тренировочный вариант №3 профильного ЕГЭ (2022 год)

Часть 1

1. Решите уравнение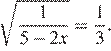

2. Аня с папой решили покататься на колесе обозрения. Всего на колесе 22 кабинки, из них 5  — желтые, 6 — белые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Аня прокатится в красной кабинке.

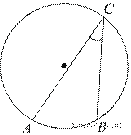
3. Найдите вписанный угол, опирающийся на дугу, которая составляет 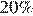окружности. Ответ дайте в градусах.

4. Найдите значение выражения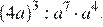 

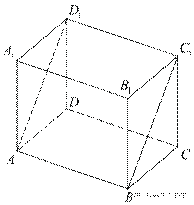
5. В прямоугольном параллелепипеде 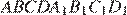известны длины рёбер:

Найдите площадь сечения параллелепипеда плоскостью, проходящей через точк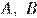и и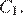

6. На рисунке изображен график производной функции определенной на интервале 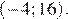Найдите количество точек максимума функции 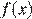на отрезке

7. Для сматывания кабеля на заводе используют лебeдку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со временем по закону 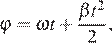где t  — время в минутах,  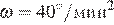 — начальная угловая скорость вращения катушки, а  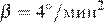 — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки достигнет 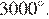Определите время после начала работы лебeдки, не позже которого рабочий должен проверить еe работу. Ответ выразите в минутах.

8. Два человека отправляются из одного дома на прогулку до опушки леса, находящейся в 1, 1  км от дома. Один идёт со скоростью 2, 5  км/ч, а другой  — со скоростью 3  км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча? Ответ дайте в километрах.

9. На рисунке изображён график функции вида 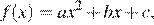где числа a,   b и c  — целые. Найдите значение дискриминанта уравнения .

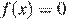10. Биатлонист 3 раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0, 8. Найдите вероятность того, что биатлонист первые 2 раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых.

11. Найдите точку максимума функции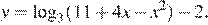

Часть 2

12. а) Решите уравнение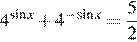

б) Укажите корни этого уравнения, принадлежащие отрезку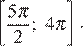

13. Дана правильная треугольная призма АВСА₁В₁С₁, все рёбра которой равны 6. Через точки A, С₁ и середину T ребра А₁В₁ проведена плоскость.

а) Докажите, что сечение призмы указанной плоскостью является прямоугольным треугольником.

б) Найдите угол между плоскостью сечения и плоскостью ACC₁.

14. Решите неравенство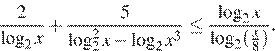

15. В июле планируется взять кредит на сумму 1 342 000 рублей. Условия его возврата таковы:

— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить некоторую часть долга.

На сколько рублей больше придётся отдать в случае, если кредит будет полностью погашен четырьмя равными платежами (то есть за 4 года), по сравнению со случаем, если кредит будет полностью погашен двумя равными платежами (то есть за 2 года)?

16. Точка E  — середина боковой стороны CD трапеции ABCD. На стороне AB взяли точку K так, что прямые CK и AE параллельны. Отрезок CK и BE пересекаются в точке O.

а) Доказать, что CO = KO.

б) Найти отношение оснований трапеции BC и AD, если площадь треугольника BCK составляет 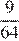площади трапеции ABCD.

17. Найдите все значения x, каждое из которых является решением уравнения 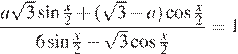при любом значении a из отрезка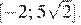

18. Вася и Петя решали задачи из сборника, причем каждый следующий день Вася решал на одну задачу больше, чем в предыдущий, а Петя  — на две задачи больше, чем в предыдущий. В первый день каждый решил хотя бы одну задачу, а в итоге каждый решил все задачи сборника.

а) Могло ли быть в сборнике 85 задач?

б) Могло ли быть в сборнике 213 задач, если каждый из мальчиков решал их более трех дней?

в) Какое наибольшее количество дней мог решать задачи Петя, если Вася решил весь сборник за 16 дней, а количество задач в сборнике меньше 300.