
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Приложение 4
Практическое занятие 8. Потери напора при движении жидкости
Основные теоретические положения.
8. 1. Потери напора на трение.
Потери напора на трение вдоль потока жидкости, которые возникают при равномерном напорном движении жидкости в трубах, определяют по формуле Дарси-Вейсбаха, которая является универсальной:
һ тр=λ ∙ l/d∙ v2/2g, м (8. 1)
где l – длина участка трубопровода, м;
d – внутренний диаметр трубопровода, м;
v – средняя скорость потока, м/с;
g – ускорение свободного падения, м/с2;
λ – безразмерный коэффициент гидравлического трения.
Теория гидродинамического подобия говорит о том, что λ должен быть функцией числа Re, а также может зависеть от безразмерного геометрического фактора D/d, где D - шероховатость стенок трубопровода.
Абсолютной шероховатостью D называют высоту неровностей – выступов на внутренних поверхностях трубопровода.
Значение эквивалентной шероховатости Dэ для некоторых труб приведена в приложении 3. При турбулентном режиме шероховатость стенок существенно влияет на сопротивление движению жидкости, потому что способствует турбулизации потока.
Потери давления на трение по длине трубопровода определяют по формуле:
∆ Ртр=λ ∙ l/d∙ ρ ∙ v2/2, Па, (8. 2)
где ρ – плотность жидкости, кг/м3.
8. 1. 1. Потери напора на трение при ламинарном режиме.
Закон гидравлического сопротивления при ламинарном режиме, установлен экспериментально Ж. Пуазейлем и имеет математическое выражение:
һ тр=(32 ∙ l ∙ ν ∙ v )/(g ∙ d2 ) (8. 3)
Из формулы выходит, что потери на трение при ламинарном режиме пропорциональны первой степени скорости (что согласуется с опытами Рейнольдса). Кроме этого шероховатость стенок не проявляет влияния на потери напора.
То есть при ламинарном режиме потери напора могут быть определены по формулам как (8. 1), так и (8. 3).
Следует обратить внимание на то, что коэффициент гидравлического трения λ для ламинарного режима движения имеет практически постоянное значение
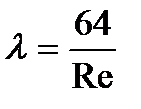 . (8. 4)
. (8. 4)
8. 1. 2. Потери напора на трение при турбулентном режиме.
В турбулентном режиме потери напора обусловлены перемешиванием конечных масс жидкости и появлением в связи с этим дополнительного напряжения трения, а потому они пропорциональны квадрату скорости.
Рассмотрим некоторые данные, полученные. Никурадзе (рис. 4. 1). Он исследовал сопротивление трубопроводов с равномерной зернистой искусственной шероховатостью. Из графических данных следует, что зависимость коэффициента сопротивления трения по длине трубопровода от числа Re может быть разделена на четыре зоны.
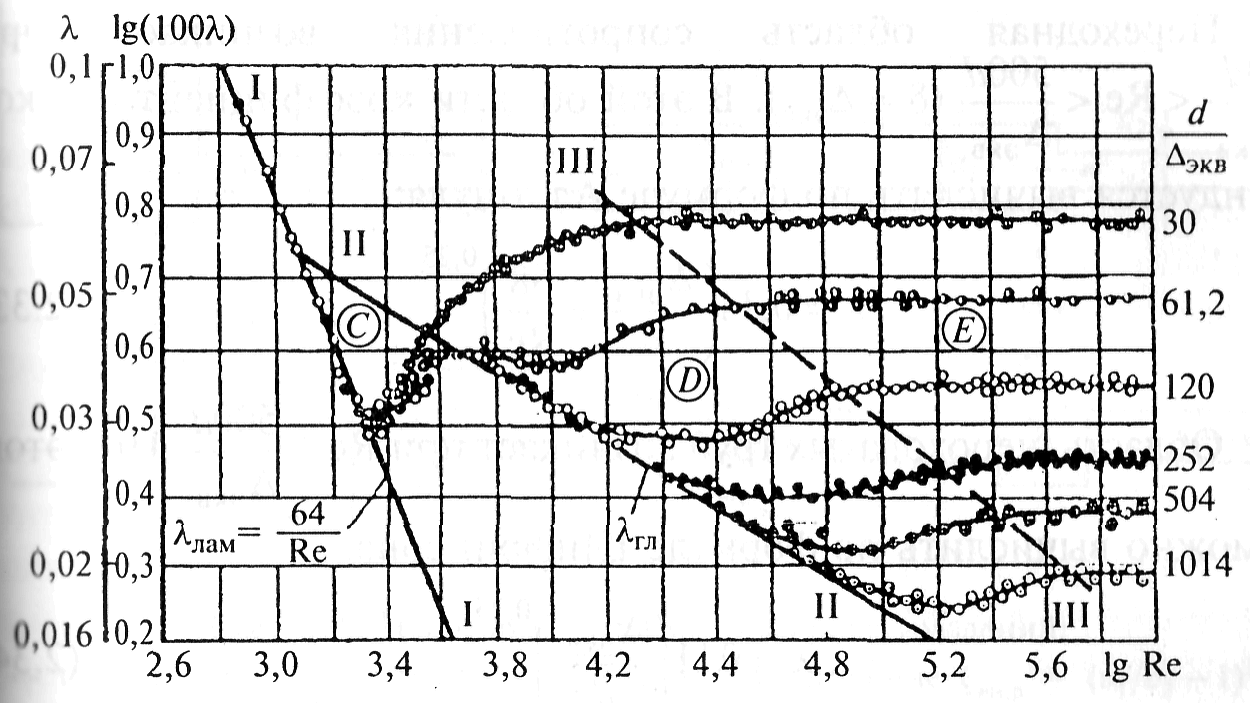
Рис. 8. 1 График И. Никурадзе – зависимость λ =f(Re, d/∆ экв ) для труб с однородной ровнозернистой шероховатостью:
I – зона ламинарного режима; II – переходная зона; III – зона турбулентного режима; С – область гидравлически гладких труб; D – зона к квадратичной области сопротивления; Е – квадратичная область сопротивления.
Первая зона относится к ламинарного режима. Здесь l является функцией только числа Re и определяется зависимостью l=64/Re.
Во второй зоне закономерности, которым подчиняется l, неоднообразно. Так, при Re > 2320 до Re » 4000, движение жидкости характеризуется сложным законом гидравлического сопротивления. Потери напора практически не зависят от шероховатости труб. Для этой области течения величина коэффициента сопротивления трения может быть определена зависимостью, полученной Н. И. Френкелем.
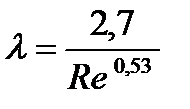 (8. 5)
(8. 5)
При турбулентном режиме движения, когда Re > 4000, различают зону гидравлически гладких труб С, которая входит во вторую. Для определения l в пределах данного участка кривой можно пользоваться формулами:
Блазиуса 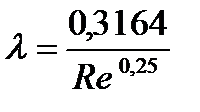 при 4000 < Re < 105 (8. 6)
при 4000 < Re < 105 (8. 6)
Колбрука – Конакова 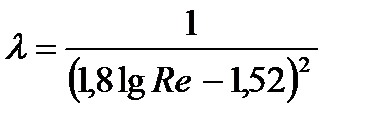 при 4000 < Re < 106. (8. 7)
при 4000 < Re < 106. (8. 7)
Эти формулы используются для расчета технически гладких труб, к которым относят стеклянные, цельнотянутые трубы из цветных металлов (а также из алюминиевых сплавов) и высококачественные бесшовные стальные трубы. К технически гладким трубам относят также топливопроводы и трубы, которые используют в гидросистемах.
Зона D – доквадратичного сопротивления. В этой области турбулентного движения для не вполне шероховатых труб потери напора определяются числом Re и шероховатостью стенок трубы.
Ориентированно границы зоны определяются неравенством
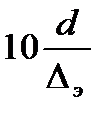 < Re <
< Re < 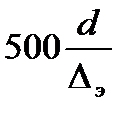
Численные значения Dэ для труб из различных материалов приводятся в справочной литературе.
Для этой области течения можно использовать ряд зависимостей:
формула Кольбрука
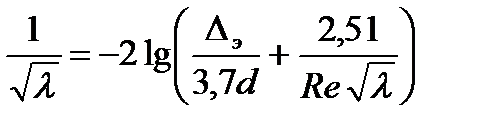 (8. 8)
(8. 8)
формула А. Д. Альтшуля
λ =0, 1((1, 46 ∙ ∆ э)/d+ 100/Re)0, 25 ≈ 0, 11 (( ∆ э)/d+ 68/Re)0, 25. (8. 9)
Рассмотрим зону Е, где сопротивление пропорционально квадрату скорости, то есть зону квадратичного сопротивления, “вполне шероховатых” труб. Нижней чертой зоны является неравенство Re > 500 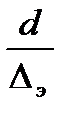 (справа от условной линии). Здесь потери напора и коэффициент сопротивления трения по длине l зависят от гладкости d/ Dэ, а от Re не зависят. Поэтому графики, которые определяют величину l для квадратного сопротивления, представляет собой прямые линии, параллельные оси абсцис.
(справа от условной линии). Здесь потери напора и коэффициент сопротивления трения по длине l зависят от гладкости d/ Dэ, а от Re не зависят. Поэтому графики, которые определяют величину l для квадратного сопротивления, представляет собой прямые линии, параллельные оси абсцис.
Для определения l в этой зоне предложены ряд формул. К наиболее известным относятся:
Прандтля – Никурадзе 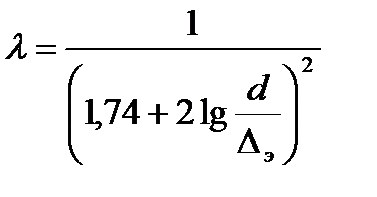 , (8. 10)
, (8. 10)
Шифринсона 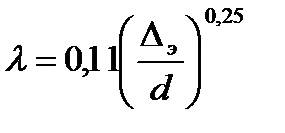 (8. 11)
(8. 11)
Павловского и другие.
Исследования показали, что квадратичный закон сопротивления подтверждается далеко не во всех случаях движения жидкости. Однако формула Дарси-Вейбаха оказалась очень удобной для практических целей и целесообразной с точки зрения единообразия расчета и обычно используется как для ламинарного, так и для турбулентного режима. Отклонения от квадратичного закона учитываются тем, что значение коэффициента l ставится в посредственную зависимость от скорости.
В дальнейшем в следствие многочисленных опытов с техническими трубопроводами, то есть с трубами, шероховатость стенок которых обуславливалась естественными условиями, было выявлено следующее. Во-первых, рабочей для технических трубопроводов является главным образом переходная область сопротивления. Во-вторых, закономерность изменения сопротивления в переходной области по сравнению с трубами, имеющими искуственную шероховатость, носит совсем иной характер: для технических трубопроводов l растет вместе с уменьшением Re, при чем l имеет большее абсолютное значение.
Г. А. Муриным были проведены и обработаны опыты по исследованию труб различных сортаментов диаметром от 40 до 160 мм.
Результаты опытов предоставлены графику (рис. 8. 2) в пределах Re = 4× 10-3 … 4× 107. Здесь четко различаются три области сопротивления при турбулентном режиме.
S rpLaYZ/gppWzLFtIgw2nhRo7OtRU3s53oyBWx+IrlvOC99+fGB+Hi+sXF6Xex8NuBSLQEF7hZ/uo Fczh/0q6AXLzBwAA//8DAFBLAQItABQABgAIAAAAIQDb4fbL7gAAAIUBAAATAAAAAAAAAAAAAAAA AAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsBAi0AFAAGAAgAAAAhAFr0LFu/AAAAFQEAAAsAAAAA AAAAAAAAAAAAHwEAAF9yZWxzLy5yZWxzUEsBAi0AFAAGAAgAAAAhABViGtjBAAAA2gAAAA8AAAAA AAAAAAAAAAAABwIAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAAAwADALcAAAD1AgAAAAA= "> 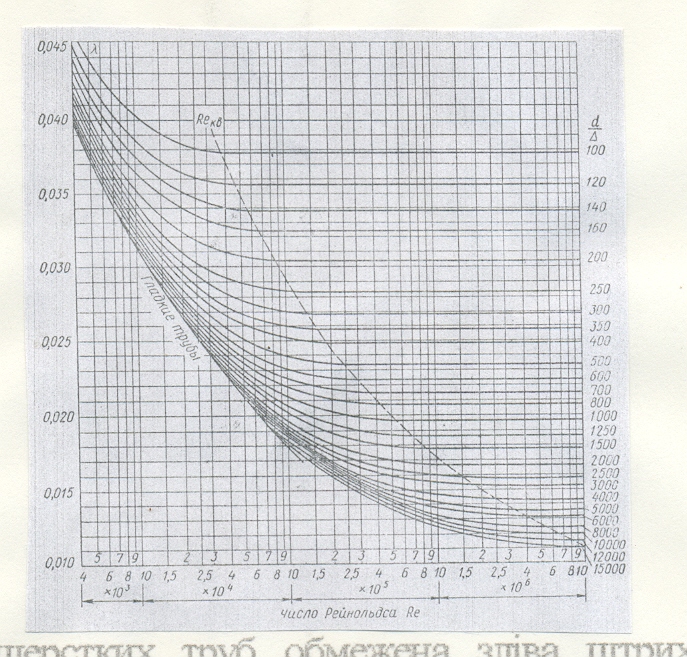
Рис. 8. 2 График Г. А. Мурина
Область шероховатых труб ограничена слева штриховой линией. Линии l= f(Re) параллельны оси абсцисс и коэффициент гидравлического сопротивления определяется только шероховатостью стенок трубы. Переходная область сопротивления ограничивается справа штриховой линией, а слева – огибающей кривой. Значение l зависят не только от шероховатости, но и существенно возрастает с уменьшением числа Re.
Сводная таблица расчетных формул для определения коэффициента гидралического трения λ приведена в приложении 4.
8. 1. 2. Потери напора в местных сопротивлениях
Местные потери напора вызываются сопротивлениями в арматуре, фасонных частях и оборудовании, вследствие сужения и расширения потока, изменения направления движения жидкости, слияния и разделения потока и тому подобное
Потери на преодоление местных сопротивлений в наружных сетях водопровода обычно не превышают 10-15%, во внутренних сетях – 30% от потерь напора по длине.
Однако местные потери напора в некоторых видах инженерных сетей могут достигать значительной величины: так, например, в системах отопления зданий – до 40%, в воздуховодах вентиляционных систем и пневмотранспорте – до 60-70% от потерь напора по длине.
Местные потери напора определяют как скоростной напор непосредственно вблизи местного сопротивления ξ по формуле Вейсбаха:
hмест. сопр= ξ ∙ V2/2g (8. 12)
Общей теории для определения коэффициентов местных сопротивлений, за исключением отдельных случаев, нет. Поэтому коэфициенты местных сопротивлений, находят опытным путем. Значения их для разных элементов трубопроводов приводятся в технических справочниках. Так, в приложениях 6 и 7 приведены значения коэффициентов ξ некоторых местных сопротивлений, и запорных устройств трубопроводов.
Примеры решения задач.
8. 1. Определить потери напора на трение вдоль трубопровода диаметром d = 20 мм и длиной l = 500 м при движении в нем воды с расходом Q = 2, 5∙ 10-5 м3/сек. Температура воды 200С.
Решение.
Определим скорость движения жидкости в трубопроводе. Средняя скорость определяется из уравнения постоянства расхода (1. 1):
v= Q/F= (4∙ Q)/(π ∙ d2 )= (4 ∙ 2, 5∙ 10-5)/(3, 14 ∙ 0, 022 )=0, 0796 м/сек.
Число Рейнольдса Re определяется по формуле (3. 1). Значение коэффициента кинематической вязкости, принимаем из приложения 1. Итак:
Re= (v∙ d)/ν = (0, 0796 ∙ 0, 02)/(1, 01∙ 10-6)=1576.
Полученное значение числа Рейнольдса Re < Reкр = 2320, поэтому режим движения воды в трубопроводе – ламинарный. Потери напора на трение определим с помощью формулы Пуазейля (4. 3):
һ тр=(32 ∙ l ∙ ν ∙ v)/(g ∙ d2 )= (32 ∙ 500 ∙ 1, 01∙ 10-6 ∙ 0, 0796)/(9, 81 ∙ 0, 022 )=0, 327 м.
8. 2. Вентиляционная труба d = 100 мм имеет длину l = 100 м (∆ экв = 0, 2 мм). Определить давление, которое должен развивать вентилятор, если расход воздуха в трубопроводе Q = 0, 078 м3/сек. Давление на выходе Р = Ратм = 101 кПа. Местных сопротивлений трубопровод не имеет. Температура воздуха 200С.
Решение.
Определим скорость движения воздуха в трубопроводе по формуле (1. 1):
v= Q/F= (4∙ Q)/(π ∙ d2 )= (4 ∙ 0, 078)/(3, 14 ∙ 0, 12 )=10 м/сек.
Число Рейнольдса (3. 1) для потока воздуха в трубе при υ = 15, 7 ∙ 10-6 м2/с:
Re= (v∙ d)/ν = (10 ∙ 0, 1)/(15, 7∙ 10-6)=69 000.
Коэффициент гидравлического трения определим по формуле Альтшуля (8. 9):
λ =0, 11( ∆ э/d+ 68/Re)0, 25=0, 11( 0, 2/100+ 68/69000)0, 25=0, 0256.
Используя формулу (8. 2) определим потери давления на трение (ρ воздух = 1, 18 кг/м3):
∆ Ртр=λ ∙ l/d∙ ρ ∙ v2/2=0, 0256 ∙ 100/0, 1∙ 1, 18∙ 102/2=1510, 4 Па=1, 51 кПа.
8. 3. Задания для самостоятельной работы.
8. 3. 1. Рассчитать потери давления в прямом трубопроводе, длина которого l = 40 м и внутренний диаметр которого d = 16 мм при движении в нем жидкости, плотностью ρ = 890 кг/м3 и вязкостью ν = 20∙ 10-6 м2/сек. Скорость потока 2 м/сек.
8. 3. 2. По прямой трубе, длина которой 100 м и диаметр которой d = 100 мм протекает жидкость с объемным расходом Q = 5 л/с, которая имеет кинематическую вязкость ν = 0, 4∙ 10-4 м2/с. Определить потери напора по длине.
8. 3. 3. Определить потери напора на трение по длине в новом стальном трубопроводе Δ э= 0, 1 мм, диаметром d = 200 мм и длиной 2 км, если по нему транспортируется вода с расходом Q = 20 л/сек. Кинематическая вязкость воды
ν = 1, 01∙ 10-6 м2/сек.
8. 3. 4. По прямой трубе длиной l = 1 км, диаметром d = 100 мм протекает со средней скоростью v = 0, 4 м/с жидкость, которая имеет кинематическую вязкость ν = 1, 01∙ 10-6 м2/сек Определить потерю напора на трение hr.
8. 3. 5. По горизонтальному трубопроводу, который имеет диаметр d = 203 мм и длину l = 24 км, перекачивается мазут (ρ = 850 кг/м3 и вязкостью ν = 1, 01∙ 10-6 м2/с). Определить весовой расход G, если давление, которое развивается насосами, р1 = 10, 5 ат, а конечное давление р2 = 1 ат.
8. 3. 6. Определить суточную пропускную способность самотечного нефтепровода диаметром d = 203 мм при движении по нему нефти (ρ = 900 кг/м 3, ν = 1, 46∙ 10-6 м2/с). Длина трубопровода l = 10 км и начальная точка находится выше на конечную ∆ h= 50 м.
8. 3. 7. Определить потерю напора hr и гидравлический уклон i при перекачке G = 70 т/ч мазута (ρ = 930 кг/м3 ), вязкостью ν = 1, 5∙ 10-6 см2/с по трубопроводу диаметром d = 156 мм, длиной l =5 км.
8. 3. 8. При перекачке керосина (ρ = 820 кг/м3 ) по трубопроводу диаметром d = 100 мм в количестве G = 535 т/сут определялся гидравлический уклон, равный i = 0, 00821. Найти коэффициент гидравлического сопротивления λ.
8. 3. 9. Определить потерю напора hr в трубопроводе диаметром d = 257 мм, длиной l =1000 м при ∆ экв = 0, 15 мм, если весовая масса нефти, которая перекачивается по этому трубопроводу, G = 200 т/ч, плотность нефти ρ = 880 кг/м3 и вязкостью ν = 0, 276 см2/сек. Обосновать выбор расчетной формулы.
8. 3. 10. По горизонтальному трубопроводу длиной l =40 км и диаметром d = 203 мм (∆ экв = 0, 15 мм ) перекачивается вода при температуре t = 20оС в количестве Q = 90 м3/час. Определить перепад давления ∆ р и потери напора по длине.
8. 3. 11. Из резервуара по горизонтальной трубе диаметром d = 50 мм и длиной l =20 м вытекает в атмосферу вода. Уровень воды над осью трубы Н = 4 м поддерживается постоянным. Определить расход воды Q, пренебрегая местными сопротивлениями и принимая (в первом приближении) коэффициент сопротивления λ = 0, 03.
Приложение 3
Значения еквивалентной шероховатости труб
| Труби, их материал и состояние | ∆ э, мм |
| Цельнотянутые трубы | |
| Нові технічні гладкі з скла, латуні, міді, свінца | 0, 0015…0, 01 |
| Те саме з алюмінію | 0, 015…0, 06 |
| Сталеві нові | 0, 02…0, 05 |
| Сталеві після декількох років експлуатації, очищенні та бітумінізовані | 0, 15…0, 3 |
| Стальные сварные трубы | |
| Нові | 0, 04…0, 1 |
| Що були в експлуатації | 0, 1…0, 15 |
| Помірно заржавлені | 0, 3…0, 7 |
| Старі поржавілі | 0, 8…1, 5 |
| Сильно поржавілі з великими відхиленнями | 2…4 |
| Оцинкованнные стальные трубы | |
| Нові чисті | 0, 07…0, 15 |
| Оцинковані з листової сталі нові | 0, 15 |
| Те саме, які були в експлуатації | 0, 18 |
| Чугунные трубы | |
| Нові | 0, 25…1, 0 |
| Нові бітумінізовані | 0, 12…0, 3 |
| Що були в експлуатації | 1, 0…1, 5 |
| Зі значними відкладеннями | 2…4 |
| Очищені, після багатьох років експлуатації | 0, 3…1, 5 |
| Сильно поржавілі з великими відхиленнями | до 3 |
| Бетонные и другие трубы | |
| Бетонні, нормальна поверхня з затіркою | 0, 3…0, 8 |
| Те саме при середньої якості робот; залізобетонні | 2, 5 |
| Те саме при шороховатій поверхні | 3…9 |
| Асбестоцементні нові | 0, 05…1 |
| Те саме, які були в експлуатації | 0, 6 |
| Скляні | 0, 0015…0, 1 |
| Рукава і шланги гумові | 0, 03 |
Приложение 4
Сводная таблица формул для расчета коэффициента гидравлического трения λ
| Область гідравлічної зони | Розрахункові формули |
| Re < 2300 | 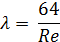
|
| від Re > 4000 до Re < 10 ∙ d/Δ екв | Формула Блазіуса
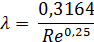 Формула Конакова
λ = (1, 8 ∙ lg Re – 1. 5) -2
Формула Нікурадзе
Формула Конакова
λ = (1, 8 ∙ lg Re – 1. 5) -2
Формула Нікурадзе
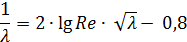
|
| від Re > 10 ∙ d/Δ екв до Re < 500 ∙ d/Δ екв | Формула Альтшуля
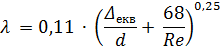
|
| Re > 500 ∙ d/Δ екв | Формула Шифрінсона 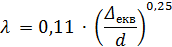 Формула Нікурадзе
Формула Нікурадзе
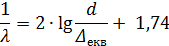
|
| Без обмежень | Формула Кольбрука – Уайта
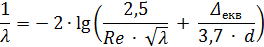 Формула Альтшуля
Формула Альтшуля
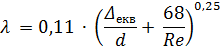
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|