Урок 60. Об аксиомах планиметрии

8. 05. 2020.

Урок 60. Об аксиомах планиметрии

Цель	Создать условия для организации и проведения закрепления знаний учащихся об основных аксиомах планиметрии
Изучение новой темы
Цель деятельности	Ход урока
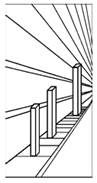
Рассмотреть основные аксиомы стереометрии	– Что такое геометрия? – Какой раздел геометрии мы изучали в 7–9 классах? (Планиметрия. ) – Какой еще раздел геометрии вы знаете? (Стереометрия. ) Что он изучает? – Изучение стереометрии важно, именно она дает необходимые пространственные представления, знакомит с законами восприятия и изображения пространственных фигур, что позволяет человеку ориентироваться в окружающем мире. Пример 1. (Из книги И. М. Фейгенберга «Видеть – предвидеть – действовать»). Рассмотрите рисунки. Что вы видите на них? 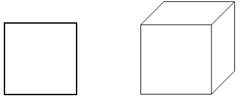Пример 2. Что изображено на рисунках? С таким изображением куба очень трудно работать: не все элементы видны. – Для того чтобы правильно изображать пространственные фигуры и решать геометрические загадки, необходимо знать и уметь применять аксиомы планиметрии. Аксиома – греческое слово, означающее «достойная признания». Это факты, которые принимаются без доказательства. Остальные утверждения доказываются и называются теоремами, следствиями, свойствами и признаками. Рассматрите аксиомы 1, 2 на с. 337. – Сформулируйте 3-ю аксиому планиметрии. (Через любые две точки можно провести прямую, и притом только одну. Из трех точек прямой одна и только одна лежит между двумя другими. ) – Плоскости обозначают греческими буквами α, β, . – Наряду с точкой, прямой и плоскостью в планиметрии рассматривают геометрические тела, изучают их свойства, измеряют их площади и объемы. Рассматриваются такие случаи, когда не все точки, линии и углы данной или данных фигур будут располагаться на одной плоскости. Прочитайте по учебнику с. 337–341
Закрепление изученного материала
На простейших задачах отработать понимание аксиом стереометрии	1. Решить задачи устно. 1) Три мухи разлетелись в разные стороны. При каких условиях все они окажутся в одной плоскости? (Аксиома 1. ) 2) Угольный пласт обычно залегает так, что его верхняя граница представляет собой часть плоскости. Какое наименьшее число скважин следует прорубить для того, чтобы определить, как расположен пласт? (Аксиома 1. ) 3) Постройте в тетрадях изображение куба АВСDА₁В₁С₁D₁. (Фото мне) 4) вар из ОГЭ см ниже. Мне полные решения, а не голые ответы.
Домашнее задание:		Вар из ОГЭ см ниже Мне полные решения, а не голые ответы.

кл. работа

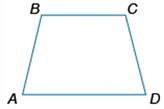
16. В равнобедренной трапеции ABCD меньшее основание BC равно 5 см, боковая сторона — 4 см, а угол при основании равен — 60∘. Найдите большее основание AD (в см).

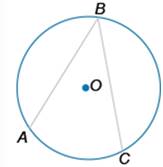
17. В окружности с центром в точке O проведены две хорды AB и BC. Дуга ABC равна 280∘. Найдите угол ABC (в градусах).

18. Найдите площадь равнобедренного треугольника (в см²) высота которого, проведенная к основанию, равна 8 см, а боковая сторона — 10 см.

19. Найдите синус угла BAC, изображённого на рисунке.

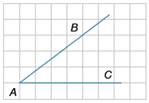
20. Укажите номера неверных утверждений.

1) Развёрнутый угол больше 180∘

2) В треугольнике может быть только один тупой угол.

3) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники равны.

4) В равнобедренном треугольнике высота, проведённая к основанию, является медианой.

Дом. задание.

16. В равностороннем треугольнике ABC проведена медиана AM. Сторона AB=10 см. Чему равен отрезок MB (в см)?

17. В четырехугольник ABCD вписана окружность. Периметр четырехугольника равен 120 см, сторона CD=20 см. Найдите сторону AB. Ответ дайте в см.

18. Найдите площадь трапеции, средняя линия которой равна 6 см, а высота — 5 см. Ответ дайте в см²

19. Найдите тангенс угла ABC, изображённого на рисунке.

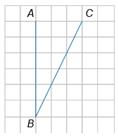
20. Укажите номера верных утверждений.

1) Диагонали ромба равны.

2) Любой прямоугольник является параллелограммом.

3) Косинус угла в треугольнике всегда меньше синуса.

4) Все высоты треугольника пересекаются в одной точке.